４　正四面体群
f-denshi.com  最終更新日：　04/02/29
［目次へ］
サイト検索

　この章からは正四面群を例に取り上げ，部分群のもつ性質，特にその対称性について掘り下げていきます。２次元図形の正六角形から３次元図形の正四面体なることでちょっと手強くなります。まず，この章では正四面体群を定義し，正四面体の各頂点につけられた番号の置換に着目した表現方法を示します。



１．正四面体群の元

変換
⇒
a1
サイトの番号 変換前の頂点 変換後の頂点

［１］　正四面体群 （しばしば「P４」（＝交代群A4）と書く） とは正四面体をそれ自身に重ね合わせるような３元空間内での回転操作（これを変換と呼びます）の全体を元とする回転群です。そのような変換は正四面体をまったく動かさない恒等変換を含めて，12個あります。まず最初に，正四面体の各頂点につけられた番号が回転によってどう移るかを利用して12個の元を識別する名前を付けましょう。

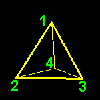
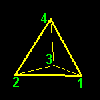
［２］　まず，回転によらない絶対的な空間の位置を示すのに1，2，3，4と右のような空間の位置（＝サイト）に番号を付けます。そして，その順に1，2，3，4と番号のついた頂点が対応するように正四面体を置く ”置き方” を ”変換前の配置”＝”恒等変換” とします。

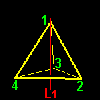
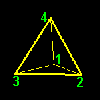
［３］　この正四面体を頂点１から対する面（＝三角形234）におろした垂線L1の周りに頂点１から見て反時計回りに120度回転させるともとの正四面体と重なることがわかります（上図/右端）。よって，この回転操作（a1と呼びましょう）は正四面体群P4の元であることがわかります。　これを a1 と書くことにしましょう。

［４］この変換a1によって，もともとの頂点1，2，3，4の位置が回転後，回転前の頂点の位置1，3，4，2にそれぞれ移っていることに注目しましょう。すると，この変換は置換：

　a1＝ 1 2 3 4 　≡　［1342］　←変換後の頂点1，2，3，4 の収まるサイトの番号と思ってください。
1 3 4 2

変換後の正四面体の頂点の位置　
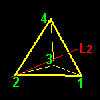
a1＝［1342］ b1＝［1423］ a2＝［4213］ b2＝［3241］
頂点１の周りの回転 頂点２の周りの回転
　

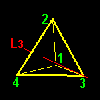
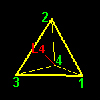
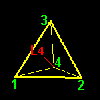
a3＝［2431］ b3＝［4132］ a4＝［3124］ b4＝［2314］
頂点３の周りの回転 頂点４の周りの回転
　　
hx＝［3412］ hy＝［2143］ hz＝［4321］ e＝［1234］
対辺中心 の 周 り の 回 転 恒等変換

に対応させることができます。［　］はこのサイトだけの略記法です。

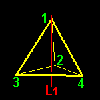
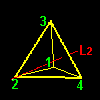
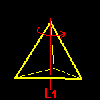
　　このようなタイプの変換は右図のような各頂点を通る４本の回転軸L1，L2，L3，L4のまわりに左右回り２つつずつ，合計８個存在します。頂点 j から見て120度の反時計回り（正方向120度）を aj ，120度の時計回り（正方向240度）を bj  と名前を付けておきましょう。置換［ ］の記号で書くと

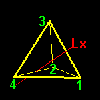
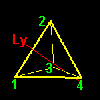
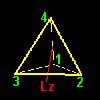
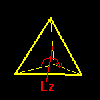
a1＝［1342］，b1＝［1423］，　：頂点１周りの回転
a2＝［4213］，b2＝［3241］，　：頂点２周りの回転
a3＝［2431］，b3＝［4132］，　：頂点３周りの回転
a4＝［3124］，b4＝［2314］，　：頂点４周りの回転
［５］　２番目のタイプとしては，相対する２つの辺の中点を通る回転軸 Lx，Ly，Lzのまわりの180度の回転（右下図）で，例えば，Lx回りの回転は1と3，および2と4の互換を同時に行なうような置換になっています。置換記号で書くと，
hx＝［3412］　：辺１３と辺２４の中点と結ぶ回転軸Lx
hy＝［2143］　：辺１２と辺３４の中点と結ぶ回転軸Ly
hz＝［4321］　：辺１４と辺２３の中点と結ぶ回転軸Lz
の３つとなります。

［６］　最後，何もしない変換も恒等変換を，

e＝［1234］

としてこれも元に含めなければ群をなしません。

以上，12個が正四面体群の元となります。といってもまだ演算を定義する必要がありますが，・・・。

２．演算

［１］　正四面体群P4の元の間に定義される演算　”・”　は，

「　演算：二つの回転を続けておこなうこと　」

と定義します。たとえば，回転 b2 をおこない，引き続いて回転 a1 をおこなうことは上の図を参照して頂点動き方を追いかければ，回転 hz に等しいことがわかります。

⇒ ⇒ ←
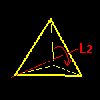b2 a1 hz
変換前 変換後 変換前

同じことですが，これはすでに定義してある置換の積を計算して，

a1・b2＝［1342］・［3241］＝ 1 2 3 4 1 2 3 4 ＝ 1 2 3 4 ＝［4321]＝hz
1 3 4 2 3 2 4 1 4 3 2 1

のように求めることもできます。

いずれかの方法で１２×１２＝１４４個の積すべてを求めて表にすると正四面体群の群表（＝積表）は下のようになります。

X･Y e a1 b1 a2 b2 a3 b3 a4 b4 hx hy hz
e e a1 b1 a2 b2 a3 b3 a4 b4 hx hy hz
a1 a1 b1 e b4 hz b2 hy b3 hx a2 a4 a3
b1 b1 e a1 hx a3 hz a4 hy a2 b4 b3 b2
a2 a2 b3 hz b2 e b4 hx b1 hy a1 a3 a4
b2 b2 hx a4 e a2 hy a1 hz a3 b3 b4 b1
a3 a3 b4 hy b1 hx b3 e b2 hz a4 a2 a1
b3 b3 hz a2 hy a4 e a3 hx a1 b2 b1 b4
a4 a4 b2 hx b3 hy b1 hz b4 e a3 a1 a2
b4 b4 hy a3 hz a1 hx a2 e a4 b1 b2 b3
hx hx a4 b2 a3 b1 a2 b4 a1 b3 e hz hy
hy hy a3 b4 a4 b3 a1 b2 a2 b1 hz e hx
hz hz a2 b3 a1 b4 a4 b1 a3 b2 hy hx e

正四面体群表　

これで第一段階の準備完了です。

［２］　この群の位数は12ですが，生成元は5つで，たとえば，e，a1，hx，hy，hz　と選べます。つまり，

A4＝<e，a1，hx，hy，hz>

この表のa1の行を見れば，生成元　a1とhx，hy，hz　との積から，b1とa2，a3，a4　が得られ，さらにa2，a3，a4 の二乗からb2，b3，b4 が得られるからです。

（↑この表を完成させるのは結構疲れます。しかし，群論はこのような表を自分でいくも作ってみないことには理解が深まりません。）

［目次へ］

x∈A4 の互換，巡回置換を用いた表示
e e a1 (234) b1 (243)
hx (13)(24) a2 (143) b2 (134)
hy (12)(34) a3 (124) b3 (142)
hz (14)(23) a4 (132) b4 (123)