
| 14 剰余類の乗法群 |  |
|
| f-denshi.com 最終更新日: | ||
| [目次へ] | ||
| サイト検索 | ||
[1] 整数の剰余類の集合Znについては,[a]n に属する任意の元 a’および,[b]n に属する任意の元 b’とすると,
a≡a’ (mod n), b≡b’ (mod n) → a×b ≡ a’× b’ (mod n)
となります。なぜなら,整数 c,d を用いて,a−a’= c×n, b−b’= d×n とおくと,
| a×b=(a’+c×n)(b’+d×n) = a’× b’ + | (a’×d+b’×c+c×d×n) | ×n |
| 整数 |
となるからです。したがって,11.の加法と同様に,剰余類の乗法(積)を
[a]n × [b]n=[a× b]n
によって定義し,演算に意味をもたせることができます。
[2] この積をもとでのZ5の各元の演算結果を表(乗積表)にしてみると,
× [0]5 [1]5 [2]5 [3]5 [4]5 [0]5 [0]5 [0]5 [0]5 [0]5 [0]5 [1]5 [0]5 [1]5 [2]5 [3]5 [4]5 [2]5 [0]5 [2]5 [4]5 [1]5 [3]5 [3]5 [0]5 [3]5 [1]5 [4]5 [2]5 [4]5 [0]5 [4]5 [3]5 [2]5 [1]5
となり,[0]5の関係した部分を除いた部分(色の濃い部分)は群を作っていることがわかります。すなわち,
| 定理: Z5* ≡ (Z/5Z)* =Z5−{[0]5} = {[1]5,[2]5,[3]5,[4]5} は乗法×のもとで群をなす。 |
ことがわかります。単位元は[1]5 であり,逆元の存在もすべての行,(列)に[1]5 が存在することからわかります。
[3] しかし,どんな n についても Zn* が乗法群をなすわけではありません。たとえば,Z6 の乗法表を作ると,
× [0]6 [1]6 [2]6 [3]6 [4]6 [5]6 [0]6 [0]6 [0]6 [0]6 [0]6 [0]6 [0]6 [1]6 [0]6 [1]6 [2]6 [3]6 [4]6 [5]6 [2]6 [0]6 [2]6 [4]6 [0]6 [2]6 [4]6 [3]6 [0]6 [3]6 [0]6 [3]6 [0]6 [3]6 [4]6 [0]6 [4]6 [2]6 [0]6 [4]6 [2]6 [5]6 [0]6 [5]6 [4]6 [3]6 [2]6 [1]6
となり,Z6* は群をなしません。[2]6,[3]6,[4]6に逆元が存在しないからです (これらに何をかけても [1]6 にはならない!) また,[2]6,[3]6,[4]6 の行には,[2]6 × [3]6 = [0]6 という ”かけ算” としてはオカシナこともおきています。 一般に,
ある b≠0 に対して, a × b = 0
となるとき,a を零因子といいます。この用語を用いると,[0]6以外にもZ6には零因子が存在します。どのような元が零因子になっているかといえば,n が 1と n 以外の約数をもてば,a≠1 (そのとき,[b]n≠[0]n=[n]n ),かつ a× b = n となる a,b が存在して,
[a]n × [b]n = [a× b]n = [n]n = [0]n (0≦a,b<nとして考えてます。)
となることから,
| a が n の 1 以外の約数 ⇔ [a]n は零因子となる。 |
ことがわかります。
[4] また,[b]n≠[0]n の零因子 [a]n に逆元 [a]n-1 が存在すると,
[b]n = [a]n-1×[a]n × [b]n = [a]n-1×[0]n = [0]n
となり,[b]n≠[0]n に矛盾します。すなわち,
| 零因子は逆元をもたない。 |
そこで,Z6*の中で逆元をもつ元(←可逆元といいます)だけを抜き出した集合
G6 = {[1]6,[5]6}
× [1]5 [5]5 [1]5 [1]5 [5]5 [5]5 [5]5 [1]5
を考えるとこれは群をなすことがわかります。これは,「 Z6* から零因子を除外して群 G6を 得る。 」 ということができます。
[5] 以上,考察のもと次の定理が成り立ちます。
| 定理
Zn* の乗法における可逆元全体を (1) Gnは乗法群をなす。特に n が素数 p ならば,Zp* の元全体は乗法群をなす。 (2) [a]n ∈ Gn ⇔ a と n は互いに素 (3)|Gn|=φ(n) ただし,φ(n)はオイラー(Euler)のPhi 関数で となる。 |
また,Gn に属する剰余類を nと素な剰余類 ,Gnを既約剰余類群といいます。
注意: Zn*をはじめから可逆元全体の集合として定義することもあります。その時は,Zn*≡Gn です。実際,第2部では,Zn*≡Gnとします。
[6] また,Zn*は加群 Zn の自己同型群(自分自身へ写す全単射からなる群)Aut (Zn) ともなっています。
|
定理 巡回加群 Znについて, Aut (Zn) ≡ Zn* (mod n) である。(Zn*≡Gn) |
証明 略
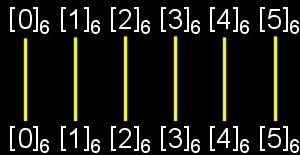
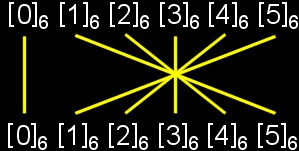
例 Z6の場合
この自己同型写像は,6の剰余類を6の剰余類へ写す上への1対1写像で,生成元は生成元に写されることを考えると,次の2つであることが分かります。
| ε | α | |
 |
 |
|
| Z6の自己同型写像はこの2つ | ||
これらε,αが自己同型写像であることは,εは自明ですが,αについては,
α([a]6)+α([b]6)=[6-a]6+[6-b]6=[6-(a+b)]6=α([a+b]6
と確認できます。この自己同型群Aut (Zn)は,次の群表から分かるように,Zn*(≡Gn) と同型です。
| Aut (Zn) | Zn* | |||||||||||||||||||
|
≡ 同型 |
|
||||||||||||||||||
補遺
・具体的なオイラーのΦ関数の形:
n=p1a・p2b・・・・pkrとするとき,(piは互いに異なる素数)
φ(n)=n 1− 1 1− 1 ・・・・ 1− 1 p1 p2 pk
=p1a-1p2b-1・・・・・pkr-1(p1−1)(p2−1)・・・・(pk−1)
最初のいくつかを計算してもみましょう。
n= 1 2 3 4 5 6 7 8 ・・・ φ(n)= 1 1 2 2 4 2 6 4 ・・・ 素な数 1 1 1,2 1,3 1,2,3,4 1,5 1,2,3,4,5,6 1,3,5,7 ・・・
例: n=p1a・p2b (k=2) のときについて考えると,
φ(n)は,nからp1で割り切れる数の個数とp2で割り切れる個数を差し引いて,そこへp1とp2の両方で割り切れる数の個数を加えればよい。すなわち,
φ(n)=n−n/p1−n/p2+n/(p1・p2)
=p1ap2b−p1a-1p2b−p1ap2b-1+p1a-1p2b-1
=p1a-1p2b-1(p1−1)(p2−1)
となって関係式を確認できる。 (問題:kが一般の正整数のときについて証明せよ。)
1からp1aまでの数の中で,p1で割り切れる数の個数は,p1a/p1 なので,これを引いた,
p1a−p1a/p1=p1a-1(p1−1)
が1からp1aまでの数の中で,p1で割り切れない数の個数である。
また,1からp2bまでのなかでの中でp2で割り切れない数の個数は,同様に考えて,
p2b-1(p2−1)
である。したがって,1からn=p1a・p2b のなかで,p1とp2のどちらでも割り切れない数の個数は,
p1a-1(p1−1)p2b-1(p2−1)
・n と素な整数 a に対して,
aφ(n) = 1 (mod n)
オイラーの関係式
pm を小さい方から数えて m 番目の素数とすれば,
1 ns = 1
1− 1 pms
が成り立ちます。 この関係式を示すのには,次の公式を用います。
1 = 1+r+r2+・・・+rn+・・・・ , ただし,|r|<1 1− r
| r として, | 1 | < 1 代入すれば, |
| pms |
1 = 1 +
1 pms +
1 pm2s +
1 + ・・・・・ pm3s
1− 1 pms
したがって,
1 = 1 +
1 2s +
1 22s +
1 + ・・・・・ 23s
1− 1 pms
× 1 +
1 3s +
1 32s +
1 + ・・・・・ 33s ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
× 1 +
1 5s +
1 52s +
1 + ・・・・・ 53s
これを展開すれば,
= Σ 1 α,β・・・ (p1αp2βp3γ・・・・・)s
ここで,Σは(α,β,・・・)は,0 以上のあらゆる整数の組についてわたってとります。すると,自然数が一意的に
p1αp2βp3γ・・・・・pkω (α=β=・・・=0 のとき,1 です。)
のように表せることから,この級数の( )sの中にはすべての自然数が1回ずつ現れます。よって,この和は,
1 ns
と書いてよいことがわかります。