Appendix　b2  ２面体群
f-denshi.com  更新日：　順次追加していきます
［目次へ］

１．n次の２面体群D_nの定義

［１］   次のような 2n 個の2次の正方行列の集合：

｛ 1，c，c2，   ･･･， cn-1， 　　σ，cσ，c2σ，･･･，cn-1σ　｝

c ＝ cos 2π n −sin 2π n sin 2π n cos 2π n σ ＝ -1 0 0 1 （ n ＝ 0，1，・・・，n-1 )

は行列の積に関して演算のもとで群をなします。この群を n 次の２面体群，D_n ＝＜c，σ＞ と言います。

　　これは 正n面体 の中心 O の周りの 2π/n　の回転 c と x 軸の周りの裏返し操作 σ を生成元とする幾何学的な意味を付与できる群と考えることもできます（下図）。

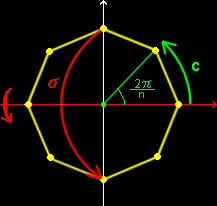
ここで，c，σ は次のような関係を満たしており，生成元は，c とσであることもわかります。　

cⁿ＝1，　σ²＝1， c^-1 ＝ σcσ  

正規部分群は，Z_n＝｛1，c，c²，   ･･･， c^n-1｝

［２］ 特に２次の2面体群 D₂ をクラインの４元群と呼び，群表 (乗積表) は次のようになります。

* 1 c σ cσ 1 1 c σ cσ c c 1 cσ σ σ σ cσ 1 c cσ cσ σ c 1

D2

行列で表現すると，

１　＝			1	0		， ｃ　＝			-1	0
			0	1					0	-1

σ ＝		1	0		，cσ＝			-1	0
		0	-1					0	1

これは３次正方行列でも表せます。　

［３］ ３次の２面体群 D₃ ＝S₃　である。

元の対応は次のとおりです。

1 ⇔ e =  1 2 3  1 2 3	c ⇔ a =  1 2 3  2 3 1	c2 ⇔ b =  1 2 3  3 1 2
σ ⇔ x =  1 2 3  1 3 2	cσ ⇔ y =  1 2 3  2 1 3	c2σ ⇔ z =  1 2 3  2 3 1

［４］　D_ｎ の中心は，

n＝		奇数：	Z（Dｎ ）＝ ｛ e ｝
		偶数：	Z（D2 ）＝D2　＝｛1,c,σ,cσ｝＝D2　（可換群） Z（Dn≠2 ）＝｛ e，cn/2 ｝

例

D₄＝｛ 1，c，c²， c³，σ，cσ，c²σ，c³σ　｝ならば，Z（D_ｎ ）＝｛ e，c² ｝

［５］　D_nの交換子群：

［Dｎ，Dｎ］＝		奇数（n＝2m＋1）：	Z2m＋1＝｛ e，a，a2，a3，･･･，a2m  ｝
		偶数（n＝2m）　　：	Zm    ＝｛ e，a2，a4，･･･，a2(m-1) ｝

２．D_nの分解

［１］

D₂ ＝ Z₂ × Z₂ であることは直積のところで述べています。 ⇒ [#]

* (+1,+1) (-1,+1) (+1,-1) (-1,-1) (+1,+1) (+1,+1) (-1,+1) (+1,-1) (-1,-1) (-1,+1) (-1,+1) (+1,+1) (-1,-1) (+1,-1) (+1,-1) (+1,-1) (-1,-1) (+1,+1) (-1,+1) (-1,-1) (-1,-1) (+1,-1) (-1,+1) (+1,+1)

Z2 × Z2

［２］　例

D₆ ＝｛ 1，c，c²， c³，c⁴， c⁵，σ，cσ，c²σ，c³σ，c²σ，c³σ｝
　　＝S₃×Z₂ ＝（α，β）　
ただし，
　　　　α＝e，a，b，x，y，z，　∈S₃　[#]
　　　　β＝1，-1　　　　　　　　∈Z₂

D₆とS₃×Z₂の対応は，

［５］ 分裂する完全系列の例：

直積で表される場合，分裂する完全系列となる，次のように表現する。

例

			i		f
1	→	S3	→	D6	→	Z2	→	1

［７］　

準同型写像：

ｆ ： Dn⇒Z2		f（ck）   ＝ 1
		f（ckσ）＝-1

核は：　Z_n＝｛1，c，c²，･･･，c^n-1｝；　　　D_n/Z_n ＝ Z₂

［８］

D_n は正規部分群 Z_n と部分群 Z₂ の半直積である [#]　⇔　　D_n＝Z_n Z₂　かつ， Z_n ∩ Z₂＝ 1

D₂は直交群 O（2） の部分群である。

［９］

[ 10]

［目次へ］