| Appendix b3 線形群・運動群 | ||
| f-denshi.com 更新日: しばらく項目だけ挙げておきます。21/09/24 | ||
| [目次へ] | ||
[1] 逆行列をもつ正則な ( |A| ≠0 である ) n次正方行列全体の集合は通常の行列の掛け算において群をなします。これを
一般線形群 GL(n,K)
といいます。ここで,K は任意の体ですが,ここでは実数 R,または複素数 C と考えます。
この群はさらに次のように分類されます。
− 正則行列 * A-1 = tA ( = A*) 一般
detA≠0GL(n,R)
実一般線形群⊃ O(n)
直交群 detA=±1GL(n,C)
複素一般線形群U(n)
ユニタリ群 |detA|= 1- ∪ ・ ∪ 特殊
detA=1SL(n,R)
実特殊線形群⊃ SO(n)
特殊直交群(回転群)SL(n,C)
複素特殊線形群SU(n)
特殊ユニタリ群
群どおしの関係
二重線:正規部分群と核(緑)
表の説明をしておくと,各行列の定義は以下のとおりです。(A*:転置複素共役)
GL(n,K)={ A | detA≠0 } O(n) ={ A | A-1 = tA , detA=±1 } U(n) ={ A | A-1=A* ,| det A | = 1 } SL(n,K)={ A | detA =1 } SO(n)={ A | A-1 = tA , detA = 1 } SU(n)={ A | A-1=A* , detA = 1 }
各行列の名前について補足しておくと,
一般 = 裏返しを含む
⇔
特殊 = 裏返しを含まない detA=1
[2] 2次正則行列の特別な形については
a b ,ad-bc ≠0 c d ∈ GL(n,RまたはC)
a b ,ad-bc =1 c d ∈ SL(n,RまたはC)
a b ,ad-bc =±1 c d ∈ O(2)
a b ,| ad-bc | =1 c d ∈ U(2)
cosθ -sinθ ,cos2θ+sin2θ=1 sinθ cosθ ∈ SO(2)
α -β* , |α|2+|β|2=1 β α* ∈ SU(2)
α=a+bi, β=c+di
⇒ |α|2+|β|2=1 ⇔ a2+b2+c2+d2=1
解説
O(2) について,A tA=E (2次単位行列) を満たすことから,
A1= cosθ -sinθ または,A2= ーcosθ sinθ sinθ cosθ sinθ cosθ
のいずれかで表せることが分かります(θ:実数)が,
A1= SO(2)
A2= -1 0 cosθ -sinθ 0 1 sinθ cosθ
という関係にあります。したがって,
O(2)= 1 0 SO(2) ∪ -1 0 SO(2) 0 1 0 1
と O(2) は類別できることが分かります。ここで,
準同型写像 Φ: A∈O(2) → detA ∈S0
核: SO(2)
代表系: 1 0 , -1 0 0 1 0 1
とすれば,
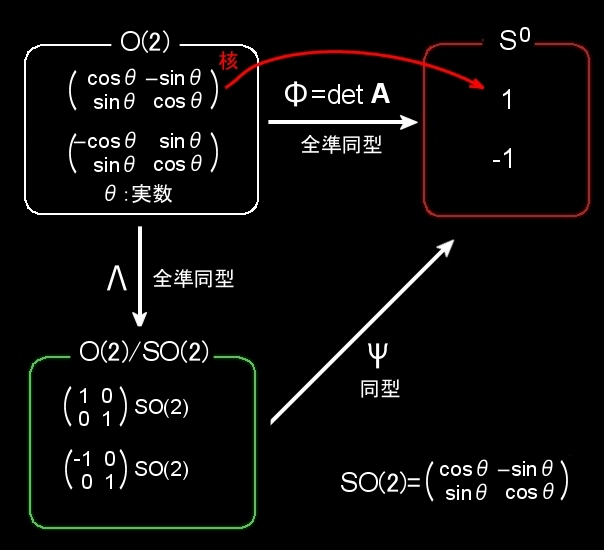
のような準同型定理を確かめることができます。
・ U=eiH∈U(2) と表すと, eiH=eiH* ⇔ H=iH* (エルミート行列)
[3] 特殊基本行列を,j,k=1,2,・・・,n; j≠k として,
| P = | 1 | 0 | ・・ | ・・ | 0 | ・・ | 0 | ,および,Q = | 1 | 0 | ・・ | ・・ | ・・ | ・・ | 0 | |||||
| 0 | ・・ | 0 | : | : | 0 | ・・ | 0 | : | ||||||||||||
| 0 | ・・ | 1 | 0 | λ | ・・ | 0 | ←j 行目 | : | 0 | 1 | 0 | : | ||||||||
| : | ・・ | ・・ | 0 | : | : | 0 | μ | 0 | : | |||||||||||
| : | 1 | : | : | 0 | 1 | 0 | : | |||||||||||||
| : | : | ・・ | 0 | : | 0 | ・・ | 0 | |||||||||||||
| 0 | ・・ | ・・ | ・・ | 0 | 0 | 1 | 0 | ・・ | ・・ | ・・ | ・・ | 0 | 1 | |||||||
| ↑ | ||||||||||||||||||||
| k 列目 | μ≠0 | |||||||||||||||||||
とすれば,
GL(n,K)の生成元は,P と Q である。
SL(n,K)の生成元は,P である。
[4] 中心Z は,
GL(n,K) ただし, E : n次の単位行列, K* = K−{ 0 }
SL(n,K) K=R のとき, K=C のとき,
Z(SL(n,R)) n=奇数: = { E } n=偶数: ={ E ,−E } Z(SL(n,C))={ cE|c∈C,かつ,cn=1}具体的には,
c ={exp(2πmi/n)},m=0,1,・・・,n-1
[5] 交換子群
[GL(n,K),GL(n,K)]=SL(n,K)
[SL(n,K),SL(n,K)]=SL(n,K)
GL(n,K)/[GL(n,K),GL(n,K)]=K* ← 可換群
[6] 準同型写像を考える
(1) GL(n,K)⇒K*への準同形写像 Φ(A)=detA の核は,SL(n,K)。
(2) O(n)⇒S0 への準同形写像 Φ(A)=detA の核は,SO(n)。
(3) U(n)⇒S1 への準同形写像 Φ(A)=detA の核は,SU(n)。
ただし,
K*=K−{0}
R*=R−{0}
R+={x∈R|x>0}
C*=C−{0}
S0={x∈R | |x|=1}={1,-1}
S1={c∈C | |c|=1}={eiθ}
したがって,
GL(n,K) の正規部分群は SL(n,K)
O(n) の正規部分群は SO(n)
U(n) の正規部分群は SU(n)
[7] 準同型定理を適用
| 準同型写像 Φ | 核 KerΦ | 準同形定理 | |
| 乗法群 R* ⇒ R+ | Φ(x)=|x| | S0 | R*/ S0= R+ |
| 乗法群 C* ⇒ R+ | Φ(c)=|c| | S1 | C*/ S1= R+ |
| 加群 R ⇒ S1 | Φ(x)=exp(2πxi) | Z | R/Z=S1 |
| GL(n,K) ⇒ K* | Φ(A)=detA | SL(n,K) | GL(n,K)/SL(n,K)=K* |
| O(n) ⇒ S0 | Φ(A)=detA | SO(n) | O(n)/SO(n)=S0 |
| U(n) ⇒ S1 | Φ(A)=detA | SU(n) | U(n)/SU(n)=S1 |
上の例を一般化すれば,次の定理が容易に導かれます。
|
定理 直積群 G1×G2 の正規部分群 G1’={(x1,1)|x1∈G1}による剰余群 (G1×G2)/G1’は G2 に同型である。 |
・ 2次回転群 SO(2)は群 S1={c∈C||c|=1}と準同型
| 準同型写像 Φ | 核 KerΦ | 準同形定理 | |
| SO(n+1) ⇒ Sn SO(3) ⇒ S2 |
SO(n) SO(2) |
SO(n+1)/SO(n)=Sn SO(3)/SO(2)=S2 |
|
| O(n+1) ⇒ Sn O(3) ⇒ S2 |
O(n) O(2) |
O(n+1)/O(n)=Sn O(3)/O(2)=S2 |
|
R(θ)∈SO(2)≡S1≡U(1)
SU(2)≡S3
SO(3)≡RP3
2.アフィン変換群
[1] アフィン変換群・合同変換群の定義
|
定義 n次元ユークリッド空間における次の写像φ全体, (1) A(Rn)={ φ: Rn→Rn|φ(x)=Ax+b ,A∈GL(n,R),b∈Rn } (2) E(Rn)={ φ: Rn→Rn|φ(x)=Ax+b ,A∈O(n),b∈Rn } をそれぞれ,(1)アフィン変換群,(2)合同変換群(=運動群)という。 |
これらが合成写像を算法として群を作ることは容易に証明できる。
(1),(2)の場合
単位元: e(x)=Ex+0
逆元 : φ-1=A-1x−A-1b
[2] ユークリッド空間内の一点をユークリッド空間の1点に写す次の3つの写像,
(a) 平行移動
(b) 回転
(c) 反転
を有限個合成して得られる写像全体の集合は群をなします。これは行列を用いて,
E(Rn)={φ|φ(x)=Ax+b, A∈O(n),x,b ∈Rn }
と表すことができ,合同変換群と言います。特に,平行移動を表す群は,
(3) D(Rn)={ φ: Rn→Rn|φ(x)=x+b }
という記号で書くこととします。
[3] これら群の主な包含関係
A(Rn) ⊃ E(n) ⊃ E+(n) ⊃O(n),Rn
O(2) ⊃ Dn
C* ⊃ S1 ⊃ Zn
[4] 準同型定理
| 準同型写像 Φ | 核 KerΦ | 準同形定理 | |
| A(Rn) ⇒ GL(n,R) | Φ(Ax+b)=A | D(Rn) | A(Rn)/D(Rn)=GL(n) |
| E(Rn) ⇒ O(n) | Φ(Ax+b)=A | D(Rn) |
E(Rn)/D(Rn)=O(n) |
完全系列
α β 1 → SL(n,R) → GL(n,R) → R* → 1
α β 1 → SO(n) → O(n) → S0 → 1
α β 1 → SU(n) → U(n) → S1 → 1
ここで,
直和分解
GL(n,R)=R+×SL(n,R)×R+
であることに注意すれば,
例
H(3)
0 En -En 0 SP(n)
S3 ⇒ RP3 ||| Uと-Uを同一視 ||| U ∈SU(2) 等長対応 U~ ∈SO(3)
X= x z* z x ∈SO(2)
Y= y w* w y ⇔
⇔
対応x=(x,z),
y=(y,w)
∈R×C=R3detX=x2-zz*=1 U*XU
(U*XU)*=U*XU
(-U)*X(-U)=U*XU作用 U~x
1 tr(XY) 2 内積
xy+Re(z*w)<x,y> <U*XU,U*YU>
= 1 tr(XY) 2 <U*~x,U~y>
=<x,y>
対称群 Sn からZ2{1,-1}への写像: f(σ)=sgnσ
| 位数 | 群 |
| 2 | Z2 |
| 3 | Z3 |
| 4 | Z4, Z2×Z2=D2 (クラインの4元群) |
| 5 | Z5 |
| 6 | Z6, S3=D3 |
| 7 | Z7 |
| 8 | Z8, Z4×Z2, Z2×Z2×Z2, D4, Q (4元数群) |
| 9 | Z9, Z3×Z3 |
| 10 | Z10,D5 |
| 11 | Z11 |
| 12 | Z12,Z6×Z2,S3×Z2=D6,A4 |
| 13 | Z13 |
| 14 | Z14, D7 |
| 15 | Z15 |
| 被覆空間 M 普遍被覆 → |
商空間 M/G 軌道空間 |
被覆写像 | 作用する群G (リー群) |
作用方法 |
| s∈R → | S1 | π1 (s)=exp(is) | n∈Z | s→s+nπ |
| (s,t)∈R2 → | S1×R | π2 (s,t)=(exp(is),t) | n∈Z | s→s+nπ |
| (s,t)∈R2 → | T2 | π3 (s,t)=(exp(is),exp(it)) | n∈Z,m∈Z | s→s+nπ,t→t+mπ |
| S2 → | S2 | |||
| 開円板D | 種数2以上の 閉曲面 |
| 群 | 位相多様体としての次元 |
| GL(n,R) | n2 |
| GL(n,C) | 2n2 |
| GL(n,H) | 4n2 |
| O(n) | n(n-1)/2 |
| U(n) | n2 |
| Sp(n) | n(2n+1) |
| SO(n) | n(n-1)/2 |
| SU(n) | n2-1 |
| G2 | 14 |
| F4 | 52 |
| E6 | 78 |
| E7 | 133 |
| E8 | 248 |