 |
プランクの放射公式と3つの比熱理論の比較 |
| f-denshi.com 更新日: 21/08/25 |
| サイト検索 |
| 目次へ |
1.プランクの輻射公式 (放射公式)
20 世紀の量子力学の発見につながる19世紀末の物理問題として,熱輻射エネルギーの温度・波長依存性の理論式の決定がありました。一般的な白熱球は,フィラメントに電流を流して2800
℃ほどに発熱させることで投入電力の10 %に相当する可視光と70 %ほどの赤外線を発しています。白熱球に限らず,物体は熱せられると光を放ちますが,温度が高くなるにつれて,より短波長へシフトしていきます。これを利用して高温物体の温度を測定できないか,特に高炉内の温度を正確に測定・制御することは当時,重要な課題でした。
最終的にはプランクがプランクの輻射公式 (プランクの放射公式)を導くことに成功し,量子力学の発見へとつながっていくのですが,この辺の歴史的な経緯に沿った説明は統計力学や量子力学の教科書のみならず,多くの啓蒙書もありますので,そちらを参考にして下さい。(もちろん,ネット上にもたくさんあります。)
現代の統計力学的知見をもつ読者に対しては,電磁波が調和振動子の集まりとして記述できるということさえ受け入れれば,プランクの輻射公式は固体比熱のデバイモデル
[#] から以下の変更を行うだけで得られることに気が付くことでしょう。
電磁波は横波として2 つの自由度を持つので,電磁波の振動数の状態密度は,デバイモデルから,
| g(ν)=4πV |
 |
1 |
+ |
2 |
 |
ν2 [デバイ] ⇒ g(ν) = 4πV |
 |
2 |
 |
ν2 [熱輻射] ・・・ (1) |
|
|
|
| cl3 |
ct3 |
c3 |
と変更されます。ここで,c は光速度です。
もう一つの変更点は,考慮する振動数の上限を設けないことであり,
νD (デバイ振動数) [デバイ] ⇒ ∞ [熱輻射]
と変更します。
つまり,振動数ν とν + dν にある電磁場(輻射場) のエネルギーは,デバイモデルの
(4) 式 ,
E(ν)dν=
|
|
hν |
|
| exp |
 |
hν |
 |
− 1 |
|
| kT |
|
|
・g(ν)dν [デバイ固体熱エネルギー] ・・・ (4)
|
における g(ν) を熱輻射に対する状態密度 (1)式に置き換えて,
E(ν)dν=
|
|
hν |
|
| exp |
 |
hν |
 |
− 1 |
|
| kT |
|
|
 |
|
 |
ν2 dν [プランクの輻射公式×V] ・・・ [*] |
|
|
|
と表して,これを V で割り,体積エネルギー密度 u に変えて,振動数νで0から∞まで積分すれば,
| u= |
|
= |
|
 |
|
hν3 |
|
| exp |
 |
hν |
 |
− 1 |
|
|
| kT |
|
|
dν
|
となり,輻射場のエネルギー密度が T の4 乗に比例するというシュテファン-ボルツマンの法則が得られます。途中で,デバイの比熱を計算したとき [#] と同様に,
と置き換えています。また,被積分関数は”デバイ関数”と同じですが,ここでは積分範囲が∞
のため (π4/15) と計算できます。
(注意) 輻射のエネルギー密度 u と輻射の輝度L との関係,L=(c/4)u を用いて,
の形でシュテファン-ボルツマンの法則を示している文献も多い。σはシュテファン-ボルツマン定数と呼ばれる。
輻射場の比熱は [**] 式を温度で微分すればよく,
「輻射場の比熱は温度 T の3 乗に比例する。」
ことも分かります。これは固体比熱の場合とは違い,低温だけでなく,任意の温度で成り立ちます。
プランクの輻射公式を波長 (λ = c/ν) で表しておくと,
| − |
|
 |
|
1 |
|
| exp |
 |
hc |
 |
− 1 |
|
|
| λkT |
|
|
dλ 波長表示 ・・・・ [**]’ |
次にいくつか近似式を示しますが,プランクの輻射公式の長波長領域 (低振動数領域) では,[*]の指数部分を1次式で近似して,体積密度表示で,
となりますが,これはレーリー-ジーンズの放射式と呼ばれています。
一方,短波長領域 (高振動数領域) では,exp(hν/kT) >> 1 と近似して,
| u(ν)= |
|
exp |
 |
− |
|
 |
振動数表示 |
| u(λ)= |
|
exp |
 |
− |
|
 |
波長表示 |
これはウィーンの輻射式 (1896年) と呼ばれます。この式はスペクトルにピークを与え,実験事実を定性的に説明します。輝度を示したいときは
c/4 を乗じます。
同じく,ウィーンの名を冠した,ウィーンの変位則というのもあります。これは温度 T の物体から得られる輻射のスペクトルの
「ピーク波長λmax と温度 T との積は定数」
であることを主張します。温度 T の物体の輻射のスペクトルのピーク波長は[**]’ をλ で微分して,= 0 とすれば,
| 5 (e-x−1) = x ただし,x =hc/λmaxkT |
が得られます。この左辺はx の指数関数で,右辺はx の1 次関数なので,これはx
が定数でなければ満たされません。(実際,両辺の関数は x>0 で1点で交わる) つまり,
λmaxT = 定数
でなければいけません。
3種類の比熱の理論:アインシュタインモデル(1910年),デバイモデル(1912年),プランクモデル
(1900年) については,歴史的な経緯は複雑ですが,この3 つモデルの統計力学的な関係は極めてシンプルです。
下図 に示すように,モデルに応じて調和振動子に適切な異なる状態密度の重みを付けてエネルギーを計算すればよいのです。比熱はそれらを温度で微分すれば求まります。
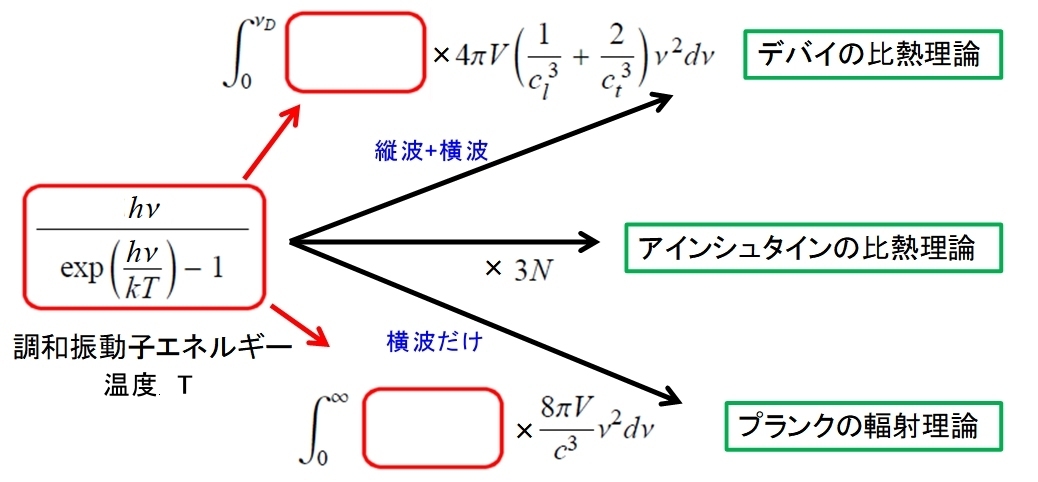 |
| 熱エネルギー算出方法を3つの比熱モデルで比較する。 |
[目次へ]
SUSTAINABLE TOKIWADAIGAK SINCE 2002
