t105　グランドカノニカル分布の導出
f-denshi.com  更新日：13/07/16　（仮）
サイト検索
目次へ

カノニカルアンサンブルの取り扱いでは系と外界との間での粒子交換を考えていませんでした。ここでは，外界とエネルギーだけでなく粒子の交換も行なうグランドカノニカル分布を導出します。　その導出方法はカノニカルアンサンブルの扱いとだいたい同じで，大きな孤立系の小さな一部分に着目することがポイントです。

１．グランドカノニカル分布（大正準分布）の導出

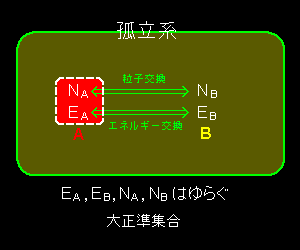
［１］　平衡状態にある孤立系（＝全系）を２つの系Ａと系Bに分けて考えます。このとき，系Ａは系Bに比べて非常に小さく，大きな系Bは，エネルギーと粒子を系Ａと交換できる熱粒子浴とみなせることとします。全系の微視的状態，および，全エネルギー，全粒子数は系Aと系Bの和であらわすことができ，下表のとおりとします。

− 全系 (A+B) 系Ａ 系B エネルギー E全　（一定） EA (変動) EB (変動) 粒子数 N全　（一定） NA (変動) NB (変動) 状態数 W全（E,V,N） WA（EA,VA,NA） WB(EB,VB,NB) W全(EA∩EB，NA∩NB) E全＝EA＋EB　　　　 ⇒　　　　0＝δE全＝δEA＋δEB N全＝NA＋NB　　　　⇒　　　　0＝δN全＝δNA＋δNB かつ，EA <<  EB  および，NA <<  NB

系Ａと系Ｂの境界には仮想的な境界が存在していると考えてもよいでしょう。化学反応に適用する場合などはこのような描像が当てはまらないのですが，それは頭の片隅に置いておくこととします。

平衡条件　（急ぐ場合は直感的に当たり前なのでここは，とばして見なくてよい。） カノニカルアンアンブルの場合と同じように考えて，平衡状態においては，最大確率分布が達成されている と考え次のような条件を得ます。 まず，考えている変数以外の固定する変数は省略して書くと，ボルツマンの原理より k log ［W全(EA∩EB)］＝k log ［WA(EA)WB(EB)］ 　　　　　　　　　　＝SA(EA)＋SB(EB)　　　(　＝　SA(EA)＋SB(E全−EA)　) ですが，平衡状態，EA*，EB*において，系が最大確率分布をとるとすれば，上式の最大値をとる条件として， ∂(SA(EA)＋SB(EB)) ＝0 ∂EA EA=EA*，EB=EB* すなわち，dEA＝−dEBに注意して， ∂SA(EA) ＝ ∂SB(EB) ⇔ 1 ＝ 1 ∂EA EA=EA* ∂EB EB=EB* TA* TB* が得られます。　ここで，熱力学公式， ∂S(E) ＝ 1 ∂U N,V T を援用しています。そこで，平衡状態における温度は，TA*＝TB*＝T　としましょう。 さらに，最大確率分布においては，粒子数の変化に対しても極値をとるはずです。すなわち， ∂(SA(EA)＋SB(EB)) ＝0 ∂NA NA=NA*，NB=NB* 今度は熱力学におけるエントロピーと化学ポテンシャルμ との関係[#]， ∂S ＝− μ ∂N E,V T を思い出すと，dNA＝−dNBに注意して，平衡条件を， ∂SA(EA) ＝ ∂SB(EB) ⇔ μA* ＝ μB* ∂NA NA=NA* ∂NB NB=NB* T T とすることができます。すなわち，系Ａ と B との化学ポテンシャルとは等しいということです。 μA*＝μB*　（＝μ） 結局，系Aと系Bが熱平衡にあるとき，それらの温度，および，化学ポテンシャルは等しくなければなりません。

グランドカノニカル分布の導出

［２］　全系 (孤立系) の状態の中で，系Ａ (考察対象) がエネルギーE_A，粒子数N_Aを持っており，残りの系B (熱粒子浴) がそれぞれE_B，N_Bを持つような状態数，W_全(E_A∩E_B，N_A∩N_B)は系Ａの微視的状態数W_A(E_A，N_A)と系Bの微視的状態数W_B(E_B，N_B)との積，

W_全(E_A∩E_B，N_A∩N_B)＝W_A( E_A，N_A)×W_B(E_B，N_B)
　　　　　　　　　　　　　　＝W_A( E_A，N_A)　×　W_B(E_全−E_A，N_全−N_A)　　　　　(3)

で表されます。すると，全系の状態数W_全(E_全)は上式の中で， E_A＋E_B＝E_全 (一定)，N_A＋N_B＝N_全 (一定)を満たすものをすべて拾い出して，和をとればよいので，

W全(E全)＝	Σ		Σ	W全(EA∩EB，NA∩NB)
	EA＋EB＝E全		NA＋NB＝N全

＝		Σ	Σ	WA( EA，NA)×WB(E全−EA，N全−NA)　　　　　(4)
		EA	NA

で表されることになります。また，等重率の原理から全系のこれら微視的状態の一つひとつの出現確率はすべて等しく，1/W_全(E_全)であると考えることができる，とするのはミクロカノニカルアンサンブルのときと同じです。

特に，系Ａの微視的状態の一つ rだけに着目し，その微視的状態のエネルギーをE_r（=E_A），粒子数をN_r（=N_A）と書くと，等確率で出現する全系の微視的状態の中で，系Ａの部分が微視的状態 r にある個数は，

W全(Er∩(E全−Er)，Nr∩(N全−Nr))＝　１　×　WB(E全−Er，N全−Nr)　　　(＝WB(EB，NB)　)

であることがわかります。すなわち，系Ａが微視的状態 r であるような全系の状態数は，熱粒子浴である系BがエネルギーE_B＝E_全−E_r，かつ粒子数がN_B＝N_全−N_rである状態数に等しいといえます。したがって，系Ａが微視的状態 r である確率は，

Pr＝	W全(Er∩(E全−Er)，Nr∩(N全−Nr))	←等重率の原理から
	W全(E全，N全)

＝	WB(E全−Er，N全−Nr)	∝　WB(E全−Er，N全−Nr)　　(＝WB(EB，NB)　)　　　　(6)
	W全(E全，N全)

となり，そのときの熱粒子浴の微視的状態数に比例することがわかります。

［３］　次に，ボルツマンの原理 S(E)＝klogW(E) を用いると，熱粒子浴の状態数は

WB(EB，NB)＝WB(E全−Er，N全−Nr) ＝ exp		SB(E全−Er，N全−Nr)		･････[*]
		k

とエントロピーと関係付けられます。さらに，E_全>>E_r (＝E_A) ，および，N_全>>N_r (＝N_A） に注意して，指数の肩の分子，S(E_全−E_r，N_全−N_r)をテーラー展開すると，

SB(E全−Er，N全−Nr) ≒ SB(EB=E全，NB=N全）＋		∂SB(EB，NB)		EB＝E全，NB=N全	(−Er)＋		∂SB(EB，NB)		EB＝E全，NB=N全	(−Nr)
		∂EB					∂NB

＝ SB(E全，N全)−	Er	＋	μB(E全，N全) Nr	(7)
	TB(E全，N全)		TB(E全，N全)

最後の変形では，熱力学公式，

∂S

＝

1

および，

∂S

＝−

μ

∂U

V,N

T

∂N

E,V

T

を用いました。さらに，熱粒子浴の温度T_B(E_全，N_全)を全系の温度T，μ_B(E_全，N_全)を全系の化学ポテンシャルμに等しいとできます。よって，(7)を[*]に代入して，

Pr∝ 　WB(E全−Er，N全−Nr) ≒exp		SB(E全，N全)		･exp		−	Er	＋	μNr		(8)
		k					kT		kT

［４］　さらに，１つ目の指数項は状態ｒに依存しない定数なので，確率の規格化定数Ξに含めてしまえば，

Pr ＝ 1 exp Nrμ−Er Ξ kT

ここで，Ξは確率の規格定数，

Ξ ≡ exp Nrμ−Er kT

を計算することで得られます。以上が温度Tの熱粒子浴に接している系の微視的状態r (エネルギーE_r，粒子数N_r) が出現する確率となります。

２．大分配関数と熱力学関数

［１］　まず，熱力学関数，グランドポテンシャルJ の定義を復習しておきます。

J(T,V,μ)≡F−μn　　　　　定義　　　　（さらに，F＝U-TS　を代入してもよい）

この微分は，　dF ＝−SdT−PdV＋μdn を思い出して，(nは粒子のモル数です。)

ｄJ ＝ −SdT−PdV−ndμ

ただし，ここではｎは粒子数と考えて定義する（モル数ではない）。これらより，ただちに，

S＝−			∂J
			∂T		V,μ

P＝−			∂J
			∂V		T,μ

n＝−		∂J
		∂μ		T,V

なる関係が得られます。

さらに，J/Tの全微分を，J＝U-TS−μn　として計算すると，

d J ＝ 1 dU− U dT−dS＋ nμ dT− n dμ− μ dn T T T2 T2 T T

これに，

dU＝TdS−PdV＋μdn　

を代入すると，

d		J		＝	−U＋nμ	dT−	P	dV−	n	dμ
		T			T2		T		T

さらに両辺，dV＝dμ＝0　の下で，dTで除し，数学表現を整えれば，

U＝−T2		∂		J				＋nμ　　　　　････　[**]
		∂T		T			V,μ

なる関係も得られます。

［２］　さて，話を統計力学に戻すが，大分配関数の対数をとり，逆温度βの関数とみて微分してみると，

logΞ　＝log		exp		Nrμ−Er		＝log		expβ(Nrμ−Er)
				kT

∂log Ξ	＝	1	・	∂Ξ	＝	(Nrμ−Er)expβ(Nrμ−Er)
∂β		Ξ		∂β		Ξ

＝μ	Nrexpβ(Nrμ−Er)	−	Erexpβ(Nrμ−Er)
	Ξ		Ξ

＝μ		Nrpr −		Erpr

　　　　　　＝μ<N>−<E>

ここで，変数βを温度Tに戻して[#]，<E>が左辺にくるように移項すると，

<E>＝kT2	∂logΞ	＋μ<N>
	∂T

［３］　この結果を[**]　と比較して，U⇔<E>，n⇔<N>と解釈すれば，

J(T,V,μ)≡−kTlogΞ(T,V,μ)

と対応づけてよいことが分かります。これは統計力学におけるグランドポテンシャルの定義です。

したがって，J　が　T，V，μの関数でわかっていれば，熱力学に対応する物理量として，

エントロピー

<S> ＝−			∂J			＝kT			∂logΞ(T,V,μ)
			∂T		V,μ				∂T		V,μ

圧力

<P> ＝−			∂J			＝kT			∂logΞ(T,V,μ)
			∂V		T,μ				∂V		T,μ

平均粒子数

<N> ＝−		∂J			＝kT		∂	logΞ(T,V,μ)
		∂μ		T,V			∂μ			T,V

＝ξ		∂	logΞ(T,V,ξ)
		∂ξ			T,V

平均（内部）エネルギー

<E> ＝−T2

∂

(J/T)

＋μ<N>

＝kT2

∂

logΞ(T,V,μ)

＋μ<N>

∂T

∂T

V,μ

＝−		∂	logΞ(β,V,μ)			＋μ<N>
		∂β			V,μ

を定義することは自然です。他にも，

ヘルムホルツ自由エネルギー

<F>＝J(T,V,μ)＋μ<N>　　＝−kTlogΞ(T,V,μ)＋μ<N>　　←グランドポテンシャルの定義より
　　＝J(T,V,ξ)＋<N>kTlogξ＝−kTlogΞ(T,V,ξ)＋<N>kTlogξ　　←絶対活量を用いた表現

が定義できます。2行目は，F＝J＋μnにおいて，次の化学ポテンシャルと絶対活量との関係を用いてます。

絶対活量との関係

ξ=exp(μ/kT)　　［絶対活量］　⇔　μ＝kTlog ξ　［化学ポテンシャル］

［４］　最後にグランドカノニカルアンサンブルの方法における一般的な作業手順について，下図にまとめておきます。

大正準集団の方法

→		→	→	→↓←	←
S(T,V,N)		P(T,V,μ)＝− ∂J ＝− J ∂V T,μ V		U(T,V,N)＝F(T,V,N)＋TS(T,V,N)
↑μ消去		↑		↑μ消去
S(T,V,μ)＝− ∂J ∂T V,μ	←	Ξ(T,V,μ) J(T,V,μ)＝−kTlogΞ	→	E ＝−T2 ∂ (J/T) ＋μN(T,V,μ) ∂T V,μ	↑
		↓
		N(T,V,μ)＝− ∂J ∂μ T,V	→ μで解く	μ＝μ(T,V,N)	↑
		↓
		F(T,V,μ)＝J(T,V,μ)＋μN(T,V,μ)	→ μ消去	F(T,V,N)	→

注意：　　「 J＝−PV 」は，G＝μn が成り立つ純物質に対してだけ成り立つ関係式。

［目次］

SUSTAINABLE　TOKIWADAIGAK　SINCE　2002

公式

∂	＝	∂	＝−kT2	∂
∂β		∂(1/kT)		∂T

ミクロカノニカル−，カノニカル−，グランドカノニカルアンサンブルの比較

３つのアンサンブルのどの扱いからも最終的に同じ熱力学量が導出されますが，
どれも同じ，好みの問題と言うわけではありません。

その統計数学モデルに含まれている微視的情報の質・量は全く違います。

３つのアンサンブルをざっくり比較すると下図のようになります。

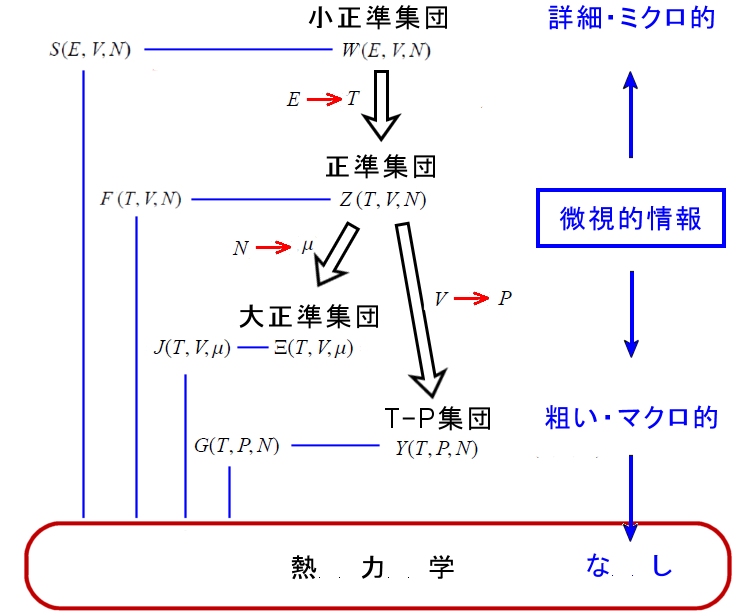
基本的には，ミクロカノニカルアンサンブルが最も詳細なモデルを与えるアンサンブルで，これが使えるならばベストです。　　⇒　イジングモデル

しかし，粒子間に相互作用があり，１粒子分配関数にそれを組み入れるのが難しいくなっていくと，カノニカル-やグランドカノニカルアンサンブルで取り扱う必要がでてきます。

すると，分子レベルの意味のしっかりしたパラメーターを含まないモデルとなり，巨視的なパラメーターが入ってきますが，そこに価値を持たせるのは使う人の才覚，努力次第と言うところかな？