| t110 古典理想気体1 | |
| f-denshi.com 更新日: 13/11/20 | |
| サイト検索 | |
| 目次へ | |
理想気体のミクロカノニカルアンサンブルとしての取り扱いを示します。
エネルギーEを指定する。
状態数をW(E,ΔE)を計算する。
エントロピーS(E)を求める(ボルツマンの原理)。
温度を定義する。
他の熱力学関数を計算する。
という順番に話を進めます。自由粒子の微視的状態数は量子力学の助けを借りて求めます。
注意: 状態数を求めるために量子力学を援用しますが,それだけで量子統計とは呼びません。
量子統計はあくまで,系の波動関数の(反)対称性を考慮にいれた,
フェルミ-ディラック統計とボース-アインシュタイン統計です。
このページはすべて修正古典統計によって扱われています。
[1] 箱の中におかれたエネルギーεをもつ1つの自由粒子を考えます。まず,3次元空間の自由粒子の量子状態は[#],
シュレーディンガー方程式
i h∂ ψ(x,t) =−
h2・ ∂2 ψ(x,t) ・・・・[0] ∂t 2m ∂x2
波動関数
ψ(r,t)=exp [−iεt/h]exp [ikr]
=exp [ikr−iωt]
=exp [i(kxx+kyy+kzz−ωt)] ・・・・・ (1)
ただし,ω=(hk2)/(2m)
・・・・・ (2)
エネルギー
ε(k ) =ε(k)= (h2k2)/(2m) (= p2/2m)
=h2(kx2+ky2+kz2)/(2m) ・・・・・ (3)
ここで,
k=|k|, k = (kx,ky,kz), dε=dk・kh2/m, r = (x,y,z)
を満足します。ここで使われている記号は量子力学 102 を参照(復習)してください。
[2] さらに,この粒子が実空間の1辺 L の立方体 (体積:V=L3) の中に存在しているとすれば,その量子力学的な取り扱いをまとめると次のようになります。
自由粒子に周期境界条件:
ψ(x+L,y,z,t)=ψ(x,y,z,t) を設定すると, kxL=2πnx : nx= 整数 を満足します。 すなわち,
nx,ny,nz = 0,±1,±2,・・・ |
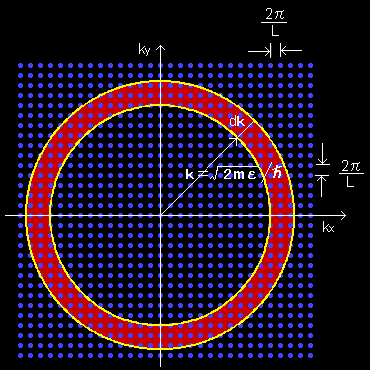 |
この結果は,( kx,ky,kz )で指定される粒子の状態は飛び飛びの値をとり,1辺が 2π/L の立方格子点(=1つの格子点のk空間での占有体積=(2π/L)3)で表すことができ, 3次元 k 空間を埋め尽くしています。 なお,上図では煩雑さを避けるために,この3次元空間の( kx,ky )平面での断面(2次元)で示しました。
ミクロカノニカルアンサンブルの方法では,与えられたεに対して(3)を満足する (kx,ky,kz),または, (nx,ny,nz)の組を数え上げれば,原理的に状態数W(E,V,N=1)が求まり,ボルツマンの原理からエントロピーをはじめとして他の熱力学量が導かれてくるわけですが,|k|が大きな値をとるときはこれを実行することは困難を伴います。
[3] そこで,状態数W(E,V,N=1)をEの連続関数とみなす,近似の適用を考えます。
その場合,3次元のk-空間の単位体積あたりの状態数(=状態密度)は,
1 = V , [状態密度] ただし,V = L3 (2π/L)3 (2π)3
とk-空間内を均一に分布しているとします。 また,このk-空間においてはエネルギー ε(k)=ε 一定の球面は(3)より,
|k| =
kx2+ky2+kz2 =
2mε =
2π 2mε [半径] hh
および,
|Δk| = k Δε 2ε
を満たす半径k の球面となります。 エネルギー 0 からεまでの状態数 W0(ε) は,この球の体積の1/8に状態密度を乗じて,
↓ (3)式より
W0(k) ≡ 4π k3 × V ×(1/8)・・・・・(4)3 (2π)3 球の体積 状態密度
W0(ε) = 4πV (2mε)3/2 3h3
と計算されます。(1/8)は球の第1象限だけある部分だけを数えるために乗じています。さらに,半径kとk+Δkと間にある球殻の状態数は,Δk<<kとして,
ΔW=W(ε,Δε) =W0(k+Δk) −W0(k)
≒ 4πk2Δk× V ×(1/8)(2π)3
= 4πk3V Δε 2ε(2π)3
= 2πV 2m 3/2
ε Δε h2
[4] また,k もεも連続変数とみなして,エネルギーεの関数としての状態密度Ω(ε)を,
Ω(ε) ≡ dW0(ε) =2πV 2m 3/2
ε (≡ D(ε) とも書く) [1粒子状態密度] dε h2
と定義すると,理想気体,1粒子のエネルギーε 〜 ε+Δε にある状態数は,
W(ε,Δε) = Ω(ε)Δε
= 2πV 2m 3/2
ε Δε ・・・・( ) h2
ここで,W(ε,Δε) がどの程度の数なのか見積もってみましょう。係数部分を 2m=10-25kg,h=6.6×10-34m2kg/s,2πV=1m3とすると,
W(ε,Δε) 〜1066
ε Δε
さらに,εとして,数100度の気体分子の運動エネルギーを考えて,10-20Jとすると,
W(ε,Δε) 〜1036 Δε ε
と表すことができます。最後にΔε/εは測定精度の桁数として7桁を想定すれば10-7。結局,1粒子の取り得る状態数としては,W(ε,Δε) =1029と見積もられます。これはアボガドロ数よりも相当大きな数です。
[5] 以上,出てきた重要な統計力学用語をまとめておきます。
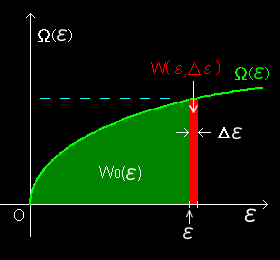 ここまでの用語のまとめ ここまでの用語のまとめ
ある1粒子エネルギー,0 〜 ε との間にある状態数をW0(ε)とすると,
ここで,状態密度:Ω(ε)は によって与えられる。 ε 〜 ε+Δε にある状態数, (ε−Δε〜εの範囲で考えても同じ。)
|
|||||||||||||||||||||||
: 離散確率変数と連続確率変数イカサマでなければ,サイコロを振り1の目が出る確率は6分の1となります。では,ふらりとバス停にゆき,正確に6分間隔で運行されているバスをちょうど1分待つ確率はいくらでしょうか?もちろん,6分の1ではありません。答えは0です。バスの待ち時間をいくらに設定しようと,1点で指定した待ち時間でバスがやってくる確率はすべて0です。
この違いは前者は離散的な確率変数で考えているのに対して,後者は連続的な確率変数で考えるているからです。サイコロの場合は,1から6までの6つの有限個の整数の中から無造作に1という一つの数が選ばれる確率を計算しています。それに対してバスの場合は時間が連続変数なので,0から6までの無限個ある実数の中から1という一つの「実数」が選び出される確率を計算しなければなりません。したがって,1÷∞=0という計算になってしまうのです。
しかし,これでは無意味なので,問題を設定し直して意味を持たせる必要があります。どのようにすれば良いのかといえば,待ち時間に幅を持たせるのです。例えば,「1分以上2分以下の待ち時間となる確率」であるならば,6分間の内の1分間でバスがやってくる確率となるので,6分の1と確率を計算することができます。
一般的には,連続確率変数Xで表される事象が起きる確率は,適当な確率密度関数 f(x) を用いて,
P(E≦X≦E+ΔE) = E+ΔE f(x)dx ≒f(x)ΔE E のような形式で定義されます。P(E≦X≦E+ΔE)とは,確率変数XがEとE+ΔEとの間の値をとる確率と言う意味です。また,f(x)の原始関数F(x)を考えると,それはXが0からxの間にある値をとる確率と考えることができます(積分定数を0として)。
以上の数学的な背景に基づけば,ΔEの値は必ずしも小さな値や微分量である必要はなく,状況に応じて自由に定めて良いことがわかります。
ただし,ΔEはいくらでも小さな値を想定してよいわけではなく,離散変数を連続変数と近似して,微分積分を行うわけですからΔEの幅の中にある状態数が「巨視的」である必要があります。
ここでは,そのような仮定は成り立つとしているのですが,ボース理想気体の低温では成り立たなくなることを後ほどみることとなります。
ミクロカノニカル集合ではどんなE,V,N に対しても状態密度は同じ
[1] 今度はN個の自由粒子の場合について考えてみましょう。その場合は3N次元のk-空間を考えることになるので,先ほどの(4)式,
W0(k) ≡ 4π k3 × V 3 8π3 球の体積 状態密度
において状態密度を,
V ⇒ V N 8π3 (2π)3
球の体積を,3N次元の球の体積
4π k3 ⇒ 2(2π)3N (2πmE)3N/2 3 3NΓ(3N/2)h3N
に変更しなければなりません。ただし,同時に1粒子に対応するエネルギーεから,N粒子系に対応する E へと記号を変更しておきましょう。すると,
W0(E,N) ⇒ 2(2π)3N (2πmE)3N/2× V N 3NΓ(3N/2)h3N (2π)3
= 2(2πm)3N/2・VN E3N/2 3NΓ(3N/2)h3N
= 2(2mπ)3N/2・VN E3N/2 3Nh3N・Γ(3N/2)
[2] さらに,同じ空間内を自由に動きまわる同一種類の気体分子を一つひとつ区別することは意味のないことであることから気体分子数 N!で割って,
W0(E,N) = 2(2mπ)3N/2・VN E3N/2 3Nh3N・Γ(3N/2)N!
とします。ここで,W0(E,N)は,N!で割る前と同じ記号を使い続けることとします。 したがって,N個の自由粒子の状態密度および,状態数は,
Ω(E,N) = dW0(E) = (2mπ)3N/2・VN E(3N/2)-1 = 3N W0(E,N) [状態密度] dE h3N・Γ(3N/2)N! 2E
W(E,N,ΔE ) =Ω(E,N )ΔE [状態数]
となります。
なお,N!で割ったからといって量子統計の効果を正確に取り込んだことなどにはならないことに注意せよ。
あくまで,場当たり的修正に過ぎない。 こちらをみよ ⇒ [#]
N粒子系状態密度関数の概形
とんでもない急激な増加関数である!
| 補足1: n次元球の体積VnのΓ関数を用いた表現
半径r のn次元の球の体積Vn はガンマ関数を用いて,
で与えられる⇒[#]。さらに,この球の半径 r として,
および,n を 3Nとすれば,3N次元の球の体積は,
で与えられます。Γ関数についてはこちらを参考 ⇒ [#] 捕捉2 (21/09/05 加筆) すべての教科書でそのように書いてあるから, 「 同じ空間内を自由に動きまわる同一種類の(古典)気体分子を一つひとつ区別することは意味のないことであることから気体分子数 N!で割って,」と,N!で割ることを当然のように説明した [#] 。つまり,1粒子状態数(または1粒子分配関数)をN乗してN!で割ることでN粒子の状態数(またはN粒子分配関数)が求まるというわけである。このように計算すると,同種粒子の混合エントロピーを計算すると0となる [#] ので,合理的であるという裏付けもある。 では,動き回らない同種粒子からなる固体単結晶の場合,どうであるかというとN!で割る必要はないということになっている。 あなたは納得できるか? 組み合わせを計算するときにn個のうち,n1個同じものがあれば,n1!で割り算をするが,その同じものが動いていれば,それは正しいが,静止していれば,n1!で割る必要はないというように解釈もできる。悩ましい。 ただ,厳密にいうと,この宇宙には古典粒子というものは存在しない。フェルミ粒子とボース粒子の2種類だけである。 よって,悩むことは時間の無駄なのかもしれない。 |
参考:
状態数の数は,
フェルミ統計 ≦ 修正古典統計 ≦ ボース統計 ≦ 古典統計
N!で割ることで, ↑ へ古典統計の状態数を調整している!
[1] 2.で求めた状態数Wを利用すれば,ミクロカノニカルアンサンブルの方法によって,他の熱力学関数を導出することができます。
理想気体のエントロピー
ボルツマンの原理,
S≡klog W(E,ΔE,V,N)
を理想気体の微視的状態数に適用します。微視的状態数,
W(E,ΔE,V,N) = Ω(E)ΔE = 3N W0(E,V,N)ΔE 2E
の両端について対数をとると,
log W = log (3N/2) + logW0 + log (ΔE/E) 〜10 〜1023 〜10
ここで,数モル程度の量が考察の対象であれば,上式の第1項は,粒子数の対数なので10のオーダー,また,第3項は通常のエネルギー状態を区別できるためのエネルギーの測定精度(それ以下のバラツキは見分けられない)を考えれば10桁程度を想定すればよいので,第3項も10のオーダーでしかありません。
一方,第2項は次のように物理的意味を考えます。今は理想気体(=希薄気体)を考えているので,同じ位置に2つ以上の粒子が同時に存在することは想定できない状況であるはずです。したがって,「位置」の状態数だけを考えてもN粒子系の1粒子の取りうる状態数はNより大きくなければならず,N粒子からなる全系の状態数 は,NN (>>N !)より大きいはずです。つまり,N!による修正を受けたとしても,
n! 〜
2πn nne−n スターリングの公式 ⇒ log(NN/N!)〜N/logN
であるから,先の第2項 log W0(E,V,N) はN 程度(以上)の数値をとり,他の項に比べて桁違いに大きいことが分かります。よって,
logW ≒ logW0
と近似しても構いません。つまり,区別がつかないΔEの範囲でエネルギーE とみなせる状態数の対数は,エネルギーE 以下のすべての状態数と等しいとして取り扱っても結果は実質的に同じです。このようなことが成り立つ理由は,「Ω(E) がEに関する急激なとてつもない増加関数 W(E) ∝ E1023 である」ことによります。
[2] したがって,理想気体に対するエントロピーは次のようにも書いても構わないでしょう。
S≒klog W0(E) [理想気体]
先ほど求めたW0(E)の計算結果を代入して,logx ! = x logx - x で近似すれば,(以後,「≒」ではなく,「=」と書きます。)
S = kN 3 log 4πmE +log V + 5 ・・・ [*] 2 3Nh2 N 2
これで,巨視的な量と比較できる熱力学関数の一つ,Sが求まりました。しかし,一つ求めさえすれば,他の熱力学関数は熱力学公式を参照して,次々と計算していくことができます。
| [3] まず,熱力学公式, | ∂S | = | 1 | において,U=<E>=E とみなすことにすれば,[*]より, | |||
| ∂U | V,N | T |
∂S ≡ ∂S =kN 3 ・ 1 = 1 ∂U V,N ∂E V,N 2 E T
したがって,内部エネルギーと温度の関係は,
E = 3 NkT 2
また,この温度Tを用いると,[*]からEを消去して,
S =Nklog V e5/2 2πmkT 3/2 N h2
=Nklog Ve5/2c(T) N
=Nklog Vc(T) + 5 Nk =S(V,T,N) [サッカーテトロードの式] N 2
と表すこともできます。ただし,
c(T)≡ 2πmkT 3/2 ≡ 1 h2 λ(T)3
λ(T)= h 熱ド・ブロイ波長
2πmkT
を定義しました。
圧力,状態方程式
[4] さらに,圧力は熱力学公式と[*]から,
P=T ∂S ∂V E,N
= NkT V
よって,
と書くことができます。もちろん,これは気体の状態方程式と呼ばれる関係式です。
ヘルムホルツ自由エネルギー,化学ポテンシャル
[5] ヘルムホルツ自由エネルギーについては,
F = E−TS
= 3 NkT-T Nklog Vc(T) + 5 Nk 2 N 2
=NkTlog N − NkT Vc(T)
=−NkTlog Ve 2πmkT 3/2 N h2
[6] 化学ポテンシャルも熱力学公式と[*]から直ちに,
μ=−T ∂S ∂N E,V
=−Tk 3 log 4πmE +log V + 5 +TkN 5 ・ 1 2 3Nh2 N 2 2 N
= −kT 3 log 4πmE +log V 2 3Nh2 N
= −kT 3 log 2πmkT +log V 2 h2 N
= kT 3 log h2 +log P =μ(P,T) 2 2πmkT kT
と自然な変数P,Tで表される。
まとめは次のページで
参照: ミクロカノニカルの方法
S(E,V,N) が既知として与えられると,dU=TdS−PdV+μdN から
物理量 計算方法 状態数 量子力学でコツコツ計算 エントロピー S=klogW(E,V,N) 温度
1 = ∂S T ∂E V,N 圧力
P=T ∂S ∂V E,N 自由エネルギー F=E(T,N)−TS(V,T,N) 化学ポテンシャル
μ=−T ∂S ∂N E,V
という熱力学量を計算できる。
W(E,V,N)
[等重率]↓
P(E,V,N)=T ∂S ∂V E,N ← S(E,V,N)=klogW
↓↑
E=U(S,V,N)
自然な変数→
1 = ∂S T(E,V,N) ∂E V,N ↓ ↓ ↓E について解いて ↓
μ(E,V,N)=−T ∂S ∂N E,V E(T,V,N) ⇔ U(T,V,N) →
Cv= ∂U ∂T V,N ↓ → → → ↓
↓ F=E−TS
サッカテトロード式μ(P,T)
自然な変数F(T,V,N)
自然な変数→ ミクロカノニカルアンサンブルの方法
SUSTAINABLE TOKIWADAIGAK SINCE 2002
統計力学 I