t120　強磁性イジングモデル
f-denshi.com  更新日：　13/09/18
サイト検索
目次へ

イジングモデルは強磁性−常磁性転移などをはじめとする，相転移，臨界現象のようなマクロな現象をミクロな道具立てから理解する簡単なモデルです。

１．ブラッグ-ウィリアムズ(Bragg-Williams)近似

この近似では，注目する一つのスピンが感じる場を系の平均値で置き換えて計算を進める。

［１］　総数N個のスピンからなる系が熱浴に接しているとき，ある瞬間の上向きスピンの数をN₊，下向きスピンの数をN_-とします。また，正味の上向きスピンの比率Mを次のように定義し，秩序変数と呼びます。

全粒子数　　　　　N＝N₊＋N_-　　　　　　　　　　　　　　・・・・・(1)

秩序変数　　　　M＝	N+−N-	・・・・・(2)
	N

N+＝N	1＋M	，　　N-＝N	1−M	・・・・・(3)
	2		2

秩序変数Mは，すべてのスピンが上向きのとき，1，上下同数のときはゼロ，すべて下向きのときは-1となり，この系の磁化の相対的大きさを表す量です。

このときの微視的状態の数は，

W＝	N！	・・・・・(4)
	N+！N-！

で与えられます。すると，エントロピーは，

S＝klogW　
  ＝klogN！−klogN₊！−klogN_-！
　＝kNlogN−kN−kN₊logN₊＋kN₊−kN_-logN_-＋kN_-

＝−	Nk		(1＋M)log		1	(1＋M)＋(1−M)log				1	(1−M)		・・・・・(5)
	2				2					2

［２］　ここまでは，常磁性のモデルと同様ですが，ここでは強磁性のモデルを考えるために，隣あわせのスピンの向きによって決まるエネルギーを考慮することにします。

まず，系のエネルギーは，外部磁場H(上方向)とスピン磁気モーメンμ₀との相互作用（エネルギー）は，

−μ₀ H≡−h

で与えられるとすれば，系全体では，

E_H＝−(N₊−N_-)h　

さらに，隣あわせのスピンどおしのスピン相互作用を導入するためにスピン変数として，

σi＝		1　　　　スピン上向き
		−1　　　　スピンが下向き

を定義し，その相互作用を，

−Jσ_iσ_j　，　ただし，J＞0　　　←　スピン方向が同じ向きの方が安定　

と表すことにします。そのとき，スピン相互作用は系全体で，（このページでは z は配位数を意味する。≠exp(μ/kT)絶対活動度ではない）

ES＝−J		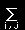σiσj　＝−　(N++＋N--−N+-−N-+)J

となります。ここで，N₊₊，N_--，N_+-，N_-+は隣り合うスピンの向きが，上上，下下，上下，下上である対の数です。

［３］　さらに，隣り合わせのスピンが向きの組がどれだけの数で存在するかは簡潔に表すことはできませんが，ここではブラッグ-ウィリアムズ近似と呼ばれる次の近似を用います。

Ｎ++　〜　 1 N+×z× N+ ＝ zN (1＋M)2 2 N 8 Ｎ--　〜　 1 N-×z× N- ＝ zN (1−M)2 2 N 8 Ｎ+-　〜　 1 N+×z× N- ＝ zN (1−M2) 2 N 8 Ｎ-+　〜　 1 N-×z× N+ ＝ zN (1−M2) 2 N 8

・・・・・(6)

この近似の意味をN₊₊を例に説明しますと，ある上向きのスピンを取り出すとその隣にあるスピンが上向きである確率は系全体における上向きのスピンの割合N₊/Nに等しいと仮定，さらに隣り合う位置にあるスピンの個数である配位数z，「隣どおし」をニ重に数え上げるのを修正するための係数1/2を掛け合わせることで，「隣り合う上向きスピン対の数」N₊₊を見積もっています。一番右の式は(3)式より，N_±を消去しています。他の組み合わせのスピン対の数も同様に近似計算します。

この近似では，上向きスピンの隣りに同じ上向きのスピンが存在する確率は，系全体に含まれる上向きスピンの割合と等しいとしています。しかし，これは現実とはかなり違っています。スピンは上向きどおし，下向きどおしそれぞれドメインを形成しており，上向きスピンの隣りに同じ上向きのスピンが存在する確率は系全体の割合よりずっと大きく，このブラッグ-ウィリアムズ近似の定量性がよくない原因となっています。あなたが陸地のどこかに立っているとき，一歩となりの場所が陸地である確率が，地球上の陸地の割合である２９％ではないことと事情は同じと考えれば理解しやすいでしょう。

以上の記号の下で，外部磁場におかれたN個のスピンからなる系の全エネルギーは，

E　＝　E_H＋E_S

＝−(N+−N-)h −J		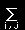σiσj

　　＝　−(N₊−N_-)h−　(N₊₊＋N_--−N_+-−N_-+)J
　　＝　−NhM　−　(N₊₊＋N_--−N_+-−N_-+)J　　　　　　　　　　　　・・・・・(7)

この(7)式に(6)式を代入して，整理すると，

E　＝　−NhM　− 1  zNJM2　　　　　　　　　　　　　　　　　　　　　・・・・・(8) 2

さらにエントロピーとして，(5)を用いて，(ヘルムホルツ)自由エネルギー　F＝E-TS　を計算して，整理すれば，

F　＝　−NhM　− 1  zNJM2　＋NkT 1 (1＋M)log 1 (1＋M)＋ 1 (1−M)log 1 (1−M） 　　　・・・[*] 2 2 2 2 2

が得られます。

外部磁場がないh＝0 の場合

まず，[*]の第１項をh=0として落としてから，臨界温度として，

Tc　＝ zJ 　　　　　　　　　　・・・・・(11) k

を定義して，両辺をNkT_cで割ると，

F	＝−	1	M2＋	T		1	(1＋M)log	1	(1＋M)＋		1	(1−M)log	1	(1−M）		・・・[*]’
NkTc		2		Tc		2		2			2		2

いくつかの温度T/T_cで，この式をプロットすると下図のようになります。

この図からもわかるように低温領域では，M≠0において安定点が２つ存在し，外部磁場がなくてもマクロな磁化を観察することができます。これを自発磁化といいます。

［４］　この境界温度がT_cであることは，[*]’をMで微分して確かめることができます。（まあ，そのようにT_cを定義したわけなんですが，）

1	・	∂F	＝　−M　＋	T	・	log	1＋M	＝0　　　　　　　　　　　　・・・・・(9)
NkTc		∂M		2Tc			1−M

右辺の等式＝を変形していくと，

exp		2TcM		＝	1＋M
		T			1−M

⇔　　　exp		2TcM		−1＝		1＋exp		2TcM		M
		T						T

⇔　　　M＝	exp(2TcM/T)−1	＝	exp(TcM/T)−exp(-TcM/T)	・・・・・(10)
	exp(2TcM/T)＋1		exp(TcM/T)＋exp(-TcM/T)

最後の式を双曲関数を用いて表すと，

M＝tanh Tc M 　　　・・・[**] T

となり，この式の方程式の解が極値をとる必要条件となります。

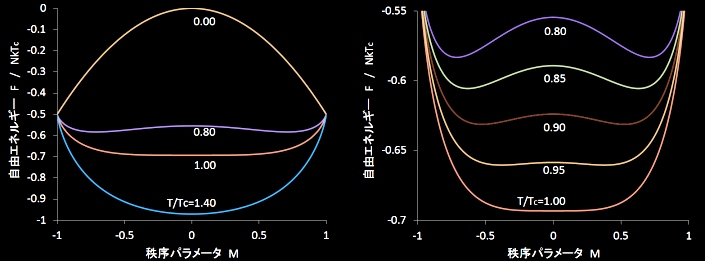
したがって，縦軸をy，横軸をMとして，y＝M　と　y＝tanh		Tc	M				を図示すれば，次のようになり，
		T

この図から確かに，傾き，T_c/T≦1（高温側）であるとき，[**]の解は，M=0　のみであるのに対して，T_c/T＞1（低温側）であれば，M=0　以外にも２つの交点を持つことが分かります。その境界温度はT_cであり，強磁性体がその温度以上で強磁性の性質を消失させるキュリー温度に対応してます。

［５］　h≠0 のときも含めて考えるときは，

M＝tanh Tc M＋ h T zJ

として議論することになりますが，これは h=0 の場合の議論において横軸を平行移動させるだけですから，ここでは説明を省略します。

［６］

平均場近似と呼ばれる理由

もう一度，スピンのエネルギーを考えてみます。

ES＝−J		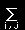σiσj

において，一つのスピン（0と番号を振る）に着目して，

E0＝−Jσ0		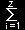σi

を抜き出します。ここで，再隣接スピンの数はz個としています。さらに，総和記号の中のσ_i を系全体のスピンの平均値<σ_i>で置き換えると，

E₀＝−Jσ₀・z<σ_i>

となります。この式から，スピンσ₀ は平均磁場（分子場） ［zJ<σ_i>] と相互作用しているとみなすことができます。

ところが，磁場(=ε)におかれたスピン（=２準位系）の平均エネルギー<E₀>が，

<E0>＝−εtanh	ε
	kT

で与えられること[#]から，磁場を ε⇔［zJ<σ_i>]　と読み替えて，

<σ0>＝	<E0>	/＝−tanh	zJ	<σi>
	ε		kT

でなければならないと推論されます。これは，[**]式と同形の式です。

つまり，ブラッグ-ウィリムズ近似とは，着目するスピン以外のスピンの作り出す磁場を系の平均的な磁場に置き換えて議論をしていることになります。

２．イジングモデルのベーテ(Bethe)近似

［１］　ブラッグ・ウィリアムス近似は注目するひとつのスピンを平均場におく近似ですが，これから説明するベーテ近似は，中心においたスピンと最隣接するｚ個のスピンを含めたクラスターのエネルギーをスピン変数を残したまま計算を進め，残りのスピンについては平均場を適用するところに特徴があります。すなわち，考慮するエネルギー（有効ハミルトニアン）は，

　（１）　中心のスピンは外部磁場H₀と隣接するｚ個のスピンと交換相互作用をする。
　（２）　z個の隣接するスピンは，外部磁場 H₀とクラスター以外のスピンが作り出す分子場 H’と作用する。

となっています。外部磁場と分子場と合わせた有効磁場を　H＝H₀＋H’として数式で書くと，(磁気モーメントは1とした)

E ＝−Jσ0		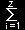σi　−H0σ0−H		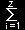	σi

ここで，i に関する和は中心スピン０に最隣接するｚ個のスピンすべてにわたってとることとします。

このエネルギーを用いたカノニカルアンサンブルの方法を適用するために分配関数を求めると，

Z＝		exp		-Ei
				kT

＝	Σ Σ ････ Σ σ0=±1 σ1=±1 σz=±1	exp		1		Jσ0 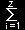σi＋H0σ0＋H 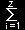σi
				kT

↓　　σ₀についてだけ計算（トレース和，±1をとる）して，

Σ ････ Σ σ1=±1 σz=±1	exp(H0/kT)･exp		J+H	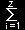σi		＋exp(-H0/kT)･exp		-J+H	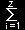σi
			kT					kT

＝exp(H0/kT)

Σ ････ Σ σ1=±1 σz=±1

exp

J+H

(σ1+･･･+σz)

＋exp(-H0/kT)

Σ ････ Σ σ1=±1 σz=±1

exp

-J+H

(σ1+･･･+σz)

kT

kT

ここで，σ_i　について，

	Σ σi=±1	exp		±J＋H	σi		＝2cosh		J±H
				kT					kT

と，i＝1,2,･･･,z　においてすべて同じ計算をすれば，

Z＝exp(H0/kT) 2cosh J+H z ＋exp(-H0/kT) 2cosh J-H z kT kT

一方，

<σ0>≡	1	Σ Σ ････ Σ σ0=±1 σ1=±1 σz=±1	σ0･exp		1		Jσ0 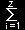σi＋H0σ0＋H 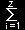σi
	Z				kT

＝	kT	・	∂Z			＝kT	∂	logZ
	Z		∂H0				∂H0

であるから，

<σ0>＝	exp(H0/kT) 2cosh J+H z −exp(-H0/kT) 2cosh J-H z kT kT
	exp(H0/kT) 2cosh J+H z ＋exp(-H0/kT) 2cosh J-H z kT kT

H₀＝0のときは，

＝	cosh J+H z − cosh J-H z kT kT
	cosh J+H z ＋ cosh J-H z kT kT

同様に，H₀＝0のときのσ_i の平均は，（このとき，H=H’である。）

<σi>＝	1	kT		∂Z		H0=0
	z	Z		∂H

＝	cosh J+H z-1 sinh J+H − cosh J-H z-1 sinh J-H kT kT kT kT
	cosh J+H z ＋ cosh J-H z kT kT

ところが，スピンσ₀とσ_iは便宜的に番号を振っただけで，同じものであることから，<σ₀>＝<σ_i> であるはず。すると，

cosh

J+H

z

−

cosh

J-H

z

＝

cosh

J+H

z-1

sinh

J+H

−

cosh

J-H

z-1

sinh

J-H

kT

kT

kT

kT

kT

kT

⇔

cosh

J+H

z-1

cosh

J+H

−sinh

J+H

＝

cosh

J-H

z-1

cosh

J-H

−sinh

J-H

kT

kT

kT

kT

kT

kT

⇔

cosh

J+H

z-1

exp

−

J+H

＝

cosh

J-H

z-1

exp

−

J-H

kT

kT

kT

kT

⇔

exp 2H ＝ kT		cosh J+H kT		z-1
		cosh J-H kT

対数をとって整理すれば，

2H ＝(z−1) kT	log		cosh J+H kT
			cosh J-H kT

2H	＝	log cosh		J+H		−log cosh		J-H
kT(z−1)				kT				kT

ここで，右辺，双曲関数について，J>>Hとして３次の項まで展開した公式[#]において，

log cosh(x±Δx)≒log cosh x ±

sinh x

Δx＋

1

1

(Δx)2 ±

-2

sinh x

(Δx)3

cosh x

2！

cosh2x

3！

cosh3x

x＝J/kT，Δx＝H/kT　とおくと，右辺は奇数次の項だけが残り，

H/kT(z−1)　＝	tanh		J		(H/kT)−	1		sinh(J/kT)	(H/kT)3
			kT			3		cosh3(J/kT)

H≠0　の場合は，(H/kT)で除して，整理すると，（ただし，外部磁場は弱く，H₀<<H’とする。）

1	･	1	(H/kT)2　＝1−	1
3		cosh2(J/kT)		(z−1)tanh(J/kT))

これが解を持つためには，右辺が正でなければならないので，

(z−1)tanh		J		＞１
		kT

これを指数関数に直して，

ex−e-x	＞	1	⇔　e2x＞		z	( x＝J/kT )
ex＋e-x		z−1			z−2

Tについて解けば，，

T＜	2J	･	1	≡Tc　　［転移温度］
	k		log( z/(z-2))

が安定点（解）をもつ条件として得られます。特に，z₀の値は，イジングモデルが1次元の場合は2であり，2次元以上ではそれより大きな値をとります。この式で，正方向から　z₀→ 2　とすると， T_c→0　となりますが，これは次に紹介する１次元イジングモデルの厳密解から得られる値　T_c=0　と一致します。

z>>2のとき，

log	z	＝log	1	≒log（1＋	2	)≒	2
	z−2		1−2/z		z		z

と近似すれば，T_c＝zJ/k　となり，ブラッグ・ウィリアムス近似の結果[#]と一致します。

だいぶ端折っていますが，とりあえず，ここまで。

［目次へ］

SUSTAINABLE　TOKIWADAIGAK　SINCE　2002