|
２ 数列の収束･発散速度 | |
| f-denshi.com [目次] 最終更新日：09/05/08 | ||
| サイト検索 | ||
微分･積分学の教科書はたいてい数列の極限の話から始まります。それは微分･積分の定義に従っていざ計算を始めようとすると数列の極限計算が必要になるからです。しかしながら物理や工学の現場に入ると微分･積分の計算は公式集などをみて済ませる場合がほとんどではないでしょうか。そうかといって，ここを飛ばしてしまうと後々の応用で重要な微分積分の概念の理解に窮することもあるので，この講義でも退屈しない程度に数列の計算方法を簡単にまとめておきました。
［０］ ある条件の下で数を無限に足し合わせていった場合，その合計(＝級数和) が必ずしも無限にならないことは，たとえば，３分の１，これは，
1 ＝0.33333333 ･･････････ 3
と続く無限小数ですが，これを分数で，
1 ＝ 3 ＋ 3 ＋ ････ ＋ 3 ＋ ････ 3 10 100 10n
と書いてみれば，無限級数が，
(１) 3 ＝ 1 10n 3
のように収束することからわかります。もちろん，どのような級数でも収束するわけでなく，少なくとも第 n 項 an が，n→∞ の極限において，
(２) an ＝0
となることが必要です。微分，積分学での議論は，この(１)と(２)のタイプの計算で尽くされるといっても言い過ぎではありません。そして，これらの計算に関するさまざまな定義やテクニックが存在しており，解析学のはじめの方でマスターしておく必要があるのです。
［１］ まず，n→∞ といっても無限大にいく様子はそれこそ無限にあります。たとえば，
n＝ 1 2 3 ･･･ 10 ･･･ an ＝ n 1 2 3 ･･･ 10 ･･･ bn ＝ 10n 10 100 1000 ･･･ 10000000000 ･･･
とでは bn の方が圧倒的に速く無限大にいくだろうと感じます。この無限大にいく速さという感覚は非常に重要で，次のように定義しておきましょう。
|
もちろん，無限大にいく速さにいつも優劣がつくわけでなく，an＝n， bn＝n＋1 ならば，
bn ＝ n＋1 ＝1 (有限の実数) ⇒ an ≒ bn an n
このとき，「無限大にいく速さは等しい。」 ということにします。
［２］ また，n は必ずしも離散的である必要はありません。たとえば，
f(x)＝ 1 ； g(x)＝ 1 x2 x
において，変数 x が連続的にx→∞と変化して，関数値が無限小に至る速度を考えることもできます。このとき，f(x) の 方が g(x) より速く 0 に近づきますが，この状況を，
f(x) ＝ 0 ， または，x→∞ のとき，f(x) ＝ o(g(x)) ． g(x)
と表わし，f(x)は g(x) より高位の無限小であるといいます。ここで，o(g(x)) はランダウ記号とよばれ，しばしば，
” g(x)より高位の無限小である任意の関数 ”
と言う意味でも用いられます。たとえば，
o(h2) (h→0)．
とは，hが0に近づくとき，h2 より高位の無限小の項だけからなる h の関数を意味し，例えば，f(h) ＝ 2h3＋3h5 は o(h2) のひとつです。
したがって，n＜m；a，bを変数hに対して定数とすれば，
a･o(hn)＋b･o(hm) ＝ o(hn)
o(a･hn) ＝ o(hn)
というような集合に基づいた計算が可能です。 ←｛２の倍数の集合｝＋｛４の倍数の集合｝＝｛２の倍数の集合｝というような感じ。
［３］ 次のような代表的な関数の発散速度についてはあらかじめ知っておくと便利です。
|
x → ∞ のときに，無限大にゆく速度： log x << xn << ex << x！<< xxちなみに， x1/x → 1 (x→∞) ← 知っていれば簡単，知らないとチョット難しい |
話の順序が逆になるかもしれませんが，(↓この証明の方がウンと難しい)
n！ 〜
2πn nｎe−n スターリング (n＞10くらい)
の公式［#］は発散速度を知るのに役立ちます。
［１］ 極限の無限大にいく速さに序列があることを利用して極限の計算はおこなわれますが，いつも見てすぐわかるような形をしているわけではありません。そのようなときに役立つのがロピタルの定理です。分数で与えられる関数の極限がすぐにわからないときは，普通，
｜ f(x)｜/｜g(x)｜ → ∞/∞，または，0/0
のような関数形をしていますが，もし，分母･分子を微分した極限，
f’(x) g’(x)
が存在すれば，つぎの定理が成り立ちます。
ロピタルの定理
これを繰り返して用いれば， ここで，f(n)(x) とは f(x) の n階導関数のことです[#]。 |
が成り立ちます。これをロピタルの定理といいます。たとえば，n を自然数として，
xn ex
を考えます。この極限は，x → ∞ のとき，分母，分子 ⇒ ∞ なので，ロピタルの定理を用いて，
xn ＝ nxn-1 ＝ ･･･ ＝ n！ ex ex ex
となり，極限値が自明な(もちろんその値は0です。)右辺にたどり着きます。
この定理，授業では習いませんが，理系の高校生なら，たいてい参考書などで知って いるはずです。
［１］ 収束する数列が，すべて単調に増加しながら，または減少しながらある値に近づいてゆくとは限りません。たとえば，
an＝(-1)n |
1 |
| n |
は，振動しながら0に近づいてゆきます。このように振動する数列の取り扱いに欠かせない概念が，下極限，上極限です。一言で言えば，下極限，上極限とは，「挟み撃ち」のための道具で，面積の計算でも活躍します。
［２］ さて，下極限，上極限の厳密な定義です。ある番号nで，有界な無限数列 ｛xm｝ を前半部分：
M1＝｛x1，x2･･･，xn-1｝
と，後半部分の集合
Mn＝｛xn，xn+1，･･･｝
との２つに分けます。このとき，後半のMnの下限，上限を
Mnの下限＝ xm ， Mnの上限＝ xm
と記述します。ここで，数列｛xm｝に対して，この n → ∞ としたときのこれらの極限をMの下極限，上極限といい，
定義：
|
と書きます。これだけではわかりにくいので例を見てみましょう。(右上図参照 09/05/08訂正)
集合 M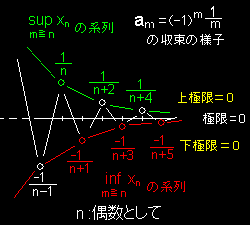 
＝｛am｜am＝(-1)m/m， m＝1，2，3､･･･ ｝を考えます。ここで，数列，
｛an｝＝｛ -1 ， 1 ， -1 ，･･･， (-1)-n ，･･･ ｝ 1 2 3 n
を考えるとこれは 0 に収束します。
M を第 (n-1) 項までとそれ以上の２つの部分，M1∪Mn に分けます。 ここで，
M1＝｛ -1 ， 1 ， -1 ，･･･， (-1)-(n-1) ｝ 1 2 3 n-1
Mn＝｛ (-1)-n ， (-1)-(n+1) ，･･･ ｝ n n＋1
このとき，n が偶数ならば，Mn の
上限： xm ＝1/n
および，
下限： xm ＝-1/(n＋1)
となります。ここで，n→∞ とすると，Mn の
上限の系列： 1 ， 1 ， 1 ， ･･･ n n＋2 n＋4
下限の系列： -1 ， -1 ， -1 ， ･･･ n＋1 n＋3 n＋5
それぞれも 0 に収束していることがわかります。つまり，
［下極限］ lim xn ≦ xn ≦
xn ［上極限］ lim
が一般に成り立つことを利用して極限を上極限と下極限との挟み撃ちにして(下極限と上極限が一致する場合は)極限が求められます。今の例は簡単なので，この有り難味がイマイチですが，ある数列の極限が直接求められないとき，上極限，下極限を求めてそれが一致すれば，極限はその一致した値に等しいと結論することができるのです。
挟み撃ちの方法と不等式
|
(１)ある定数：k＞2a， (1/2)＞(a/k) として，
| an | ＝ |  |
a |  |
|
a | |
･･･ | |
a | |
× | |
a | |
･･･ | |
a | |
| n！ | 1 | 2 | k | k＋1 | n |
| ＜ | |
ak | |
× | |
1 | |
････ | |
1 | |
＝ | |
ak | |
× | |
1 | |
n-k |
| k！ | 2 | 2 | k！ | 2 |
問題：
| (１) |
|
|
［２］ ［ロピタルの定理の証明の概略］
(厳密な証明を追うのは大学生でもたいへん！ ということで，ここではエッセンスだけ．．．)
まず，
f(x) ＝ g(x)−g(a) × f(x)−f(a) ＋ f(a) g(x) g(x) g(x)−g(a) g(x)
と変形しておいて，
↓(右図のような大小関係の場合，α ≦ c ≦ a として，)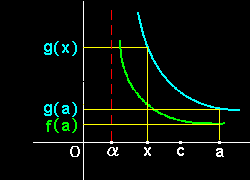
＝ g(x)−g(a) × f’(c) ＋ f(a) g(x) g’(c) g(x)
＝ 1− g(a) f’(c) ＋ f(a) g(x) g’(c) g(x)
と式の変形を行います。ここで，x →α と同時にa も a → α としますが，そのとき，
g(a) → 0， f(a) → 0 g(x) g(x)
が成り立つようにx がα に近づく速度を，a がα に近づく速度よりも十分速いようにすることができるはずです。
x →α >> a →α
もちろんこのとき，c →α となるので，f’(c)／g’(c) → f’(α)／g’(α)，結局，
f(x) ＝ f’(x) g(x) g’(x)
となるであろうと推測できます。
