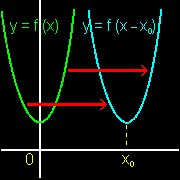|
4 テイラー展開 |
|
| f-denshi.com [目次] 更新日:03/11/13 |
| サイト検索 |
|
1.テイラーの定理
[1] ここでは,無限回微分可能な関数: f(x) を有限,または無限項の多項式[#] で近似する方法を考えましょう。例えば,指数関数は,
| (I) ex=1+ |
1 |
・x+ |
1 |
・x2+・・・+ |
1 |
・xn-1+ |
eθx |
・xn |
; (0<θ<1) |
|
|
|
|
| 1! |
2! |
(n−1)! |
n! |
または,
| (II) ex=1+ |
1 |
・x+ |
1 |
・x2+・・・+ |
1 |
・xn-1+ |
1 |
・xn + ・・・ |
|
|
|
|
| 1! |
2! |
(n−1)! |
n! |
と表されます。
(I) のように書けることを,テイラーの定理,
(II) のように書けることをテイラー級数展開(または,テイラー展開)
が可能である言います。一般の関数についてきちんと書くと次のようになります。
[ テイラーの定理 ]
閉区間 [a,b] で n 回微分可能な関数 f(x) とすれば,
θ (0<θ<1) が存在して,
| f(b)=f(a)+ |
f'(a) |
(b−a)+ |
f''(a) |
(b−a)2+・・・+ |
f(n-1)(a) |
(b−a)n-1+ |
f(n)(a+θ(b−a)) |
(b−a)n |
|
|
|
|
| 1! |
2! |
(n−1)! |
n! |
|
証明はロルの定理(平均値の定理)と同じですが多少ややこしいです。⇒[#]
[ テイラー級数展開可能とは ]
閉区間[a,b]で無限回微分可能な関数f(x)とすれば,n→無限の極限において,
| f(b)=f(a)+ |
f'(a) |
(b−a)+ |
f''(a) |
(b−a)2+・・・+ |
f(n-1)(a) |
(b−a)n-1+ |
f(n)(a) |
(b−a)n+・・・ [*] |
|
|
|
|
| 1! |
2! |
(n−1)! |
n! |
とできる。 (等号が成立する。) |
ここで,a=0 の場合をマクローリン展開[#]と呼んで区別することもあります。)
[2] よく使うテイラーの定理の別形は,b=x,または,a→x,b→x+h と置き換えて,
| (1) f(x) = f(a)+ |
f'(a) |
(x−a)+ |
f''(a) |
(x−a)2+・・・+ |
f(n)(a+θ(x−a)) |
(x−a)n |
|
|
|
| 1! |
2! |
n! |
| (2) f(x+h) = f(x)+ |
f'(x) |
h+ |
f''(x) |
h2+・・・+ |
f(n)(x+θh) |
hn |
|
|
|
| 1! |
2! |
n! |
|
さらに最後の項を積分形にして,(n+1回微分可能とした形で書くと,)
| (3) f(x)=f(a)+ |
f'(a) |
(x−a)+ |
f''(a) |
(x−a)2+・・・+ |
f(n)(a) |
(x−a)n+ |
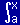 |
f(n+1)(θ) |
(x−θ)ndθ |
|
|
|
|
| 1! |
2! |
n! |
n! |
|
も重要です。
[3] さて,これらの定理の内容について考えて見ましょう。まず,関数:f(x)が有限な多項式:
f(x)=c0+c1(x−a)+c2(x−a)2+・・・・+cn(x−a)n : aは定数
であったとします。(この場合,''展開''する意味はないのですが,・・) これを k 回微分して,x=a とおくと,
f(k)(x)=k!ck+・・・+n(n-1)・・・(n-k+1)cn(x−a)n-k
| f(k)(a)= |
 |
k!ck (k=0,1,・・・,n) |
| 0 (k=n+1,・・・,∞) |
|
⇒ |
| ck= |
 |
|
| 0 (k=n+1,・・・,) |
|
なので,
| f(x)=f(a)+ |
f'(a) |
(x−a)+ |
f''(a) |
(x−a)2+・・・+ |
f(n)(a) |
(x−a)n+0+0+・・・ |
|
|
|
| 1! |
2! |
n! |
| =f(a)+ |
 |
f(k)(a) |
・(x−a)k |
|
| k! |
であることがわかります。以上の考察から,有限項で表せるとは限らないn回(以上)微分可能な一般的な関数については,
| f(x)=f(a)+ |
f '(a) |
(x−a)+ |
f ''(a) |
(x−a)2+ ・・・ + |
f (n)(a) |
(x−a)n+R(x) |
|
|
|
| 1! |
2! |
n! |
と書いても的外れではないでしょう。このR(x)を剰余項(remainder)といいます。もちろん,R(x)が有限な範囲で定まるかどうかなどわからないのですが,テイラーの主張することは,ある関数は,「n
をどんどん大きくしてゆくと,この剰余項はいくらでも0 に近づけることができる。」ということなのです。
[4] 今度は(3)について説明します。この式は微分積分法の基本公式[#];
| F(x)−F(a)= |
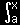 |
f(θ)dθ |
|
⇒ |
| f(x)−f(a) = |
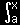 |
f'(θ)dθ |
|
| 記号を改め |
をよくみると,これは(3)においてn=0 とした場合であることがわかります。そこで,これを部分積分してみましょう。
| f(x)=f(a)+ |
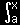 |
1・f'(θ)dθ |
| =f(a)+[ |
−(x−θ)f'(θ)] |
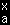 |
− |
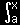 |
{−(x−θ)f''(θ)}dθ |
| =f(a)+(x−a)f'(a)+ |
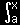 |
(x−θ)f''(θ)dθ |
| ここで, |
d |
{−(x−θ)}=1 を利用しています。引き続き, |
|
| dθ |
| d |
{−(x−θ)k+1}=(k+1)(x−θ)k ; k = 1,2,・・・ |
|
| dθ |
を利用して部分積分を繰り返すと(3)が得られ,これが証明になっていることがわかります。
[5] では,上のように微分積分法の基本定理の部分積分を繰り返すときに積分変数記号を変えながら行うとどうなるでしょうか。つまり,
| f(x) =f(a)+ |
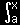 |
f'(x1)dx1 |
| f'(x1)=f'(a)+ |
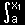 |
f''(x2)dx2 |
| f''(x2)=f''(a)+ |
 |
f(3)(x3)dx3 |
| : |
| f(n-1)(xn-1)=f(n-1)(a)+ |
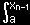 |
f(n)(xn)dxn |
を逐次下から上に代入していくのです。まず,二番目の式を一番目の式に代入すると,
| f(x) = f(a)+ |
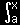 |
{f'(a)+ |
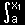 |
f''(x2)dx2}dx1 |
| f(x) = f(a)+f'(a) |
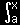 |
dx1+ |
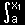 |
f''(x2)dx2dx1 |
| = f(a)+f'(a)(x−a)+ |
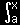 |
 |
f''(x2)dx2dx1 |
となります。次は3番目の式 f''(x2)=・・・をこの被積分関数のところに代入します。・・・。これを繰り返すと,
| (4) f(x)=f(a)+ |
f '(a) |
(x−a)+・・・+ |
f (n-1)(a) |
(x−a)n-1+ |
  |
・・・ |
 |
f(n)(xn)dxn・・・dx2dx1 |
|
|
| 1! |
(n-1)! |
|
となります。量子力学(時間発展問題など)で積分記号がたくさん並んでいたら,たいていこの公式とにらめっこです。[#]
[6] 剰余項についてもう一度書くと,
| R(x)=f(x)−{f(a)+ |
f'(a) |
(x−a)+ |
f''(a) |
(x−a)2+・・・+ |
f (n)(a) |
(x−a)n} |
|
|
|
| 1! |
2! |
n! |
となります。これをn+1回微分すると,{ }の項は0となり,
| dn+1 |
R(x) = |
dn+1 |
f(x) |
|
|
| dxn+1 |
dxn+1 |
という関係が存在していることがわかります。
2.マクローリンの定理
テイラーの定理において,原点 0 のまわりに関する展開をマクローリンの定理と呼びます。
[マクローリンの定理・展開]
閉区間[0,b]でn回微分可能な関数f(x)とすれば,0≦x≦bに対して, θ(0<θ<1) が存在し,
| f(x)=f(0)+ |
f'(0) |
x+ |
f''(0) |
x2+・・・+ |
f(n-1)(0) |
xn-1+ |
f(n)(θx) |
xn |
|
|
|
|
| 1! |
2! |
(n−1)! |
n! |
もしくは,マクローリン級数,
| f(x)=f(0)+ |
f'(0) |
x+ |
f''(0) |
x2+・・・+ |
f(n-1)(0) |
xn-1+ |
f(n)(0) |
xn+・・・ |
|
|
|
|
| 1! |
2! |
(n−1)! |
n! |
と表される。 |
まず,この定理,b<0 でも|b|=∞ でも成り立つのです! 特に,[0,∞),(-
∞,0]の両区間で成り立つときは,実数全体で成り立ちます。
例えば,指数関数,f(x) = ex を考えましょう。この関数は -∞ ≦ x ≦ ∞ で n 回(実は無限回なのですが)微分可能です。したがって,マクローランの定理は任意の実数 x に対して,あるθが存在して,
| ex=1+ |
1 |
・x+ |
1 |
・x2+・・・+ |
1 |
・xn-1+ |
eθx |
・xn |
|
|
|
|
| 1! |
2! |
(n−1)! |
n! |
=exp(x)
となることを保障します。もちろん,すべての実数に対してもテーラー展開可能です。
3.具体的計算:
具体例をいくつか紹介しましょう。実践的には公式集をみればいいことなのですが,いくつかは暗記しておいて損はありません。
例1 有理関数
| (1) |
1 |
=1−x+x2−x3+x4−・・・ (-1<x<1) |
|
| (1+x) |
| (2) |
1 |
=1−2x+3x2−4x3+5x4−・・・ (-1<x<1) |
|
| (1+x)2 |
| (3) |
1 |
=1− |
1 |
x+ |
1・3 |
x2− |
1・3・5 |
x3+・・・ (-1<x≦1) |
|
|
|
|
|
|
 |
1+x |
|
2 |
2・4 |
2・4・6 |
対数関数
| loge(1+x)=x− |
1 |
x2+ |
1 |
x3− |
1 |
x4+・・・ (-1<x≦1) |
|
|
|
| 2 |
3 |
4 |
例2 今度はすこし高級な雰囲気のする応用です。テイラー級数展開[*]において,b=x-x0, a=x とおけば,
| f(x-x0) = f(x)+ |
f'(x) |
(-x0)+ |
f''(x) |
(-x0)2+・・・+ |
f(n)(x) |
(-x0)n +・・・ |
|
|
|
| 1! |
2! |
n! |
| = f(x)+ |
-x0 |
d |
・f (x)+ |
(-x0)2 |
d2 |
・f(x)+・・・+ |
(-x0)n |
dn |
・f(x)+・・ |
|
|
|
|
|
|
| 1! |
dx |
2! |
dx2 |
n! |
dxn |
↓ ここで,演算子: px =−ih |
d |
,つまり, |
d |
= |
i px |
と置き換えると, |
|
|
|
| dx |
dx |
h |
| = f(x)+ |
(-i pxx0/h) |
・f(x)+ |
(-i pxx0/h)2 |
・f(x)+・・・+ |
(-i pxx0/h)n |
・f(x)+・・ |
|
|
|
| 1! |
2! |
n! |
| = |
 |
1 + |
(-i pxx0/h) |
+ |
(-i pxx0/h)2 |
+・・・+ |
(-ipxx0/h)n |
+・・ |
 |
・f(x) |
|
|
|
| 1! |
2! |
n! |
| = exp |
 |
(-i pxx0) |
 |
・f(x) |
|
h |
すなわち,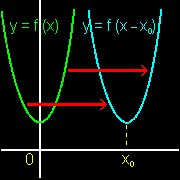
| exp |
 |
(-i pxx0) |
 |
f (x) = f(x-x0) |
|
h |
|
これは演算子:exp[・・] が f(x) に作用して,その結果 f(x) が正方向へ平行移動した
f(x-x0) が得られることを示しています(右図参照)。これは量子力学で,平行移動演算子と呼ばれるものです。
同様に,テイラー展開で,b=t+t0,a=t,H=ih |
∂ |
とおけば,←符号に注意 |
|
| ∂t |
| exp |
 |
(-i Ht0) |
 |
f (t)=f(t+t0) |
|
h |
|
の関係が得られます。この指数関数は量子力学で時間推進演算子と呼ばれるものです。 変数 t を時刻と見れば,関数f(t)に exp[ ]が作用して,t0 だけ時間が進んだときの関数 f(t+t0) が得られることを示しています。ちょっと深遠な名前ですが,単なるテイラー展開なんです。
[ 目次へ ]
補足
テイラー展開できない関数の話:
| f(x)= |
 |
exp (-x-2) (x>0) |
| 1 (x≦0) |
は x=0 の周りで展開できません。 実際,この関数を微分すると,
f'(x) = 2x-3 ・exp (-x-2) ⇒ f'(0) = 0
高階微分も,f(n)(0)= 0 なので,公式どおりテイラー展開すると,
f(0+Δx) = 1 + 0 + 0 + ・・・
となってΔx の高次の項が出てきません。もちろん,この f(0+Δx) = 1 は大ウソ。
X〜0 のところの f(x) を近似しようとしても,この関数はどんな 1+xn より速く 1に近づくので多項式では近似できないのです。