| 10 ラグランジュの未定乗数法 | ||
| f-denshi.com [目次] 最終更新日:04/06/13 | ||
| サイト検索 | ||
[1] 問題:「半径1の球に頂点が内接する直方体の体積が最大となるのはどのようなときか?」
を言い直すと, x,y,z > 0 を定義域とする,(図は下の汚いやつを見てください[#])
「関数 f(x,y,z) = 8xyz の最大値を,条件 g(x,y,z) = x2+y2+z2−1 = 0 のもとで求めよ。」
となります。このような問題を条件付き極値問題といいます。この問題では変数が3つ出てきますが,条件式 g(x,y,z) = 0 を z について解き, f に代入し z を消去すれば,2変数関数の極値問題に帰着して解くことができます。←つまり,この問題で真に独立な変数のカズは2つです。しかし,この変数を減らすやり方では,g(x,y,z) が複雑な形で,一つの変数について解けない場合行き詰まってしまいます。そんな場合も含めてこの問題の形式解を得る方法として,ラグランジュの未定乗数法(ラグランジュの未定係数法ともいいます)があります。似かよったテクニックに陰関数定理⇒[#]というのもありますので,参考にしてください。
[2] ここでは,問題をもう少し一般化し,
「3変数関数:f(x,y,z)が拘束条件:g(x,y,z)=0 のもとで,極値をとる必要条件を求めよ。」
として説明しましょう。まず,関数 f(x,y,z) が,x=x0,y=y0,z=z0 において極値をとる必要条件は,その点で任意の dx,dy,dz について,
(1) df= ∂f dx+ ∂f dy+ ∂f dz = 0 ∂x ∂y ∂z
↑ δf= ∂f δx+ ∂f δy+ ∂f δz = 0 とも書きます。 ∂x ∂y ∂z
が成り立つことです。さらに条件:g(x,y,z) = 0 より,
(2) dg= ∂g dx+ ∂g dy+ ∂g dz=0 ∂x ∂y ∂z
が同時に成り立つことも必要です。この2式は連立方程式を加減法[#]で解くときと同じように,(2)に適当なλをかけて(1)と足し合わせれば,変数 ” dz ” の項を消去でき,2つの独立変数 x,y の式にできるはずです。つまり,
∂f +λ ∂g = 0 ・・・・・ ( I ) ∂z ∂z
となるようにλを選べば,(1)+λ・(2)は,
(3) ∂f +λ ∂g dx+ ∂f +λ ∂g dy = 0 ∂x ∂x ∂y ∂y
となります。一方,この式が独立な2つ変数の任意の変化量 dx,dy に対して常に 0 となるのは dx と dy の係数 = 0 のときです。結局,( I )と次の2式とをあわせた3つの対称的な式:
∂f +λ ∂g =0 ・・・・・( II ) ∂x ∂x
∂f +λ ∂g =0 ・・・・ ( III ) ∂y ∂y
を
g(x,y,z)=0 ・・・・・ (IV)
のもとで解くことになります。 ←(IV)は(2)で代用できませんぞ。お忘れなく。
[3] ところが,これら( I ),( II ),( III ),(IV)は次の4変数関数:h(x,y,z,λ)
h(x,y,z,λ)=f(x,y,z)+λg(x,y,z)
が極値をとる必要条件とも見なせることに気付きます。つまり,h(x,y,z,λ) の各変数での偏微分が 0 に等しいとする4つの式は,まさに( I )〜(IV)と同じですね!
(λは一般的に x,y,z の関数ですが,あくまでも h は,x,y,z とλの4つの変数の関数とみなすところがミソなんです。)
[4] 変数が多くなった場合も同様で,このような変数λを導入して条件付極値問題を解く方法をラグランジュの未定乗数法と言います。
| ラグランジュの未定乗数法 1. n変数関数: f(x1,x2,・・・,xn) が拘束条件:g(x1,x2,・・・,xn)=0 のもとで極値をとる必要条件は,適当なλを変数に加えた(n+1)変数関数: h(x1,x2,・・・,xn,λ)=f(x1,x2,・・・,xn)+λg(x1,x2,・・・,xn) が極値をとる必要条件に等しい。 2. 拘束条件が,g1(x1,x2,・・・,xn)=0,・・・,gm(x1,x2,・・・,xn)=0,と m 個ある場合は, 適当なλjを変数に加えた(m+n)変数関数: h(x1,x2,・・・,xn,λ1,・・,λm)=f(x1,x2,・・・,xn)+λ1g1(x1,x2,・・・,xn)+・・・+λmgm(x1,x2,・・・,xn) が極値をとる必要条件 ( m+n個の方程式) に等しい。(ただし,m<n ) |
[1] ラグランジュの未定乗数法を用いて,この章のはじめに示した問題を解いて見ましょう。 それは,1. において,
g(x,y,z) =x2+y2+z2−1=0
f(x,y,z) =8xyz
とすればよく,x,y,z,λの関数,
h(x,y,z,λ) = 8xyz+λ(x2+y2+z2−1)
の極値を求めることになります。各変数で偏微分して,それを0とおけば,連立方程式
∂h = ∂f +λ ∂g = 8yz+λ・2x = 0 ・・・・・(1) ∂x ∂x ∂x
∂h = ∂f +λ ∂g = 8zx+λ・2y = 0 ・・・・・(2) ∂y ∂y ∂y
∂h = ∂f +λ ∂g = 8xy+λ・2z = 0 ・・・・・(3) ∂z ∂z ∂z
∂h = g(x) = x2+y2+z2−1 = 0 ・・・・(4) ∂λ
が得られます。この連立方程式(未知数=式の数=4 )の解は,x=y=z= 1/31/2,λ=- 4/31/2 と求まり,
一辺の長さが,
2 ,体積 V = 8
3
3 3
である立方体というのが問題の答えとなります。
[2] この条件付き極値問題を幾何学的な視点で考えてみます。(21/5/11 加筆)
それは,「2つの曲面
g(x,y,z) =x2+y2+z2−1=0
f(x,y,z) =8xyz=V
が交わっているという条件の下で,V の最大値を求める。」
ことを考えることになります。
曲面 f(x,y,z)=V (一定) の概形を図示する(形状を分かりやすくするため第一象限以外も示している)と,
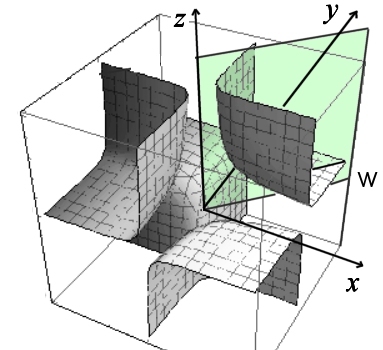
のようになります。これに半径1の球面を書き加え,V>0 をいろいろ変化させて,2つの図形が交わる範囲内で V の最大値を求めればよいわけです。
第一象限の平面 x=y の断面図を図示すると下のとおりとなります。
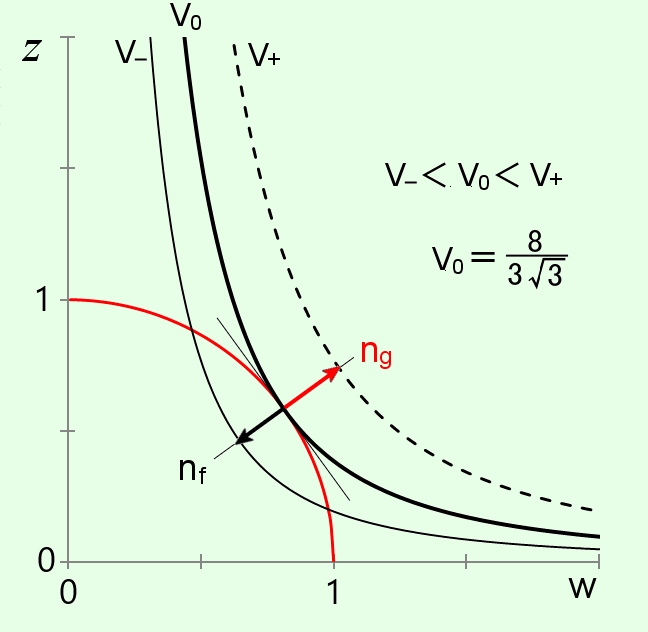
この図から,V がある V0以下であれば,2つの曲面は交わっていますが,これより大きな V の値では2つの曲面が交わらないことが見て取れます。
つまり,2つの曲面が接するときにV が最大値をとることが分かりますが,そのときは,曲面 f=0 と g=0 の接点における法線は,同一直線上になければいけません。
その条件は,各曲面の法線ベクトル,
G = ∂g , ∂g , ∂g ∂x ∂y ∂z
F = ∂f , ∂f , ∂f ∂x ∂y ∂z
が (−λ) を実数として,F =−λG の関係を満たすことです。すなわち,
∂f +λ ∂g = 0 ∂x ∂x
∂f +λ ∂g = 0 ∂y ∂y
∂f +λ ∂g = 0 ∂z ∂z
これらは未定乗数法で解いたときに現れた(1),(2),(3)式と同じです。
また,接点は g(x)=0 上にあるので,
g(x) =x2+y2+z2−1 = 0 ・・・・(4)
も満たしていないといけません。
結局,幾何学的に考えても解くべき連立方程式は,未定乗数法で考えるときと同じだということが分かります。
補足: この問題の答案は,統計力学の教科書によく書かれている書き方にならえば,関数
h(x,y,z,λ) = 8xyz+λ(x2+y2+z2−1)
の極値は,この関数の微分(=変分ともいいます),
δh(x,y,z,λ) = δ(8xyz)+δλ・(x2+y2+z2−1)+λ・δ(x2+y2+z2−1)
=(8yz+2λx)δx+(8zx+2λy)δy+(8xy+2λz)δz+(x2+y2+z2−1)δλ
を考えて,
” 独立な変数 δx,δy,δz,δλ について,「 δh=0 」 が成り立つためには,その微分量の係数がゼロでなければならない。 ”
ということから,連立方程式:(1)〜(4) を得ることになります。