9-2　多変数関数の極値問題
f-denshi.com    [目次]　最終更新日：
サイト検索
多変数関数の微分係数を計算する最大の目的は，１変数の場合と同様に関数の最大値や最小値を具体的に求めることにあります。ここでは，２変数関数についてだけ説明します。　　　　　

１．　２変数関数の極値問題

[１]　２変数関数のテイラー展開を利用して，２変数関数の極値問題を考えてみます。考え方は１変数の場合と同じです。

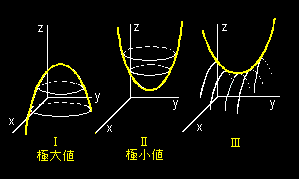　２変数のC2級関数　z ＝ f(x，y) が，(x，y) ＝ (a,b) で極値をとる必要条件は１変数の場合と同様に１階微分係数が(a,b) で 0 となることです。特にx軸，y軸に沿った偏微分，

　(1)　　 ∂f (a,b)＝0，　 ∂f (a,b)＝0
∂x ∂y
が成り立つことが必要です。
　右図の I と II のような状況では (1) をみたしており，z ＝ f(x，y) は極大値，または極小値とをとります。しかし，右図の III の状況では(x，y) ＝　(a,b) で (1) をみたしているにもかかわらず，関数は極値を取りません。つまり，(1)　は極値をもつ十分条件ではないのです。1変数関数でいうところの変極点なのです。
　　　　((1) は停留条件といわれます。)

[２]　この状況をさらに詳しく調べるためにはテイラーの展開式の２次の項を見なければなりません。(1) が成り立っているとき１次の項は0なので2次の項だけ残り，

f(a＋h,b+k)−f(a,b)
　　　　  ＝ (1/2)[h2fxx(a＋θh,b+θk)＋2hkfxy(a＋θh,b+θk)＋k2fyy(a＋θh,b+θk)]

　　　　　　↓　　　k ≠ 0 として，X ＝ h/k　と置き換えをすると，

 ＝ (k2/2)[AX2＋2BX＋C]　≡ Y(X)

ただし，

A ＝ fxx(a+θh,b+θk)
B ＝ fxy(a+θh,b+θk)
C ＝ fyy(a+θh,b+θk)

と書けます。Y(X)の値が正であるか負であるかの判定は，X に関する２次方程式の判別式： D ＝ B2−AC を用いて行うことができます。　  (この辺は高校生のときにも勉強してますね。)

[３]　すなわち，

(a)　D＜0　

ならば，Xの２次関数Y=Y(X)はX軸と交わらないので，

(a1)  A＞0 のとき　　⇒　常にY(X)＞0　⇒　常に f(a＋h,b+k)−f(a,b) ＞0　
(a2)  A＜0 のとき　　⇒　常にY(X)＜0　⇒　常に f(a＋h,b+k)−f(a,b) ＜0

がわかります。つまり，(a) かつ (a1) で極小値，(a) かつ (a2) で極大値をとります。

 なおこの判別式中の A，B，C は，fxx，fxy，fyyが連続(C2級関数を仮定)なので，h，k が十分小さいとき， (a+θh,b+θk) での値の代わりに (a,b) での値を用いることができます。すなわち，

　停留点が極値となる十分条件　

　・極小値をとる：
　　fxx(a,b) ＞ 0，かつ　{fxy(a,b)}2−fxx(a,b)･fyy(a,b) ＜ 0

　・極大値をとる：
　　fxx(a,b) ＜ 0，かつ　{fxy(a,b)}2−fxx(a,b)･fyy(a,b) ＜ 0

　判別式が　(a)　D＜0　以外の場合ですが，

(b)　D＞0　ならば，Y(X)は正，負両方の値をとるので (a,b) で極値をとらないことがわかります。

(c)　D＝0　ならば，何もいうことができないので，さらに高次の項を考える必要があります。⇒ [#]　

[４]　一般的なn変数C2級関数が極値となる十分条件は，ヘッセ行列と呼ばれる次のような行列

H＝ f11･・・･･11n
，　fij＝ 　∂2f ＝ 　∂2f ＝fji
∂xi∂xj ∂xj∂xi
f21･････f2n
　････････
fn1･････fnn

を考え，その固有値の符号で判断されることとなります。その理解には固有値論の知識が必要です(大学１年生には難しいかも) ので，こちらを参考にしてください。
⇒　［#］


[ 目次へ ]