
 |
7 コーシーの積分公式 | |
| f-denshi.com [目次へ]最終更新日: | ||
| サイト検索 | ||
[1] コーシーの積分定理から引き続いて導かれる定理を見ていきましょう。
| 定理 単一閉曲線C0の内部にもう一つ単一閉曲線C1があって,この二つの閉曲線が囲む領域Dにおいて関数f(z)が正則ならば, である。 |
 この定理は積分値に影響を与えないように積分経路を縮小してゆく際に役立ちます。
この定理は積分値に影響を与えないように積分経路を縮小してゆく際に役立ちます。
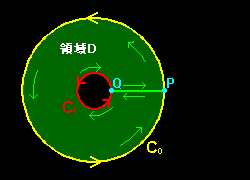
証明は右図において,正則な領域 D を常に進行方向の左に見るような:
「Pから出発し,C0 を正方向に1周して P に戻り → 線分PQ → Q から C1を負の方向に1周してQに戻り→線分QPを通って起点Pに戻ってくる」
という閉じた経路C[#]についてコーシーの積分定理[#]を適用すると,
| 0 = | f(z)dz= | f(z)dz+ | f(z)dz+ | f(z)dz+ | f(z)dz | |||||
ここで,
(1) 第2項,4項 (線分 PQ 上の積分) がキャンセルし合うことと,
(2) C1 の積分経路が逆向き(負方向)の −C1 であること
ことに注意すれば,
0 = f(z)dz− f(z)dz
が得られます。
[1]上の定理からさらに次の定理が得られます。
| 定理 コーシーの積分公式 (1) 領域 D 内で正則な関数 f(z)とするとき,D内の点a のまわりを正方向に一周する単一閉曲線を Cとすると, (2) 点 a を領域内の任意の点,z∈D にとれることを強調して, (3) 特に a=0 のとき,
|
a=0 のときの(3),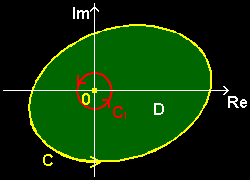
f(0)= 1 f(z) dz 2πi z
の証明の考え方を示し,この定理の意味を考えてみましょう。まず,z=0以外で,関数 f(z)/z が正則なので,1.の定理 [#] から,中心が0,半径が十分小さな正数 δ>0 である円周 C1 を新しい経路としても積分の値は変わりません。すなわち、
f(z) dz= f(z) dz z z
[2] また,f(z) がD で正則なので,f(z) は D で連続です。つまり,任意の δ に対してある ε が存在して,
|z|<ε のとき, |f(z)−f(0)|<δとすることができる。
↑ (z→0 のとき,f(z)→f(0)ということ
とできます。積分経路を半径 δの円周上とし,それを極表示で, z=δ exp(i θ) とすれば,次の積分は,
| f(z)−f(0) | dz | = | f(z)−f(0) | ・i δ exp(i θ)dθ | ← dz=iδexp(i θ)dθ | ||||||
| z | δ exp(i θ) |
≦ f(z)−f(0) dθ
< δ dθ=2πδ
と見積もることができます[#]。よって,δ→0 の極限では,
f(z) dz−f(0) 1 dz=0 z z
↑ f(0)は定数として,積分の外に出しました。
となります。
[3] さらに第2項の積分は,
1 dz= 1 ・i δ exp(i θ)dθ=2πi z δexp(i θ)
と積分できます。結局,定理の(3)が成り立つことがわかります。
[4] 原点以外の点a の場合は,点a を中心とする小さな円を考えれば良いこと容易にわかります。ポイントは
(1)積分結果に影響を与えず,積分経路をいくらでも a の近傍に変形できる。
(2)正則な領域では,a'が a の近傍にあれば,f(a)=f(a')とみなせる[連続性]。
ということです。つまり,a の極近くの経路上で積分するときには被積分関数の分子
f(t)は定数 f(a)として積分の外に出してかまわないということです。
[1] 積分定理を aの関数とみなして n 回微分すると次の公式が成り立ちます。
| 定理 n階微分の積分表示 領域 D内で正則な関数 f(z)とするとき,D内の点 a のまわりを正方向に一周する単一閉曲線 C をとするとき,
|
[2] 完全な証明は数学的帰納法を使いますが,ここでは n=1 のときだけ示しておきます。コーシーの積分公式[#]より,
2πi f(a)= f(z) dz z−a
2πi f(a+h)= f(z) dz z−(a+h)
を辺々引き算して,h で割り,h→0 の極限を考えれば,
2πi f(a+h)−f(a) = f(z)h dz h (z−a−h)(z−a)h
極限 h→0 と積分の順序を入れ換えて,
2πi f'(a)= f(z) dz (z−a)2
とできます。
[3] n≧2 の場合は上と同様な計算を数学的帰納法に用いて証明できます。