| 8 測度空間と可測関数 | ||
| f-denshi.com [目次へ] 最終更新日: 04/12/19 (メモ) | ||
| サイト検索 | ||
リーマン積分は,面積が自明な細長い短冊(長方形)の寄せ集めを用いて,連続関数で囲まれる面積を近似することから始まりますが,ルベーグ積分は,測度が自明な特性関数の寄せ集めで可測関数を近似することから始めます。
集合 X + ボレル集合体 β ||| 可測空間 (X,β) 特性関数 → ↓ ↓ ← 測度 m 可測関数 測度空間 (X,β,m) ↓ ルベーグ積分論
このページでは,ここまでの話を整理しながら,ディリクレ関数以外の一般的な可測関数の積分に必要な単関数について説明します。
[1] 測度空間の定義です。
|
測度の定義1: 集合 X に対してσ集合体[#]β を定め,これを可測空間 (X,β)といいます。 このとき,関数 (=集合関数), m : β → R+=[0,∞] が測度であるとは次の条件を満たすことである。 (1) m(φ) = 0 (2) 可測集合列,A1,A2,・・・∈β が互いに共通部分を持たない(互いに素)ならば, この測度の定められた可測空間を,測度空間 (X,β,m) という。 |
特に m(X)<∞ のときは有限測度,さらに m(X) = 1 のときは,確率測度と言い, 確率空間 (X,β,m) ともいいます。
5 ボレル集合体 に挙げた”正四面体のサイコロ” は確率空間の例です。なお,確率空間に対しては,(Ω,F ,P) という記号がしばしば用いられます。
集合列の極限 について,7上・下極限集合とファトゥーの補題 にまとめておきましたので,そちらも読んでください。
特に(2)から,A⊂B であるならば,
m(B−A)=m(B)−m(A)
も成り立ちます。
[1] 可測関数の定義です。
|
定義: 可測関数 可測空間 (X,β) と X 上の実数値(±∞含む)をとる関数 f(x)とが与えられていて,任意の実数 a,b ( a<b ) に対して X0≡{x|a ≦ f(x)<b} ∈ β であるとき,f は可測関数 (またはβ-可測) であるという。 |
ボレル可測関数はルベーグ可測関数でもあります。普通に思いつく関数はどれも上の定義を満たしていて当たり前で,可測でない関数の例を探し出すほうが大変です。可測関数のイミを理解する一番の方法は位相空間 (ユークリッド空間) おける連続関数と対比することです。可測関数とは一言で,「完備ではない連続関数の集合」を完備化して得られた,「完備な関数の集合」(の元)というイメージで捉えることができます。
理解を助けになるよう下に比較一覧を書いておきます。
| 空間 | 連続関数 | 可測関数 | ||||||||||
| 数にたとえたイメージ! | 有理数(完備でない)みたいなもの | 実数(完備)みたいなもの | ||||||||||
| 具体的関数 | g(x)=0 | ディリクレ関数 ∈ g(x)=0 a.e. | ||||||||||
| 定義される空間 | 位相空間 ( 距離空間でもOK ) | 可測空間 | ||||||||||
| 空間を定める集合族 | 開集合族 O | σ(ボレル)集合体 β | ||||||||||
|
|
|||||||||||
| 定義 |
任意の実数 a,b (a<b) に対して, |
任意の実数 a,b (a<b) に対して, |
||||||||||
| リーマン積分 | 可能 | 可能とはかぎらない | ||||||||||
| a・f+b・g, f・g, |f| | f,g が連続関数ならば, ←は連続関数 |
f,g が可測関数ならば, ←は可測関数である。 |
||||||||||
sup fn,inf fn,
|
fn が連続関数であっても, ←は連続関数とはかぎらない。 |
fn が可測関数ならば, ←は可測関数である。 証明は下の余白 |
この表から連続関数と可測関数を分け隔てているものは何かといえば,開集合族とボレル集合体の性質の違いで,集合の可算個の共通部分をとったとき,再び,その集合族に属するといえるか否かです。連続関数の場合は有限個でないとダメなんです。
可測関数の開集合・閉集合に関する性質を挙げておくと,
f を可測な関数とするとき,
(1) R1の任意の開集合 O に対して,f-1(O)∈β
(2) R1の任意の閉集合 F に対して,f-1(F)∈β
(3) R1の任意のボレル集合 B に対して,f-1(B)∈β
(1)でβ⇒O とすれば連続関数の性質となる。
(2)でβ⇒(閉集合全体の集合)とすれば連続関数の性質となる。
工学的な応用でよく目にする普通の集合はほとんど可測空間(可測集合)で,可測でない集合で少しでも”イミのある”空間を考えることの方が難しいです。有名な非可測集合としては「ヴィタリ集合 」がありますが,ここでは詳しく述べませんので,興味のある方はググってみてください。
[1] 「1.ルベーグ流面積」 で考えたディリクレ関数以外の一般的な関数を取り扱うために次のような定義関数(=特性関数),及び単関数を定義します。まず,可測集合を A として,
e(x,A) ≡ 1 ・・・ x ∈A [ 定義関数] 0 ・・・ x A
を導入します。 もし,「A =有理数」 ならば,これはディリクレ関数 [#] と同じです。
[2] 一方,単関数は,区間 [a,b] が共通部分のない有限個の可測集合に,
A =A1∪A2∪・・・・・An
と分割できるとき,実数を, a1,a2・・・・・,an として,
η(x)≡a1e(x,A1)+a2e(x,A2)+・・・・+ane(x,An) [単関数]
と表せるη(x) として定義します。
[3] そして,単関数の重要で自明な性質は,
単関数は可測関数である。
さらに,次のような性質も容易に確かめられます。
η(x),ψ(x)が単関数
⇒ (1) αη(x)+βψ(x)
(2) η(x)ψ(x)
(3) |η(x)|
(4) Max[η(x),ψ(x)],Min[η(x),ψ(x)]
も単関数
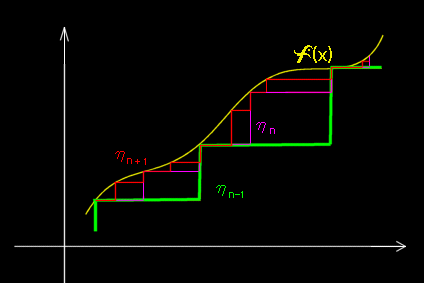
[4] そして,任意の可測関数が単関数(と極限概念)を用いて表せるという事実,すなわち,
|
定理 可測関数 f(x) ( ≧ 0 ) に対して,
となるような単関数の増加列, 0≦η1(x)≦η2(x)≦・・・≦ηk(x)≦・・・ が存在する。 |
言い換えると,可測関数は単関数でいくらでもよく近似できるということです。これは,完備である実数の集合では任意のr∈Rに収束する単調増加する点列を考えることができるという定理の「完備な可測関数バージョン」です。
| ♪ ・・・・ ♪ なぜなの こんなに 幸せなのに 水平線を見ると 哀しくーなる あのころの 自分を遠くで 見ている こーんな感じ ⇒ ・・・・・♪  証明の ルーレット 廻してー アレコレ 深く考えるのは Mystery ・・・・・ |
 |
これでルベーグ積分の厳密な定義に必要な準備は完了です。
・ { fn } が可測関数ならば,sup fnは可測関数の証明
(1) sup fn<∞のとき
任意の実数 b に対して,sup fn(x)<b を満足する x が可測集合であることを言えばよい。
sup fn(x)<b ならば,すべて fn(x)<b であるから
{ x|sup fn(x)< b }=
{ x|fn(x)< b }
右辺の { x|fn(x)< b } は可測集合であり,その可算個の共通部分も可測集合なので,左辺={ x|sup fn(x)< b } も可測集合である。したがって,sup fn(x) は可測関数。
また,inf fn(x) =−sup(-fn(x)) より,inf fn(x) も可測であることが分かる。
(2) sup fn=∞ のとき,
sup fn の値を{+∞}と定めて,拡大実数で考える必要があります。
自然数 N に対して,
{ x|sup fn(x)>N }=![]() { x|fn(x)> N }
{ x|fn(x)> N }
であるが,sup fn=∞ のときは,これがすべての自然数 N について成り立つので,それは,
{ x|sup fn(x)=∞ }= ∞ { x|fn(x)> N }
∩ N=1
と表される。ここで,fn(x)が可測関数なので,右辺は可測関数。
結局(1),(2)合わせて,sup fn(x) は可測関数である。
| ・ { fn } が可測関数ならば, |
|
は可測関数の証明 |
(1) sup fn<∞のとき
これは,gn(x)=sup { fn(x),fn+1(x),・・・ } とおくと,
gn(x) は可測関数
であり,
g1(x)≧・・・≧gn(x)≧gn+1(x)≧ ・・・
であり,単調減少列となり,gn(x)は必ず収束して,
inf gn(x)= gn(x)
上の結果より inf gn(x) は可測関数であるから![]() gn(x)も可測関数。ところが,
gn(x)も可測関数。ところが,
gn(x)= sup { fn(x),fn+1(x),・・・} =limsup fn(x)
である。よって,
limsup fn(x)=
lim fn(x) は可測関数
表記法
{ x|sup fn(x)> a } =
{ x|fn(x)> a }
{ x|inf fn(x)> a } ={ x|fn(x)> a }
{ x|sup fn(x)< b } =
{ x|fn(x)< b }
{ x|inf fn(x)< b } ={ x|fn(x)< b }
sup fn(x) = sup fn(x) n≧1
inf fn(x) = inf fn(x) n≧1
|
fn(x) | = limsup fn(x) = | limsup | fn(x) = | inf | sup | fk(x) | ||||||
| n→∞ | n≧1 | k≧n |
|
fn(x) | = liminf fn(x) = | liminf | fn(x) = | sup | inf | fk(x) | ||||||
| n→∞ | n≧1 | k≧n |
lim Ak= limsup Ak = Ak
lim An = liminf Ak = Ak
An = ∩ An= { x∈X | すべての n∈N について x∈An } n∈N
An = U An= { x∈X | ある n∈N が存在して x∈An } n∈N
| 拡大実数 : |
|
= R ∪ { -∞,∞ } |
±∞ を一つの数のように扱い,次のような規則を定める。
a∈R のとき,−∞<a<∞ と表記する。
a±∞ = ±∞
∞×∞=∞
∞×0=0
著者のメモ
|
Rn の可測集合全体の濃度は, 2 |
である。 | |
| / |
-------------------------------