| 9 グリーンの定理 | |
| f-denshi.com [目次へ] 最終更新日:09/12/04 | |
| サイト検索 | |
グリーンの第1等式,第2等式も参考にしてください。 ⇒[#]
| グリーンの定理 有界な曲面Sの周囲をCとするとき,
が成り立つ。これは次の個別に成り立つ2つの積分の和である。
|
[証明]
 ガウスの定理[#]:
ガウスの定理[#]:
∇・A dV= A・n dS
において,
A=[φ(x,y),−ψ(x,y), 0]
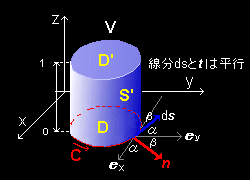
とし,積分範囲は右図のように底面が xy 平面内にある領域 D (この周囲を C
とする)で高さが1の鉛直に立つ柱とします。そしてこの柱の
内部を V
表面を S =D(底面)+D'(上面)+S'(側面)
とすると,ガウスの定理の左辺(体積分)は,
∇・A dV = ∂φ − ∂ψ dxdydz ∂x ∂y
= ∂φ − ∂ψ dxdy・ dz ∂x ∂y
= ∂φ − ∂ψ dxdy ∂x ∂y
一方,ガウスの定理の右辺(面積)は上面と底面に関する積分はキャンセルし合うので,側面S'について考えれば十分です。
このとき,側面では,曲線Cの微分長さをds とすれば,
dS = dzds
とおけるので,側面上の法線単位ベクトルを,n =(cosα,sinα,0)とすれば,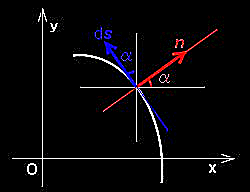
A ・ndS = (φcosα−ψsinα)dzds '
= (φcosα−ψsinα)dzds
= (φcosα−ψsinα)ds
↓cosαds=dy,sinαds=−dx を用いて (ds⊥n )
= (φdy+ψdx)
すなわち,
∂φ − ∂ψ dxdy= (ψdx +φdy) ∂x ∂y
ここで,DをSと改めれば定理を得ます。
[1] グリーンの定理の幾何学的な意味を考えるため,グリーン定理,
∂φ − ∂ψ dxdy = (ψdx+φdy) ∂x ∂y
において,φ(x,y)=x,ψ=(x,y)=0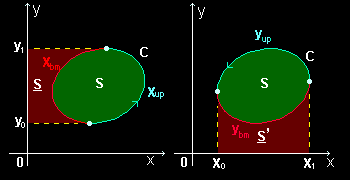 とおくと,
とおくと,
1 dxdy = xdy
今度は,φ(x,y)=0,ψ(x,y)=y とおくと,
1 dxdy =− ydx
この2式の左辺の面積分の範囲はいずれも右図の面積 S にとります。
すると,右辺の線積分はそれぞれ右図を参考にして,
[A] xdy= xupdy+ xbmdy
=(S+S)+(−S)=S
および,
[B] − ydx=− ybmdx− yupdx
=−S'−(−S−S')=S
となります。 結局,閉曲線Cで囲まれた面積Sを求める上記2通りの方法が ”同じだよ” と示していることがわかります。