| Appendix1 2次元のベクトル場 | |
| f-denshi.com [目次へ] 最終更新日:09/12/16 1.と 2.を追加 | |
| サイト検索 | |
[1] 火山地帯であちらこちらの地下からガスが噴出して,地表を這うように流れ出している状況を思い描いてください。この地表のどの地点でどれだけの量のガスがわき出しているかをどのように調べたらよいのでしょうか。必ずしも地下からのガス噴出量を直接計測するために流量計を地表に隙間なく設置する必要はありません。ガスの膨張収縮が無視できる場合は,必要十分な精度で,各地点のガスの流速(流量) A(x,y) がわかれば,各領域 (極限では各点) におけるガスのわき出し量も計算することができるはずです。なぜならば,ある領域に流入したガス量と流出したガス量の差がその領域内でわき出したガス量だからです。以下,ガスの密度がどの場所でも一定であるとの仮定の下で話を進めます。
[2] ガスの各地点での流速A(x,y)=(A1(x,y),A2(x,y))を表した図は,xy平面上の2次元ベクトル場と考えることができます。この平面上で,位置(x,y)を中心に持つ下図に示すような縦Δy,横Δxである,必要なだけ小さな長方形の領域(=囲み)を考えます。その一つの線分1→2に外向きに垂直な法線ベクトルn とその線上の点の流速 A との内積は,その点からを領域の外へ流出するガス量となります。したがって,この内積を辺1→2にわたる線積分,
Φ1-2= 1-2 A ・n ds
がこの線分1→2を通って流出したガスの量Φ1→2を表します。さらに,これを長方形のすべての辺について加算した,
A ・n ds = 1-2 A ・n ds + 2-3 A ・n ds + 3-4 A ・n ds + 4-1 A ・n ds
=Φ1-2+Φ2-3+Φ3-4+Φ4-1
によって計算される量は,この領域の中でわき出したガスの量と考えることができます。そこでベクトル場に対する上記の周回積分を一般的な用語として,わき出し量と呼ぶことにしましょう。
[3] さて,このわき出し量について,囲み1→2→3→4→1に沿って法線ベクトルが,n=(1,0)→(0,1)→(-1,0)→(0,-1)と変ることに注意して,もう少し計算を進めると,
Φ1-2 ≒ Δy/2 A1(x+Δx/2,y+s)ds ≒ Δy/2 A1(x,y)+ ∂A1(x,y) (Δx/2)+ ∂A1(x,y) s ds -Δy/2 -Δy/2 ∂x ∂y
同様に
Φ3-4=− Δy/2 A1(x−Δx/2,y+s)ds ≒− Δy/2 A1(x,y)− ∂A1(x,y) (Δx/2)+ ∂A1(x,y) s ds -Δy/2 −Δy/2 ∂x ∂y
したがって,これらの和は,
Φ1→2+Φ3→4=2 Δy/2 ∂A1(x,y) (Δx/2)ds = ∂A1(x,y) ΔxΔy -Δy/2 ∂x ∂x
同様に
Φ2-3≒ Δx/2 A2(x,y)+ ∂A2(x,y) (Δy/2)+ ∂A2(x,y) s ds -Δx/2 ∂y ∂y
Φ4-1≒−
Δx/2 A2(x,y)− ∂A2(x,y) (Δy/2)+ ∂A2(x,y) s ds -Δx/2 ∂y ∂y
と計算して,その和を求めると,
Φ2-3+Φ4-1≒ ∂A2(x,y) ΔxΔy ∂y
よって,この長方形の領域からのわき出し量は,
A ・n ds ≒ ∂A1(x,y) + ∂A2(x,y) ΔxΔy ∂x ∂y
となります。この積分値が正の値を取るときは文字通りわき出し量でよいのですが,負の値を取るときは,この領域でガスが失われていることを意味するので,吸い込み量と呼ぶ場合もあります。
[4] このような背景を理解した上で,
D(x,y,Δx,Δy)=ΔxΔy ∂A1 + ∂A2 ∂x ∂y
なる量を,0≦Δx≦h,0≦Δy≦h として,極限,
DivA (x,y)≡ D(x,y,Δx,Δy) = ∂A1 + ∂A2 ΔxΔy ∂x ∂y
が存在するとき,これを点(x,y)における2次元の発散と呼びます。
[1]次に,渦 (うず) と呼ばれるものについて考えます。台風,竜巻などが渦を巻いているといいますが,その様子をベクトル解析の言葉で定量的に表してみましょう。発散の定義で考えたときと同じように,平面上の各点でのガスの流速A(x,y)を表した2次元ベクトル場で考えます。その場に有限の物体(紙片など)が置かれたときの様子を思い浮かべてみると,物体がガスの流速方向に流されると同時に回転運動も引き起こされることは日常よく経験することです。この回転は自転であったり,公転であったりしますが,これは物体の境界の接線方向への流速成分に比例して働く力に関係していると考えられます。
流れが不均一だと船は回転しながら流されていく。
[2] そこで,2次元ベクトル場A におかれた小さな長方形の周囲 1→2→3→4→1上の点における流速の接線成分,すなわち,その点の接線ベクトルt と流速Aとの内積A ・t を回転力(=トルク),もしくは,渦の強さに関係付けられる量として定式化します。これが正であれば,正方向 (反時計回り),負であれば負方向(時計回り)への回転に寄与する流れということになります。もちろん,ゼロであれば回転には寄与しません。
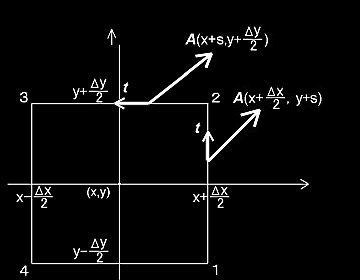
この内積を小片の周囲全体にわたって積算した値
=Γ1→2+Γ2→3+Γ3→4+Γ4→1
A ・t ds = 1→2 A ・t ds + 2→3 A ・t ds + 3→4 A ・t ds + 4→1 A ・t ds
を調べれば,小片全体に及ぼす影響を計算でき,これは小片の重心の周りの回転力と関係付けられる量であって,任意のベクトル場に対するこの周回線積分は循環と呼ばれます。
[3] さて,具体的な計算です。
Γ1→2= Δy/2 A2(x+Δx/2,y+s)ds≒ Δy/2 A2(x,y)+ ∂A2(x,y) (Δx/2)+ ∂A2(x,y) s ds -Δy/2 -Δy/2 ∂x ∂y
Γ3→4=− Δy/2 A2(x−Δx/2,y+s)ds≒− Δy/2 A2(x,y)− ∂A2(x,y) (Δx/2)+ ∂A2(x,y) s ds -Δy/2 -Δy/2 ∂x ∂y
この2つの項の和は,
Γ1→2+Γ3→4=2 Δy/2 ∂A2(x,y) (Δx/2)ds = ∂A2(x,y) ΔxΔy -Δy/2 ∂x ∂x
同様に
Γ2→3≒− Δx/2 A1(x,y)+ ∂A1(x,y) (Δy/2)+ ∂A1(x,y) s ds -Δx/2 ∂y ∂y
Γ4→1≒ Δx/2 A1(x,y)− ∂A1(x,y) (Δy/2)+ ∂A1(x,y) s ds -Δx/2 ∂y ∂y
∴ Γ2→3+Γ4→1=− ∂A1(x,y) ΔxΔy ∂y
と計算を進めることができます。よって,
A ・t ds ≒ ∂A2(x,y) − ∂A1(x,y) ΔxΔy ∂x ∂y
ここで,分散を考えたときと同じように,
R(x,y,Δx,Δy) ≒ ∂A2(x,y) − ∂A1(x,y) ΔxΔy ∂x ∂y
とおき,0≦Δx≦h,0≦Δy≦h として,極限,
RotA (x,y)= R(x,y,Δx,Δy) = ∂A2 − ∂A1 ΔxΔy ∂x ∂y
が存在するとき,これを点(x,y)における2次元の回転,(または渦度)と定義します。
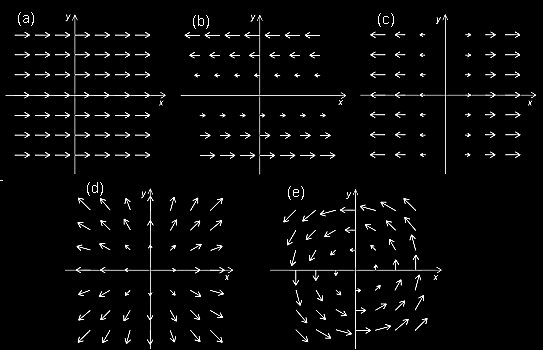
[4] 2次元のベクトル場A (x,y)=(A1,A2) の具体例として,次の5つをあげておきましょう。
| ベクトル場 | (a) | (b) | (c) | (d) | (e) | ||||||||||
| A (x,y)= | (x0,0) | (-y,0) | (x,0) | (x,y) | (-y,x) | ||||||||||
|
0 | 0 | 1 | 2 | 0 | ||||||||||
|
0 | 1 | 0 | 0 | 2 | ||||||||||
| 流線 (c:定数) | y=c | y=c | y=c | y=cx | x2+y2=c | ||||||||||
 |
|||||||||||||||
流線は次の微分方程式の解として定義される曲線群です。
dx = dy A1(x,y) A2(x,y)
全領域で |A|≠0 ならば,一点を通る流線はただ一つ定まります。
|
3次元ベクトル場への拡張:
|
1次元の場合はどうなるでしょうか ?
[0] 物理,工学などへの応用的を考えると,ベクトル場が位置の関数:A (r) として与えられるケースがもっとも一般的です。具体的には,重力やクーロン力などに使われる
F (r)=k ・ r ; k 定数 |r | 3
などがあります。もちろん,これは,線形写像(r ⇒ F (r)) とはなっていません。しかし,ある条件のもとでは局所的に線形写像とみなすことが可能で,
A (r)=Ar +B 0 ; B 0 は定数ベクトル
として取り扱うことができます。ここではその背景について述べます。
[1] C1写像Φ:(u,v) ⇒ (x,y) において十分小さな領域を取り出して考えるならば,初等解析学の教えるところによると,この写像の定義域,値域の微分量は近似的にヤコビ行列を用いた線形写像で,
Δx = xu(u0,A0)) xv(u0,v0) Δu ・ ・ ・ ・ ・[*] Δy yu(u0,A0) yv(u0,v0) Δv
と結び付いていることを思い出しましょう。 復習は ⇒ 実数解析入門 11章[#]
このヤコビ行列を J(Φ)a,b と書くことにします。
[2] ここの「 ベクトル解析 」で使っている記号に改めて,u→x,v→y,および,x→A1,y→A2 と書き直しましょう。
すると,C1写像:(x,y)⇒(A1,A2) および,A =A (A1(r),A2(r))=Φ(r) となり,局所的に成り立つ関係[*] は
ΔA1 =A Δx ΔA2 Δy
または,
ΔA AΔr ⇔ A −A 0 = A(r −r0)
⇔ A =Ar +(A 0−A r0)
となります。ただし,
r = x y
,r0= x0 ,Δr = x−x0 y0 y−y0
,A = A1 A2
,A0= A01 A02
および,A はヤコビ行列[#]で,
A =
∂A1 ∂x x=x0,y=y0
∂A1 ∂y x=x0,y=y0 =
∂A1 ∂x
∂A1 ∂y
≡ A1x A1y A2x A2y
∂A2 ∂x x=x0,y=y0
∂A2 ∂y x=x0,y=y0
∂A2 ∂x
∂A2 ∂y
というのが記号の意味です。 (↑ A2x とは A2 のxに関する偏微分という意味です。)
|
(補足) ちなみに,3変数( x,y,z )から3つのベクトル成分 ( A1,A2,A3) への C1写像を考えるときは,
となります。 |
[3] 結局,C1写像: Φ(r )=A (r)は,局所的には,線形写像
A (r)=Ar +B 0 ; B 0 は定数ベクトル
で近似できます。 ( 記号だけの問題ですが,A0−Ar0 ⇒ B 0 と改めています。)