Appendix　C　円筒座標（円柱座標）
f-denshi.com   ［目次へ］　最終更新日：  21/11/19
サイト検索

１．　円筒座標(円柱座標)　

［１］　デカルト座標と円柱座標の変数変換の式は右図を参考にすれば，

x＝r･cosφ，　　y＝r･sinφ，　　　　z＝z

これを逆に解くと

r＝(x²＋y²)^1/2，　φ＝tan^-1(y/x)，　z＝z　　　　　　　　

ただし，0＜r＜∞，0≦φ＜2π，−∞＜z＜∞ となります。

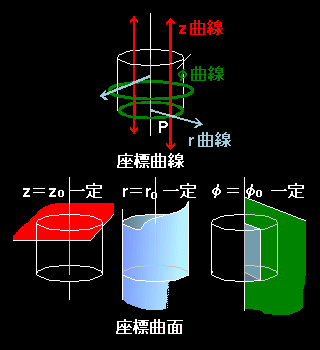［２］　このとき，座標曲線[#]は，

r (r) ＝ (r･cosφ₀，r･sinφ₀， z₀)　 ⇒　r 曲線
r (φ)＝ (r₀･cosφ，r₀･sinφ， z₀)　 ⇒　φ曲線
r (z) ＝ (r₀･cosφ₀，r₀･sinφ₀，z)　 ⇒　z 曲線

また，座標曲面[#]は定義より

r₀＝(x²＋y²)^1/2　    ⇒　r 曲面
φ₀＝tan^-1(y/x) 　   ⇒　φ曲面
z₀＝z　　 　　　 　 　⇒　z 曲面

となります。各曲面，曲線の幾何学的な形状は右図を参照して下さい。また，空間のどの点についてもその点を通る r，φ，z 各座標曲面と各座標曲線が一つずつ存在することも確かめられますね。

［３］　計量係数[#]は，↓r ＝(x,y,z)＝(r･cosφ，r･sinφ，z)なので，

∂r	＝(cosφ，sinφ，0)，	∂r	＝(−r sinφ，r cosφ，0)，	∂r	＝(0，0，1)
∂r		∂φ		∂z

より，
　　　　　h_r ＝(cos²φ＋sin²φ)^1/2　　　    　＝1
　　　　　h_φ＝{(−r sinφ)²＋(r cosφ)²}^1/2 ＝r
　　　　　h_z　　　　　　　　　　　　　　　　　　　　＝1　　　　　　

したがって，デカルト座標，円柱座標の基底ベクトルの関係は

e_r　＝　cosφe_x＋sinφe_y
e_φ ＝−sinφe_x＋cosφe_y
e_z　＝　e_z

e_x＝cosφe_r−sinφe_φ　　　←以前間違って，φがθとなっていました。
e_y＝sinφe_r＋cosφe_φ
e_z＝　e_z　　　

となります[#]。また，e_r，e_φ，e_zが互いに直交していることも簡単に確かめられます。

微分要素[#]： dr ＝dre_r＋rdφe_φ＋dze_z
体積要素[#]： dＶ＝dxdydz＝r dr dφdz　

［４］　以下，結果だけ書きます。
勾配(円筒座標)

gradψ＝		∂ψ	er＋	∂ψ	eφ＋	∂ψ	ez
		∂r		r∂φ		∂z

発散(円筒座標)

divA ＝	1		∂(rAr)	＋	∂(Aφ)	＋	∂(rAz)
	r		∂r		∂φ		∂z

＝	∂(rAr)	＋	∂Aφ	＋	∂Az
	r∂r		r∂φ		∂z

回転(円筒座標)

rotA ＝

∂(1･Az)

−

∂(r･Aφ)

er＋

∂(1･Ar)

−

∂(1･Az)

eφ＋

∂(r･Aφ)

−

∂(1･Ar)

ez

r∂φ

r∂z

∂z

∂r

r∂r

r∂φ

＝

∂Az

−

∂Aφ

er＋

∂Ar

−

∂Az

eφ＋

∂(r･Aφ)

−

∂Ar

ez

r∂φ

∂z

∂z

∂r

r∂r

r∂φ

ラプラシアン(円筒座標)

div･gradψ＝

1

∂

r･

∂ψ

＋

∂

1

･

∂ψ

＋

∂

r･

∂ψ

r

∂r

∂r

∂φ

r

∂φ

∂z

∂z

＝	∂2ψ	＋	1	･	∂ψ	＋	1	･	∂2ψ	＋	∂2ψ
	∂r2		r		∂r		r2		∂φ2		∂z2

SUSTAINABLE　TOKIWADAIGAK　SINCE　2002

２．具体例

円筒座標の応用１：　無限直線電流がつくる磁場[#]の計算

ビオ-サバールの法則の積分形[#]

H ＝	I		ds ×(r−s)	････　[*]
	4π		|r−s|3

を用いて計算します。

デカルト座標系で，z軸正方向へ電流 I が流れていると想定して，各ベクトルを，

ds＝(0，0，ds)　　　　　　＝0･e_x＋0･e_y＋dse_z　　　　　　　　　･･･　(1)
s＝(0，0，s)　　　　　　　　＝0･e_x＋0･e_y＋se_z
r＝(Rcosφ，Rsinφ，Z)　＝Rcosφe_x＋Rsinφe_y＋Ze_z

∴　r -s＝Rcosφe_x＋Rsinφe_y＋(Z−s)e_z　　　　　　　　　･･･　(2)

とおくことにします。円筒座標系に変換するめに，[３]の基底変換の式，

e_x＝cosφe_r−sinφe_φ
e_y＝sinφe_r＋cosφe_φ
e_z＝　e_z　　　

を(1)，(2)式に代入して，

　ds ＝dse_z　　
　　　＝( 0，0，ds )
r -s＝Rcosφ(cosφe_r−sinφe_φ)＋Rsinφ(sinφe_r＋cosφe_φ)＋(Z−s)e_z
　　　＝Re_r＋(Z−s)e_z
　　　＝(R，0，Z-s)　　　　　[円筒座標系： R，φ，z成分の順に並べて]

すると，円筒座標系での ds と (r−s) との外積は，

ds ×(r−s)＝		er	eφ	ez
		0	0	ds
		R	0	Z−s

＝Rdse_φ＝( 0，Rds，0 )　　　　[ r，φ，z成分の順に並べたベクトルの円筒座標表示]

のように計算されます。(円筒座標系も直交座標系の一つなので，デカルト座標系と同様な外積の成分計算が許される。)　一方，[*]式の被積分関数の分母は，

|r−s|³　＝｛(Rcosφ)²＋(Rsinφ)²＋(Z-s)²｝^3/2　＝｛R²＋(s−Z)²｝^3/2　　　　

これはスカラー量なので，座標系の取り方には関係しません。結局，円筒座標系では，

ds ×(r−s)	＝	Rds	eφ＝			0，	Rds	，0
|r−s|3		｛R2＋(s−Z)2｝3/2					｛R2＋(s−Z)2｝3/2

となります。したがって，磁場も円筒座標系のφ成分のみで，

H ＝

I

Rds

･eφ

＝

0，

I

Rds

，０

4π

｛R2＋(s−Z)2｝3/2

4π

｛R2＋(s−Z)2｝3/2

↓　変数変換　u＝s-Z，および，uに関する偶関数であることから，

＝	2I		R2du	･eφ
	4πR		｛R2＋u2｝3/2

＝	I		u		∞	･eφ
	2πR		R2＋u2		0

＝	I	･eφ
	2πR

と計算されます。

円筒座標の応用２：円電流が遠方に作る磁場

円電流(半径=a)が，十分遠方の位置r (a<<|r |＝(R²＋Z²)^1/2　に形成する静磁場の計算

デカルト座標系で，z軸右ねじ方向へ電流 I が流れていると想定して，各ベクトルを，

ds＝-asinθdθ･e_x＋acosθdθ･e_y＋0･e_z　･･･　(1)
s＝acosθ･e_x＋asinθ･e_y＋0･e_z
r＝Rcosφe_x＋Rsinφe_y＋Ze_z

∴　r -s＝(Rcosφ-acosθ)e_x＋(Rsinφ-asinθ)e_y＋Ze_z　･･･　(2)

とおくことにします。円筒座標系に変換するめに，[３]の基底変換の式，

e_x＝cosφe_R−sinφe_φ
e_y＝sinφe_R＋cosφe_φ
e_z＝　e_Z　　　

を(1)，(2)式に代入して，

　ds ＝-asinθdθ(cosφe_R−sinφe_φ)＋acosθdθ(sinφe_R＋cosφe_φ)＋0･e_Z
　　　＝ a(cosθsinφ-sinθcosφ)dθe_R＋a(sinθsinφ＋acosθcosφ)dθe_φ
　　　＝asin(φ-θ)dθe_R＋acos(φ-θ)dθe_φ

r -s＝(Rcosφ-acosθ)(cosφe_R−sinφe_φ)＋(Rsinφ-asinθ)(sinφe_R＋cosφe_φ)＋Ze_Z
　　　＝(R-acosθcosφ-asinθsinφ)e_R＋(acosθsinφ-asinθcosφ)e_φ＋Ze_Z
　　　＝(R-acos(φ-θ))e_R＋asin(φ-θ)e_φ＋Ze_Z

すると，円筒座標系での ds と (r−s) との外積は，

ds ×(r−s)＝dθ		eR	eφ	eZ
		asin(φ-θ)	acos(φ-θ)	0
		R-acos(φ-θ)	asin(φ-θ)	Z

＝aZcos(φ-θ)dθe_R−aZsin(φ-θ)dθe_φ＋(a²-aRcos(φ-θ))e_Z

一方，a<<|r |＝(R²＋Z²)^1/2　と近似可能なとき，

1	＝｛(R-acos(φ-θ))2＋(asin(φ-θ))2＋Z2｝-3/2
|r−s|3

　　　　　　　　＝｛R²＋Z²−2aRcos(φ-θ)＋a²｝^-3/2

　　　　　　↓　a²/(R²＋Z²)の項を落として

≒(R2＋Z2)-3/2			1−	2aR	cos(φ-θ)		-3/2
				R2＋Z2

　　　　　　　↓　(1＋ε)^m≒1＋mε

≒(R2＋Z2)-3/2			1＋	3aR	cos(φ-θ)
				R2＋Z2

したがって，ビオ-サバールの法則から円筒座標で表した磁場は，

e_R成分

HR＝	I		aZcos(φ-θ)(R2＋Z2)-3/2			1＋	3aR	cos(φ-θ)		dθ
	4π						R2＋Z2

＝	I				3a2ZR	cos2(φ-θ)		dθ
	4π				(R2＋Z2)5/2

e_φ成分

Hφ＝−	I		aZsin(φ-θ)(R2＋Z2)-3/2			1＋	3aR	cos(φ-θ)		dθ
	4π						R2＋Z2

　　＝0

e_Z成分

HZ＝	I		(a2-aRcos(φ-θ))(R2＋Z2)-3/2			1＋	3aR	cos(φ-θ)		dθ
	4π						R2＋Z2

↓		cos(φ-θ)dθ＝0　に注意して，

＝	I		(R2＋Z2)-3/2			a2−	3a2R2	cos2(φ-θ)		dθ
	4π						R2＋Z2

＝	I	(R2＋Z2)-3/2			2πa2−	3a2R2	π
	4π					R2＋Z2

＝	Ia2		2−	3R2
	4(R2＋Z2)3/2			R2＋Z2

一方，円筒座標と球座標との対応は，r とz軸とのなす角度をθとして，

r cosθ＝Z
r sinθ＝R
R²+Z²＝r²

の対応があります。そこで，円筒座標を，

HR＝	3Ia2ZR	＝	3Ia2r2cosθsinθ	＝	3Ia2cosθsinθ
	4(R2＋Z2)5/2		4(r2)5/2		4r3

HZ＝	Ia2		2−	3R2		＝	Ia2		2−3sin2θ
	4(R2＋Z2)3/2			R2＋Z2			4r3

と書いておきます。すると，球座標で表した磁場(H_r，H_φ，H_θ)は，　　(R-Z面内でφ軸周りにθ回転させせればよい)

Hθ＝HRcosθ−HZsinθ＝		Ia2sinθ
		4r3

Hr＝HRsinθ＋HZcosθ＝		Ia2cosθ
		2r3

H_φ＝0

もちろん，円筒座標系を介さずに，デカルト座標から直接，球座標を計算することもできます。(演習問題：答えはPDF版ベクトル解析で)

まとめです

円電流がつくる磁場 円筒座標 球座標 HR＝ 3Ia2ZR 4(R2＋Z2)5/2 Hφ＝0 HZ＝ Ia2 2− 3R2 4(R2＋Z2)3/2 R2＋Z2 Hθ＝ Ia2sinθ 4r3 Hφ＝0 Hr＝ Ia2cosθ 2r3

［目次へ］