 |
4 測地線 |
|
| f-denshi.com 最終更新日: 校正中 |
| サイト検索 |
|
1.測地線の微分方程式
曲面上の2点を結ぶ曲線の中でその長さが最小の曲線は,その2点間の測地線と呼ばれます。また,測地線上ではどの点でも測地曲率が 0 (ゼロ) となっています。以下,このことを,「測地線の微分方程式」を求めることで確認してみましょう。
[1] 曲面p (u,v)上の曲線を p (t)=p (u1(t),u2(t) ) と書くこととします。ここでは,t は弧長パラメータとして途中の計算を進めますが,最終結果は一般のパラメータの場合と同じとなることが示されます。
|
dp |
= |
∂p |
|
du1 |
+ |
∂p |
|
du2 |
|
|
|
|
|
| dt |
du1 |
dt |
du2 |
dt |
 |
dp |
 |
2 |
=g11 |
du1 |
|
du1 |
+2g12 |
du1 |
|
du2 |
+g22 |
du2 |
|
du2 |
|
|
|
|
|
|
|
|
| dt |
|
dt |
dt |
dt |
dt |
dt |
dt |
となりますが,曲線の2点 p (t1),p (t2) 間の長さは,
|
|
|
|
|
|
|
|
| S= |
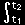 |
|
dt= |
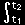 |
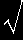 |
 |
gjk |
duj |
|
duk |
|
|
| dt |
dt |
|
dt |
で求められます。今,u1(t),u2(t) はp (t1)とp (t2)とを結ぶ最短の経路を与える関数であるとします。
[2] ここで,変分法を適用するために経路 (曲線の形) がここからわずかに変化した次のようなp~(t) を考えます。
p ~(t)=(u~1(t),u~2(t))
ただし,λを実数パラメータとして,
u~1(t)≡u1(t)+λw1(t)
u~2(t)≡u2(t)+λw2(t)
であるものとします。これは元の最短曲線にλwi(t) が肉付け付けされた曲線を表しますが,曲線の両端では,
w1(t1)=w1(t2)=w2(t1)=w2(t2)=0 [両固定端条件] [#]
をみたすという条件が付きます。
次に,
|
|
|
|
|
|
|
|
|
| S~(λ)= |
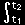 |
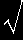 |
 |
gjk |
du~j |
|
du~k |
|
|
| dt |
dt |
|
dt |
= |
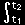 |
|
|
 |
F(t,λ) |
|
dt |
| F(t,λ) = |
 |
gjk |
du~j |
|
du~k |
|
|
| dt |
dt |
|
とおきます。ここで,t が弧長パラメータとすれば,
|
|
|
|
|
|
|
|
= |
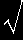 |
 |
gjk |
duj |
|
duk |
|
|
| dt |
dt |
|
=1 |
⇔ F(t,0)=1 |
を満たすことを確認しておきましょう。
[3] さて,S~(λ) がλ=0 において極値条件(最小値をとるときの必要条件)
を満たすです。 計算を実行すると,
|
d |
S~(0)= |
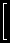 |
d |
|
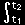 |
|
|
|
 |
F(t,λ) |
dt |
|
 |
|
|
|
|
| dλ |
dλ |
λ=0 |
| = |
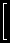 |
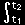 |
1 |
|
dF(t,λ) |
|
dt |
 |
|
|
|
|
|
|
|
|
| 2 |
 |
F(t,λ) |
|
|
dλ |
λ=0 |
| = |
|
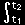 |
1 |
・ |
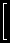 |
| dF(t,λ) |
 |
λ=0 |
dt |
|
| dλ |
|
|
| [F(t,λ)]λ=0 |
|
|
|
|
| ↓ |
 |
F(t,0) |
= 1 & F をλで微分 |
| = |
1 |
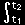 |
 |
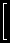 |
 |
 |
d |
|
| dλ |
|
gjk |
 |
du~j |
|
du~k |
|
|
| dt |
dt |
|
 |
λ=0 |
+ |
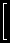 |
|
 |
| gjk |
 |
|
du~j |
 |
du~k |
|
|
| dt |
dt |
|
+ |
 |
| gjk |
du~j |
 |
d |
|
| dλ |
|
du~k |
 |
|
|
| dt |
dt |
|
 |
λ=0 |
 |
dt |
|
| 2 |
↑ 第2,3項は j,k に対して対称的なのでまとめる
| = |
1 |
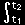 |
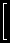 |
|
 |
|
|
 |
λ=0 |
duj |
|
duk |
|
|
| dt |
dt |
|
dt + |
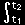 |
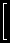 |
 |
| gjk |
|
|
du~j |
 |
λ=0 |
duk |
|
|
| dt |
dt |
|
|
dt |
|
| 2 |
| = |
1 |
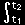 |
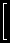 |
|
 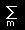 |
|
|
 |
λ=0 |
duj |
|
duk |
|
|
| dt |
dt |
|
dt + |
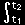 |
 |
|
|
dt |
|
| 2 |
| = |
1 |
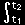 |
 |
|
 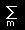 |
|
dt + |
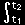 |
 |
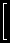 |
wj(t)gjk |
|
duk |
|
| dt |
|
 |
|
t=t2 |
− |
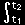 |
 |
| wj(t) |
d |
 |
gjk |
|
duk |
|
|
| dt |
dt |
|
 |
dt |
|
|
| 2 |
t=t1 |
↓wj(t1)=wj(t2)=0 & 第3項の添字 j を mと書き換え
| = |
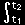 |
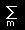 |
 |
1 |
 |
|
− |
|
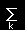 |
|
d |
 |
gmk |
|
duk |
|
|
| dt |
dt |
|
 |
 |
wm(t) dt |
|
| 2 |
[4] この積分が任意の wm(t) に対して 0 となるためには,
でなければならないことが分かります。
この式をもっと見通しのよい式にするために,まず,第1項の微分を実行すると,
|
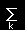 |
|
|
+ |
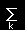 |
|
|
|
|
|
| = |
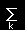 |
|
|
+ |
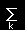 |
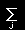 |
∂gmk |
|
duj |
|
duk |
|
|
|
| ∂uj |
dt |
dt |
|
|
|
|
|
| = |
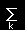 |
|
|
+ |
1 |
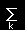 |
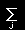 |
  |
∂gmk |
+ |
∂gmj |
 |
|
duj |
|
|
duk |
|
|
|
|
| ∂uj |
∂uk |
dt |
dt |
|
|
|
|
| 2 |
したがって,第1項と第2項合わせて,
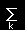 |
|
|
+ |
1 |
|
 |
  |
∂gmk |
+ |
∂gmj |
− |
∂gjk |
|
 |
|
duj |
|
|
duk |
|
|
|
|
|
|
| ∂uj |
∂uk |
∂um |
|
dt |
dt |
|
 |
=0 |
|
| 2 |
となります。
[5] さらに,この式に gim をかけて,m について和をとれば,
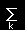 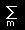 |
|
|
+ |
1 |
|
 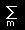 |
gim |
 |
∂gmk |
+ |
∂gmj |
− |
∂gjk |
|
 |
|
duj |
|
|
duk |
|
|
|
|
|
|
| ∂uj |
∂uk |
∂um |
|
dt |
dt |
|
|
=0 |
|
| 2 |
↓ 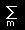 gimgmk=δki
gimgmk=δki
|
|
|
+ |
1 |
|
 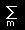 |
gim |
 |
∂gmk |
+ |
∂gmj |
− |
∂gjk |
|
 |
|
duj |
|
|
duk |
|
|
|
|
|
|
| ∂uj |
∂uk |
∂um |
|
dt |
dt |
|
|
=0 |
|
| 2 |
ここで,
| Γijk = |
1 |
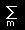 |
gim |
 |
∂gmk |
+ |
∂gmj |
− |
∂gjk |
|
 |
|
|
|
|
|
| 2 |
∂uj |
∂uk |
∂um |
|
であること [#] を用いれば,
測地線の微分方程式
| d2ui |
+ |
 |
Γijk |
duj |
|
duk |
=0 |
|
|
|
| dt2 |
dt |
dt |
|
これが,曲面上の2点を最短距離で結ぶ曲線が満たさなければならない測地線の微分方程式と呼ばれるものです。
2.測地曲率ベクトル
[1] 引き続き曲面内にある曲線の曲率を考えていきます。以下のことは任意の曲面内にある任意の曲線について当てはまることですが,イメージしやすいように球面内に描かれた円を考えましょう。
下図を見てください。地球上の緯線は,赤道を除けば,地球の中心を通らない円 (=小円) となリます。したがって,その緯線上の P点における曲率ベクトル [#] は,その点からその小円の中心 Op を向くベクトルとなっています。
また,この曲率ベクトルは,Pにおける接平面に垂直なベクトルと接平面内にある経線方向のベクトルとの2つのベクトルの和に分解して表すことができます。
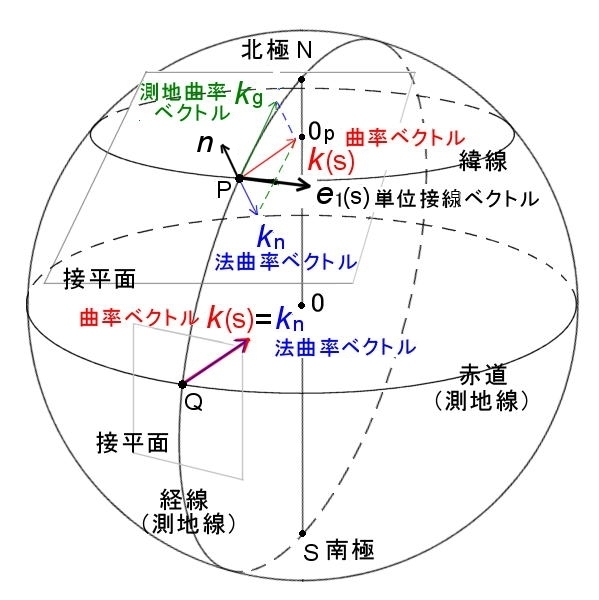 |
図1.5
球面を地球儀に見立て,各種曲線とそれを特徴づけるベクトルを図示しています。 |
[2] これは球面だけに限ったことではなく,任意の曲面上の任意の曲線 p (s) について,曲線の曲率ベクトル k(s)=p ''(s) (曲線に接する小円の中心方向を示す) は,接平面内のベクトル kg と接平面に垂直なベクトルkn とに分解して,
k(s) = kg+kn (厳密な数式は後ほど示します。)
と一意的に書くことができ, (図1.5 をみてください。)
kg : 測地曲率ベクトル
kn : 法曲率ベクトル (球の中心方向を示す)
と呼びます。さらに,その大きさを,
定義
|kg|=κg(s) = | k(s)・(n×e1(s)) | : 測地曲率
|kn|=κn(s) = | (k(s)・n | : 法曲率 kn=κnn
|
と定義します。e1(s)は曲線の単位接線ベクトル[#],n ≡ np (u,v) は接平面の単位法線ベクトル[#] ,n×e1(s) は接平面内のkgと同方向を向く単位ベクトルです。
[3] また,曲面内の曲線の曲線の曲率は,
| κ=|k(s)|= |
|
|
|
 |
κn2+κg2 |
≧|κn| |
を満たしています。等式が成り立つκg=0 とき,すなわち,
「 曲線の曲率ベクトルと曲面の法曲率ベクトルが一致する 」
( ↑ 測地線の別の定義の一つ )
ような状況下であるとき,もっとも曲線曲がり方が小さくなりますが,法曲率κn だけは曲がっていることを示しています。
球面の場合であれば,球面上の曲線で最も曲がりの少ない曲線は,経線や赤道のような大円(の一部)ですが,これは球面上の2
点を最短距離で繋ぐ最も曲がり方の少ない曲線群ということになります。
[4] 最後に,測地曲率κg≡ 0 を満たす点からなるもっとも曲がり方の小さい曲線が測地線の微分方程式を満たしていること,曲率ベクトルは測地曲率ベクトルと法曲率ベクトルとの和で表せることを示しておきましょう,
|
dp |
= |
∂p |
|
du |
+ |
∂p |
|
dv |
= |
du |
pu+ |
dv |
pv |
|
|
|
|
|
|
|
|
| ds |
du |
ds |
dv |
ds |
ds |
ds |
| = |
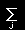 |
|
duj |
p j |
|
| ds |
を用いて曲率ベクトルを計算すると,
| k (s)= |
d2p |
= |
|
d |
|
dp |
|
|
|
|
| ds2 |
ds |
ds |
| = |
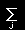 |
d2uj |
p j + |
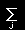 |
duj |
|
|
 |
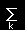 |
p jk |
|
duk |
|
 |
|
|
|
| ds2 |
ds |
ds |
↓ ガウスの公式 (2.213)
| = |
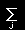 |
d2uj |
p j + |
 |
duj |
|
duk |
 |
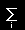 |
Γijkpi+hjkn |
 |
|
|
|
|
| ds2 |
ds |
ds |
| = |
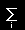 |
 |
d2ui |
+ |
 |
Γijk |
duj |
|
duk |
 |
pi |
+ |
 |
hjk |
 |
duj |
|
duk |
 |
n |
|
|
|
|
|
|
| ds2 |
ds |
ds |
ds |
ds |
|
|
|
|
|
|
kg |
|
kn |
すなわち,第1項は測地曲率ベクトルkg,第2項は法曲率ベクトルkn を与えています。特に第1項が 0 となる条件式は,1.で求めた式と同一であり,測地線の微分方程式となっています。
曲面上の測地線の微分方程式を具体的な形を示しておきます。
|
【定理5 】 測地線の微分方程式
曲面上の曲線 p(u, v) = (u(s), v(s)) が測地線であるための必要十分条件は,u(s), v(s) が次の微分方程式を満たすことである。
|
|
d2u |
|
+Γuuu |
|
du |
|
du |
|
+2Γuuv |
|
du |
|
dv |
|
+Γuvv |
|
dv |
|
dv |
|
=0 |
|
|
|
|
|
|
|
|
| ds2 |
ds |
ds |
ds |
ds |
ds |
ds |
|
|
d2v |
|
+Γvuu |
|
du |
|
du |
|
+2Γvuv |
|
du |
|
dv |
|
+Γvvv |
|
dv |
|
dv |
|
=0 |
|
|
|
|
|
|
|
|
| ds2 |
ds |
ds |
ds |
ds |
ds |
ds |
|
[目次へ]
SUSTAINABLE TOKIWADAIGAK SINCE 2002
![]() gimgmk=δki
gimgmk=δki