| 1 PL多様体の定義 | ||
| f-denshi.com [目次へ] 最終更新日:23/07/17 校正中 | ||
| サイト検索 | ||
PL多様体のPLとは,piecewise linear (区分的に線形) の頭文字をとったものです。前ページまでの多様体は微分可能な角のない滑らかな図形をイメージした議論でしたが,このページからは多面体のような微分できない角のある図形のトポロジーについて解説していきます。
[1]
R3 における直線,平面 などを拡張して,n次元ユークリッド空間 Rn 上の直線,平面 などについて定義します。
以下,ことわりなく,
点 pk=(x1,x2,・・・,xn)
実数 ak,ck,sk,tk ( k=1,2,…,r ; r≦n )
とします。
基本的な図形の表した方です。
2点通る直線
p0p1={t0p0+t1p1|t0+t1=1}
線分 (1単体)
|p0p1|={t0p0+t1p1|t0+t1=1,t0≧0,t1≧0}
R3 の中であれば高校生レベルの話ですが,ここでは,p0,p1は n次元ユークリッド空間の点と考えます。
[2]
3点通る平面
p0p1p2 ={t0p0+t1p1+t2p2|t0+t1+t2=1}
三角形 (2単体)
|p0p1p2|={t0p0+t1p1+t2p2|t0+t1+t2=1,t0≧0,t1≧0,t2≧0}
ただし,3点 p0,p1,p2 は同一直線上にあってはいけません。 その条件は,
この条件を満たすとき p0,p1,p2 は一般の位置にあるといいます。
ここ条件は言い換えると,
ベクトル(p1−p0),(p2−p0)が1次独立
⇔ c1(p1−p0)+c2(p2−p0)=0 ⇒ c1=c2=0
⇔ (c1+c2)p0−c1p1−c2p2=0 ⇒ c1=c2=0
⇔ a0p0+a1p1+a2p2=0, a0+a1+a2=0 ⇒ a0=a1=a2=0
4点通る3次元空間
p0p1p2p3 ={ t0p0+t1p1+t2p2+t3p3|t0+t1+t2+t3=1 }
四面体 (3単体)
|p0p1p2p3|={ t0p0+t1p1+t2p2+t3p3|t0+t1+t2+t3=1,t0≧0,t1≧0,t2≧0,t3≧0 }
ただし,4点は同一平面上にあってはいけません。その条件は,平面のときと同様に考えて,
この条件をみたすとき,p0,p1,p2,p3は一般の位置にあるといいます。
[4]
さらに,n次元ユークリッド空間の5点以上の点を通る図形を考えることもできます。
|
定義 一般の位置 Rn の異なる点 p0,p1,…,pm と実数 a0,a1,…,am に対して, a0p0+a1p1+…+ampm=0, a0+a1+…+am=0 ならば, a0=a1=…=am=0 であるとき, 点 p0,p1,…,pm は一般の位置にある。 という。 |
この用語を用いて,
|
定義 m次元単体 Rn の点 p0,p1,…,pm ,(m≦n) が一般の位置にあるとき, p0p1…pm ={ t0p0+t1p1+…+tmpm|t0+t1+…+tm=1 } を m+1 点 p0,p1,…,pm を通るm次元空間という。 また, |p0p1…pm|={ t0p0+t1p1+…+tmpm| をm次元単体,または,m単体という。 さらに,
をm単体の重心, (t0,t1,…,tm)をm次元空間の重心座標という。
|
m単体σの次元が m であることを明示したいときは,σm と表します。
例
点 0次元単体 (0単体) σ0=|p0|
線分 1次元単体 (1単体) σ1=|p0p1|
三角形 2次元単体 (2単体) σ2=|p0p1p2|
四面体 3次元単体 (3単体) σ3=|p0p1p2p3|
↑中身のある
|
定義 r 辺単体 m単体が与えられたとき,m+1個の点から r+1 個 (0≦r≦m) 選び出して作られる単体をm単体の r 辺単体 という。 m単体σmの r辺単体がτr であることを,τr<σm,または,τ<σと表す。 |
0辺単体を頂点,1辺単体を辺,2辺単体を面,3単体を体ということもあります。
例
3単体の3辺単体は,|p0p1p2p3| (3単体自身)
3単体の2辺単体は,|p1p2p3|,|p0p2p3|,|p0p1p3|,|p0p1p2|
3単体の1辺単体は,|p0p1|,|p0p2|,|p0p3|,|p1p2|,|p1p3|,|p2p3|
3単体の0辺単体は,|p0|,|p1|,|p2|,|p3|
定義から容易に分かるように,m単体の r辺単体の個数は,
m+1Cr+1= (m+1)! (r+1)!(m−r)!
で与えられます。
[1]
|
定義 複体 (単体的複体) 複体 (単体的複体) とは,単体の集合 K であって, (1) σ∈K,τ<σ ⇒ τ∈K [辺単体をすべて含む] (2) σ,τ∈K,σ∩τ≠φ ⇒ σ∩τ<σ かつ σ∩τ<τ を満たすこととする。 特に,単体σのすべての辺単体からなる集合は複体となり,K(σ) と書く。 |
例
σ=|p0p1p2|ならば,
K(σ)={|p0p1p2|,|p1p2|,|p0p2|,|p0p1|,|p0|,|p1|,|p2| }
となる。
例
下図は,K(σ3) U K(τ2) U K(υ) からなる一つの単体複体 K
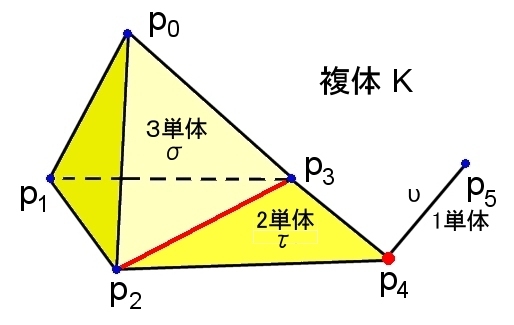
K={ |p0p1p2p3|,
|p1p2p3|,|p0p2p3|,|p0p1p3|,|p0p1p2|,|p2p3p4|,
|p0p1|,|p0p2|,|p0p3|,|p1p2|,|p1p3|,|p2p3|,|p2p4|,|p3p4|,|p4p5|,
|p0|,|p1|,|p2|,|p3|,|p4|,|p5| }
特に,
σ3 ∩τ2=|p2p3| < σ3 ,τ2
τ2∩υ=|p4| < τ2,υ
が成り立っていることに注意。
例 複体ではない例
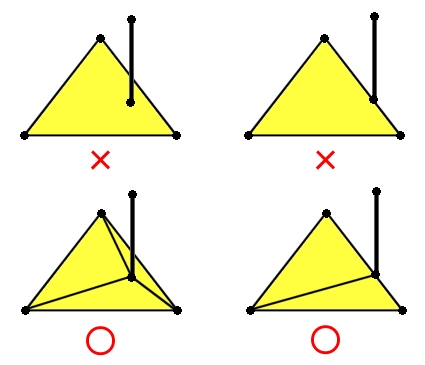
上段は複体ではないが,
下段のように三角形(2単体)を組み合わせて考えれば複体である。
部分複体
複体Kの部分集合が複体となるとき,その部分集合を,Kの部分複体という。
特に,複体K(σ)からσを除いた,
K(∂σ)=K(σ)−{σ}
は K(σ)の部分複体となる。
例
σ= |p0p1p2p3| (3単体) ならば,
K(∂σ)={ |p1p2p3|,|p0p2p3|,|p0p1p3|,|p0p1p2|,
|p0p1|,|p0p2|,|p0p3|,|p1p2|,|p1p3|,|p2p3|,
|p0|,|p1|,|p2|,|p3| }
となり,四面体の表面部分からなる複体となっている。
[3]
|
定義 複体K に属する単体の最大次元の値を複体Kの次元といい,dim K と書く。 複体K に属する r次元以下の単体すべてからなる集合を r骨格といい K(r) と書く。 |
特に,dimK=m ならば,
K(m)=K,
σがm単体であれば,
K(σ)(m-1)=K(∂σ)
が成り立っている。
例

上の複体K であれば, dimK=3
1骨格は,K(1)={ |p0p1|,|p0p2|,|p0p3|,|p1p2|,|p1p3|,|p2p3|,|p2p4|,|p3p4|,|p4p5|,
|p0|,|p1|,|p2|,|p3|,|p4|,|p5| }
[4]
有限複体・無限複体
有限個の単体から構成される複体を有限複体という。有限複体でない複体を無限複体という。
[5]
|
定義 多面体 複体 K に属するすべての単体の和集合からつくられる図形を K の多面体といい,|K| と表す。 |
逆に多面体を単体の集合に分割して,対応する複体を作ることもできます。そして,任意の多面体 X に対して,ある単体的複体 K が存在して,X=|K|と表せることが示されます。 そのような単体的複体 K を多面体 X の 単体分割 といいます。詳しくは,後ほど ”胞体の細分” のところで再び議論します。
例
特に単体 σ=|p0p1p2| ならば,
| K(σ) | = σ= |p0p1p2|
である。
[6]
多面体 |K(∂σ)| をσの境界といい,∂σと表す。
多面体 |K(σm)| =σm は Dm と位相同型であるが,図形 |K(∂σm)|=∂σm は Sm-1と位相同型である。
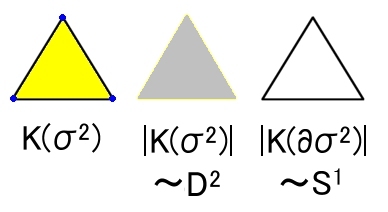 |
| 上図は m=2 の場合の複体 K と多面体 |K| 〜D2と境界 |∂K|〜S1 。 |
|K(σm)|から |K(∂σm)|の除いた部分は内部といい,Int(|K(σm)|)=Intσm と表しますが,厳密な定義は後ほど胞体の説明 [#] のところで示します。
[7]
Rn の図形 X に対して,
X上の任意の点 x と X上にない点 p0 を両端とする線分 |p0x| が x 以外の点で交わらないとき,p0 と X は錐構成可能な位置にある。
という。p0 と X が錐構成可能な位置にあるとき,線分 | p0x | 全体の集合,
p0 *X ≡ U | p0x| x∈X
を 「 p0 を頂点,X を底とする錐 」 という。
特に上記の図形 X が複体 K からできる多面体 | K | であるとき,錐複体を次のように定義する。
|
定義 錐複体 p0 *K ≡ K ∪{ p0*σ|σ∈K } ∪ { |p0| } ここで,σが Kの m単体であれば,p0 *σ は m+1単体である。 |
例
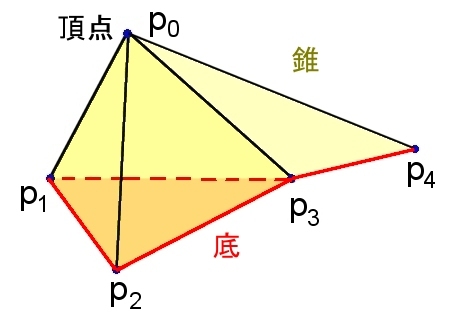
頂点 {|p0|}
複体 K={ |p1p2p3|,|p1p2|,|p1p3|,|p2p3|,|p3p4|,|p1|,|p2|,|p3|,|p4| }
底 |p1p2p3| U |p3p4|
錐複体 p0 *K
≡ K ∪{ |p0p1p2p3|,|p0p1p2|,|p0p1p3|,|p0p2p3|,|p0p3p4|,|p0p1|,|p0p2|,|p0p3|,|p0p4| } ∪ { |p0| }
[8]
|
定義 複体 K,L の多面体が|K|=|L|であり,任意の単体τ∈Lに対して K の単体σが存在して,τ⊂σであるとき,L
を K の細分という。 |
このとき,任意のτに対して,Intτ⊂Intσ となるσはただ一つ定まる。
例
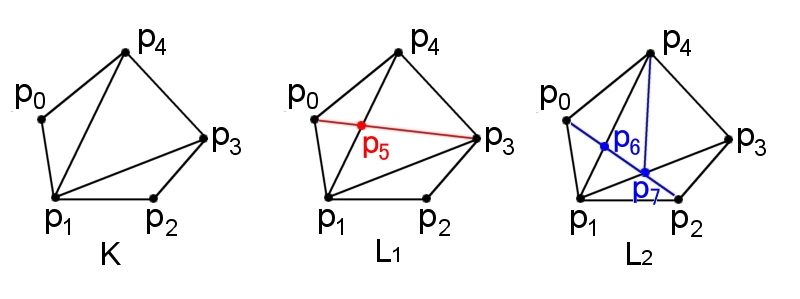
L1,および,L2 はどちらも K の細分となっている。
L1について,
Int |p1p5| ⊂ Int |p1p4|
Int|p0p1p5|⊂Int|p0p1p4| など
L2について,
Int |p1p6p7| ⊂ Int |p1p3p4| など
[9]
重心細分
K(r) の重心細分を (K(r))’とすると, pσ をσの重心とすると,
(K(r))’= U pσ*K(∂σ)’ σ∈K
dimσ= r
と表せる細分を r=0 から dim K まで繰り返す。
例 3単体 (中身の詰まった四面体 )
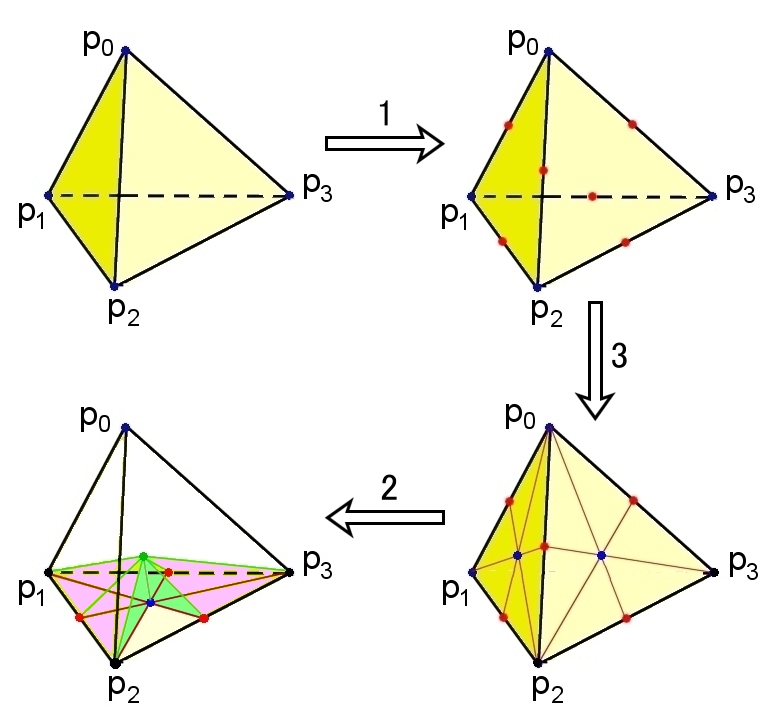 |
| 四面体の重心細分 面,体の分割結果は見やすいように一部分だけ示している。 |
四面体 頂点 線分 面 体 χ 1 分割前 4 6 4 1 1 2 線分の分割 10 12 4 1 1 3 三角形の分割 14 36 24 1 1 4 四面体の分割 15 50 60 24 1
ここで,χは単体複体のオイラー標数です。
オイラー標数については後で説明します。 ⇒ [#]
ここでは分割手順の説明をしておきます。
手順1 K(0)’の分割 = 不変
手順2 K(1)’の分割 = 辺を2分する
点の数 +6(辺の数)
線分の数 +6(辺数)
面の数 不変
体の数 不変
手順3 K(2)’の分割 = 三角形の重心と各点を直線で繋ぐ
点の数 +4(面の数)
線分の数 +24(1つの面内の頂点の数×面数=6×4)
面の数 =24((1つの面内の三角形の数×面数=6×4)
体の数 不変
手順4 K(3)’の分割 = 四面体の重心から各頂点を直線で繋ぐ
点の数 +1(四面体の重心の数)
線分の数 +14(四面体の(頂点数+辺数+面数=4+6+4)
面の数 +36(四面体の重心と1面の頂点を含む三角形の数
+四面体の重心と1面の辺を含む三角形の数÷2)×面数
=(6+6÷2)×4=36)
体の数 =24(四面体の1面の三角形数×面数=6×4=24
[1]
単体の条件を緩めた図形,すなわち,凸多角形,凸多面体のようにいくつかの半空間の共通部分として表される有界な図形を胞体といいます。厳密な定義は以下のとおり。
|
定義 胞体の定義 ΠをRn上のm次元空間とする。Π上の線形関数とは, f((1-t)p+tq)=(1-t)f(p)+tf(q) が任意の点 p,q∈Π,t∈R で成り立つことをいう。 PL(piecewise linear)についてはこちらを参照 ⇒ [#]Π上の線形関数を f1,f2,…,fk とするとき, C={ p∈Π|f1(p)≧0,f2(p)≧0,…,fk(p)≧0 } が空でない有界集合 (図形) ならば,Cをm次元胞体 (m胞体) という。 さらに, 内部 Int C={ p∈Π|f1(p)>0,f2(p)>0,…,fk(p)>0 } という。 面とは,複体における辺単体に対応する用語。 |
明らかに,
IntC ∪∂C =C かつ,IntC ∩ ∂C =φ
例
3単体は胞体である。
p0,p1,p2,p3 を通る3次元空間 Π,
p ∈ t0p0+t1p1+t2p2+t3p3 (t0+t1+t2+t3=1)
上の線形関数 fk:Π → R を
fk(p)=tk ( k=0,1,2,3 )
と定義すると,胞体Cは,
C= {p∈Π|fk(p)≧0 , k=0,1,2,3 }
={ t0p0+t1p1+t2p2+t3p3|t0+t1+t2+t3=1,tk ≧0 ( k=0,1,2,3 )}
=|p0p1p2p3|
であり,3単体 [#] でもある。
面については以下のものがある。
fk(p)=0 ( k=0,1,2,3 ) は,4つの面=2辺単体 からなり,境界を表す。
fj(p)=fk(p)=0 ( j,k=0,1,2,3 ;j≠k) は6つの辺=1辺単体。
fi(p)=fj(p)=fk(p)=0 i, j,k=0,1,2,3 ;j≠i,j≠k,i≠k) は4つの点=0辺単体。
[2]
また,次が成り立つ。
|
命題 胞体C の内部の1点を pcとすると,pc から伸びる半直線は∂Cと1点だけで交わり, C= pc*∂C が成り立つ。 胞体が凸な図形であるということの特徴。 |
[3]
胞体的複体
|
定義 胞体的複体 胞体的複体 とは,胞体の集合 M であって, (1) C∈M,D が Cの面 ⇒ τ∈M [面をすべて含む] (2) C,D∈M C∩D≠φ ⇒ C∩D は Cの面,かつ,C∩D は Dの面 を満たすこととする。 |
[4]
|
定理 任意の胞体的複体は単体的複体に細分できる。 |
ほぼ自明。
胞体的複体(X=直方体)の単体分割の例 (重心細分ではない例)
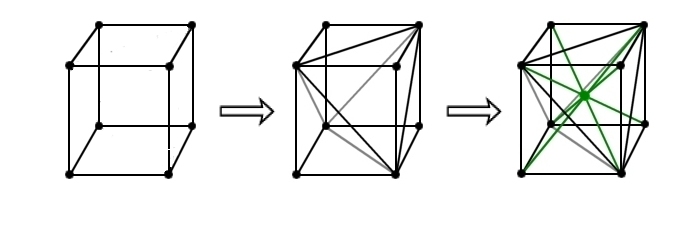
| 胞体 | 頂点 | 線分 | 面 | 体 | χ |
| 直方体 | 8 | 12 | 6 | 1 | 1 |
| 面の2分割後 | 8 | 18 | 12 | 1 | 1 |
| 体の12分割後 | 9 | 26 | 30 | 12 | 1 |
[5]
さらに,
|
定理 共通細分 複体 K1 と K2 が同じ多面体 X の異なる単体分割,すなわち,X=|K1|=|K2|ならば,K1 と K2との共通な細分(共通細分)L が存在する。このとき,dim K1 = dim K2 である。 |
例
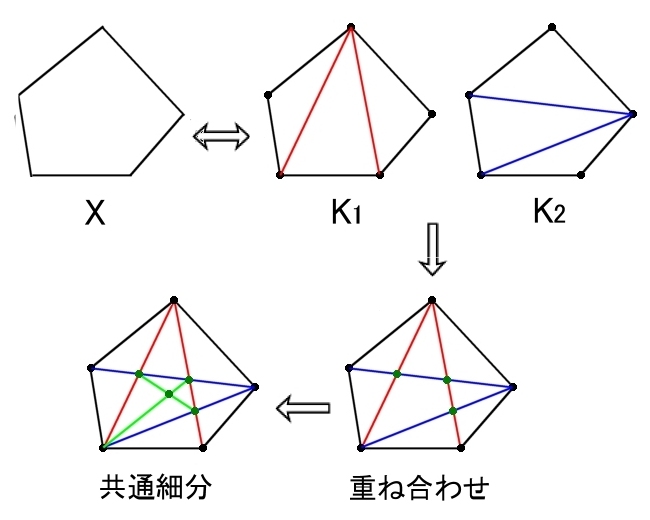
要するに,K1とK2を重ね合わせて,胞体となっている個所を単体に分割すれば,共通細分が得られます。
|
定義 オイラー標数 m次元複体 K に対して,αn(K) を Kの n単体の個数 とするとき, χ(K)=α0(K)−α1(K)+・・・+(-1)mαm(K) を複体Kのオイラー標数 という。 |
[7]
|
定理 複体 K1 と K2 が同じ多面体 X の異なる(単体)分割である,すなわち,X=|K1|=|K2|ならば,χ(K1)=χ(K2) である。 |
例 はすでに,X=四面体 [#],直方体 [#]の場合で示してあります。
[8]
|
定理 多面体 X と Y が位相同型ならば,χ(X)=χ(Y) である。 |
この証明は重要だがここでは省略して別の機会に紹介する。
[1] 先ず,単体から単体への線形写像について説明します。
単体σ
|p0p1…pm|={ p=t0p0+t1p1+…+tmpm|
t0+t1+…+tm=1,t0≧0,t1≧0,…,tm≧0 }
単体τ
|q0q1…qn|={ q=s0q0+s1q1+…+snqn|
s0+s1+…+sn=1,s0≧0,s1≧0,…,sn≧0 }
として,σからτへの写像 f が,
f(p)=f(t0p0+t1p1+…+tmpm)
=t0f(p0)+t1f(p1)+…+tmf(pm)
を満たすとき,f を線形写像といいます。
このとき,
(1) f は連続写像である
(2) σの任意の辺単体ρに制限した f |ρも連続な線形写像である。
ことは容易に確かめられます。
[2]
多面体の単体複体にこの線形写像を適用して次のようにPL写像を定義します。
|
定義 PL同型 多面体 X,Y の単体分割をそれぞれ,K,L とするとき,X から Y への写像 f が, (1) 単体τ∈L が存在して,f(σ)⊂τである。 であるとき,f をPL写像という。 さらに f が全単射であるならばPL同型写像といい,X と Y はPL同型であるという。 |
また,PL同型写像 f は連続写像でもあるので,同相写像 [#] でもある。
例1 PL写像 f : |X| (正方形) → |Y| (四角錐)
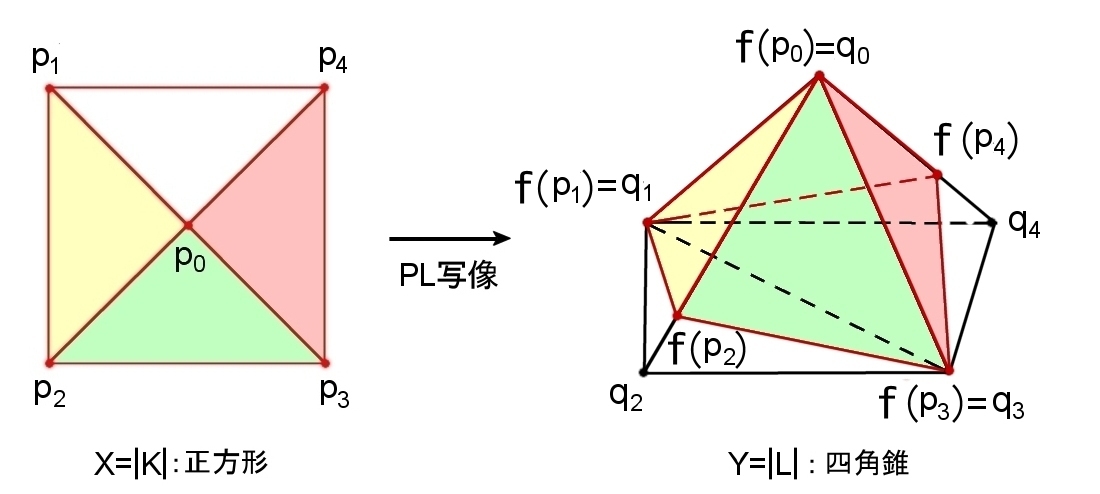
f(|p0p1p2|)⊂|q0q1q2|
f(|p0p4|)⊂|q0q4|
などと確かめることができる。
[3]
例2 PL同型写像写像
f : X → Y
g : Y → Z
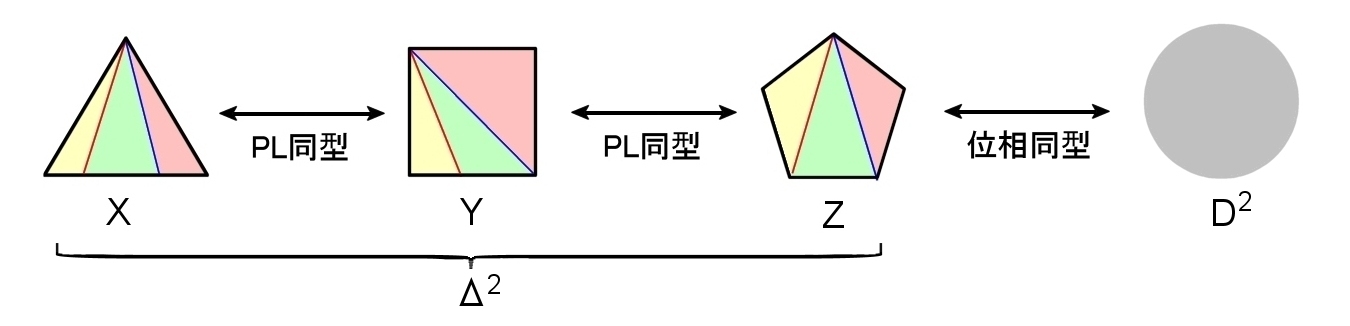
合成写像 fοg も PL同型写像
|X|=三角形,|Y|=四角形,|Z|=五角形 は互いにPL同相である。
三角形(2単体)にPL同型な図形を2次元PL円板といい,その境界を1次元球面といいます。
一般化して,
|
定義 (1) m単体σmにPL同型な多面体をm次元PL円板といい,Δmと書く。 (2) その境界∂σm にPL同型な多面体をm-1次元PL球面といい,Σm-1と書く。 |
これらは,位相空間の場合のm次元円板 Dm,m-1次元球面 Sm-1に対応しており,
Δm ⇔ Dm
Σm-1 ⇔ Sm-1
となりますが,厳密に使い分けずに表記されることもあります。
[4]
|
定義 星状複体とまつわり複体 (1) 多面体 |K| の1点 x を含んでいるすべての単体とそれらのすべての辺単体からなる K の部分複体を 星状複体 といい,Star(x;K)と書く。また,|Star(x;K)| を 星状多面体という。 (2) 星状複体に含まれる単体の中から x を直接含まない単体だけを選び出した集合をまつわり複体といい,Link(x;K)と書く。また,|Link(x;K)|をまつわり多面体という。 |
例
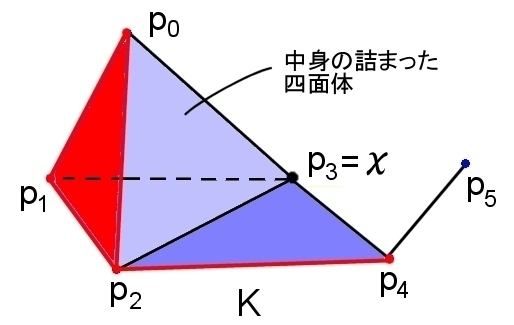
|Star(x;K)| は彩色部分
|Link(x;K)| は赤色で示した。
Star(x;K)={ |p0p1p2p3|,|p1p2p3|,|p0p2p3|,|p0p1p3|,|p0p1p2|,|p2p3p4|,
|p0p1|,|p0p2|,|p0p3|,|p1p2|,|p1p3|,|p2p3|,|p2p4|,|p3p4|,
|p0|,|p1|,|p2|,|p3|,|p4| }
Link(x;K)={ |p0p1p2|,|p0p1|,|p0p2|,|p1p2|,|p2p4|,|p0|,|p1|,|p2|,|p4| }
[5]
|
定義 境界のないPL多様体 (= PL閉多様体) 多面体 X に対して,ある単体分割 K が存在して,任意の x∈X の Link(x;K) が m-1次元PL球面 Σn-1であるとき,多面体 X を境界のないm次元PL多様体 という。 |
例
X=|K|=四面体表面は2次元PL閉多様体である。
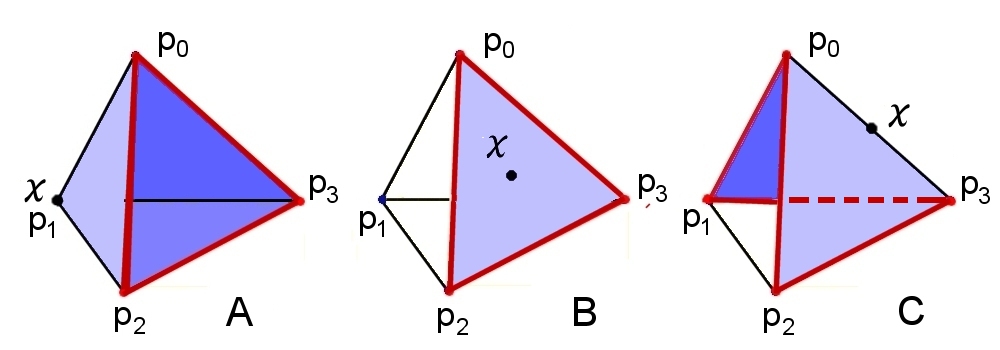
|Link(x;K)| は赤色で示したようにいずれの場合もΣ1である。
A x が頂点p1 のとき
Star(x;K)={ |p1p2p3|,|p0p1p3|,|p0p1p2|,
|p0p1|,|p0p2|,|p0p3|,|p1p2|,|p1p3|,|p2p3|,
|p0|,|p1|,|p2|,|p3| }
Link(x;K)={ |p0p2|,|p0p3|,|p2p3|,|p0|,|p2|,|p3| }
B x が三角形 |p0p2p3| の内点のとき
Star(x;K)={ |p0p2p3|,|p0p2|,|p0p3|,|p2p3|,|p0|,|p2|,|p3| }
Link(x;K)={ |p0p2|,|p0p3|,|p2p3|,|p0|,|p2|,|p3| }
C x が線分 |p0p3| の内点のとき
Star(x;K)={ |p0p2p3|,|p0p1p3|,|p0p1|,|p0p2|,|p0p3|,|p1p3|,|p2p3|,
|p0|,|p1|,|p2|,|p3| }
Link(x;K)={ |p0p1|,|p0p2|,|p2p3|,|p1p3|,|p0|,|p1|,|p2|,|p3| }
この2次PL閉多様体が,位相多様体の定義 [#] を満たしていることは,
任意の点xに対して,
U=|Star(x;K)|−|Link(x;K)|
考えると U が開集合であることから確認できます。
一般的にPL 多様体が位相多様体であることは正しいですが,逆に任意の位相多様体に同型なPL多様体が存在するかと言えば,高次元において成立しないことが分かっています。
[6]
|
定義 境界のあるPL多様体 多面体 X に対して,ある単体分割 K が存在して,任意の x∈X の Link(x;K) が m-1次元PL球面 Σn-1,または,m-1次元円板 Δm-1のいずれかである多面体 X を境界のある m次元PL多様体 という。 |
境界のないPL多様体,境界のあるPL多様体を合わせてPL 多様体とも言います。
例
X=|σ3|=三単体 (中身のある四面体) は境界のある3次元PL多様体である。
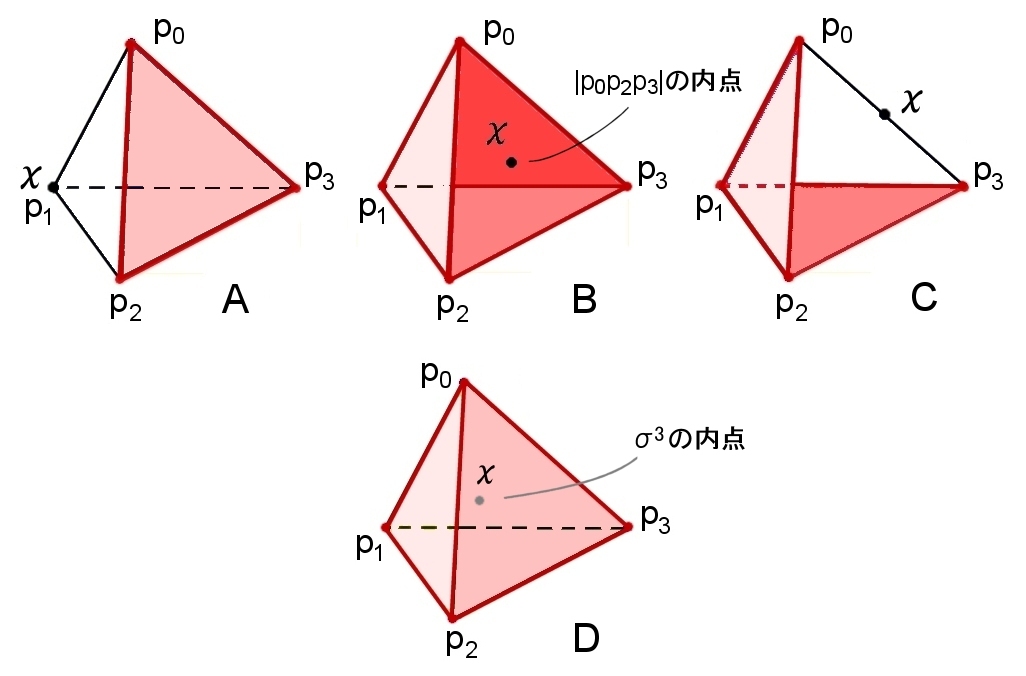
全てのケースで,
Star(x;σ3)=σ3 (3単体)
Link(x;σ3)=着色部分
A,B,Cのケースでは,
|Link(x;σ3)| 〜2次元円板 Δ2
Dのケースでは,
|Link(x;σ3)|=|∂σ3|=四面体表面 〜 2次元球面 Σ2
[7]
|
公式 X を m次元PL多様体,Y を n次元PL多様体とすると, (1) 直積 X×Y は (m+n)次元PL多様体である。 (2) X が境界をもてば,∂X は境界もたない (m-1)次元多様体である。 (3) Xが境界を持たなければ,∂X =φ (4) ∂(X×Y) = (∂X×Y) ∪ (X×∂Y) (5) ∂X×∂Y =(∂X×Y) ∩ (X×∂Y) |
例1
Δ1×Δ1は2次元PL多様体
Σ1×Σ1は2次元PL多様体 (PLトーラス)
例2
X=Δ1(赤線分),Y=Δ1(青線分)の場合
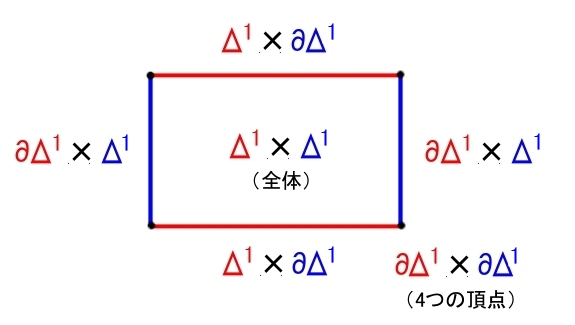
上図より公式(3)が確かめられる。
例3
Δ2×Σ1 は3次元PL多様体(中身の詰まったPLトーラス)であり,その境界は,
∂(Δ2×Σ1)=∂Δ2×Σ1=Σ1×Σ1
であり,PLトーラスである。