4 リーマン曲率テンソル |
||
| f-denshi.com 最終更新日: 校正中 | ||
| サイト検索 | ||
リーマン曲率テンソルを用いて曲面の曲がり方を定式化します。簡単な考察から,円錐側面や円筒側面と球面とでは,曲がっていると言っても本質的な違いがあることが分かります。円筒側面ははさみで上端から下端まで切ってやると歪ませることなく,それを広げて平坦な図形とする(平面に投影する)ことができます。ところが,球面はどのように有限箇所を切リ割いても決して,平坦な図形にはなりません (平面に歪なくして投影できない)。
[1] Ak を xi,次に xj で2回続けて共変微分することを考えます。2 回続けて共変微分するのですが,その際,1 回微分するとテンソルの階数が1 づつ増えていくことに注意する必要があります。ここですべきことは公式に当てはめて計算するだけですが,添え字がたいへん煩わしいので,少しずつ必要な数式を書きだしながら進めていきましょう。ベクトルを共変微分すると,(2.149) 式から,
Ak;i= ∂Ak −Γnki An xi で微分,指標 k,i の2 階共変テンソル ∂xi
Ak;j= ∂Ak −Γnkj An xj で微分,指標 k,j の2 階共変テンソル ∂xj
となりますが,これらは2 階テンソルでした。一方,2階共変テンソルTki を xj で共変微分,またはテンソルTkj をxi で共変微分すると,
∇jTki=Tki;j = ∂Tki −ΓpkjTpi −Γqij Tkq (2.231) ∂xj
∇iTkj=Tkj;i = ∂Tkj −ΓpkiTpj −Γqji Tkq (2.232) ∂xi
と書けますが,ここで,ベクトルA の共変微分を添え字を次のように対応させます。
Tki ← Ak;i= ∂Ak −Γnki An ∂xi
Tkj ← Ak;j= ∂Ak −Γnkj An ∂xj
Tpi ← Ap;i= ∂Ap −Γnpi An ∂xi
Tpj ← Ap;j= ∂Ap −Γnpj An ∂xj
Tkq ← Ak;q= ∂Ak −Γnkq An ∂xq
これら5式を (2.231),(2.232) に代入すると,次のテンソルが得られます。
[2]
(1) ベクトルAk を xi で微分してから,次に xj で微分した Aki;j は
∇jAk;i=Aki;j =∇j∇iAk
= ∂ ∂Ak −Γnki An −Γpkj ∂Ap −Γnpi An −Γqij ∂Ak −Γnkq An ∂xj ∂xi ∂xi ∂xq
(2) ベクトルAk をxj で微分してから,次にxi で微分したAk j ;i は,
∇iAkj=Akj;i =∇i∇jAk
= ∂Akj ∂Ak −Γnkj An −Γpki ∂Ap −Γnpj An −Γqji ∂Ak −Γnkq An ∂xi ∂xj ∂xj ∂xq
この2式の差を交換子と言います。緑字以外の項は相殺され,残る項は,
(∇j∇i−∇i∇j)Ak
= − ∂Γnki An+ ∂Γnkj An+ΓpkjΓnpi An −ΓpkiΓnpj An ∂xj ∂xi
= ∂Γnkj − ∂Γnki +ΓpkjΓnpi −ΓpkiΓnpj An ∂xi ∂xj
=Rnkij An
[3] ここで( )の部分,Rnkij をリーマン曲率テンソルと呼びます。
|
【定義27 】 リーマン曲率テンソル
|
|||||||||||||||
この値が 0 であれば,その空間が平坦であることを示し,0 でない場合は空間が曲がっていると解釈されます。
同様な計算を反変ベクトルに対して行うと,
(∇j∇i−∇i∇j)Ak =Ahi; j. −Ahj;i =−Rhmij Am (2.242)
を導くこともできます。交換子は共変微分の記号 [∇j,∇i] = ∇j∇i −∇i∇j を用いて書くと,
|
【公式7 】 ベクトルの共変微分の交換関係 [∇j,∇i] Ak = RnkijAn ⇔ [∇i,∇j] Ak = − RnkijAn |
[4] 混合テンソルであるリーマン曲率テンソルに次のように計量テンソルを掛けて4 階共変テンソルに降階した,
Rnkij = gmn Rmkij [ リーマン - クリストッフェルのテンソル ]
をリーマン - クリストッフェルのテンソルと言います。
リーマン曲率テンソルの定義式 (2.241) から明らかに次のような指標の交換に対する反対称性,対称性が存在します。
|
【公式8 】 リーマン曲率テンソルの指標の交換関係 Rnkij = - Rnkji [ i とj の交換] (2.246) |
2階テンソルの共変微分の交換関係は次のとおりとなります。(要チェック)
|
【公式9 】 2階テンソルの共変微分の交換関係 [∇j,∇i] Tks = Rnkij Tns + Rnsij Tkn (2.249) |
証明 ⇒ [#]
Tij= AiBj と置いて共変微分を丁寧に計算すれば,示すことができます。
特に Tkn = ∇kAs,Thk = ∇kAh の場合は,
|
【公式10 】 (テンソルの共変微分)の共変微分の交換関係 [∇j,∇i] ∇kAs = Rnkij∇nAs + Rnsij∇kAn (2.252) |
証明 ⇒ [#]
SUSTAINABLE TOKIWADAIGAK SINCE 2002
[1] 抽象的な話が続きましたので,具体的に球面のリーマン曲率テンソル
Rnkij= ∂Γnkj − ∂Γnki +ΓpkjΓnpi−ΓpkiΓnpj (2.254) ∂xi ∂xj
を求めてみましょう。
この定義式において,p が縮約をとるダミーの添え字であることから,n,k,i,j の各添え字がθ,φの2 通りの値をとる,すなわち,次の24 = 16 個の項が現れます。それらは以下のとおり,
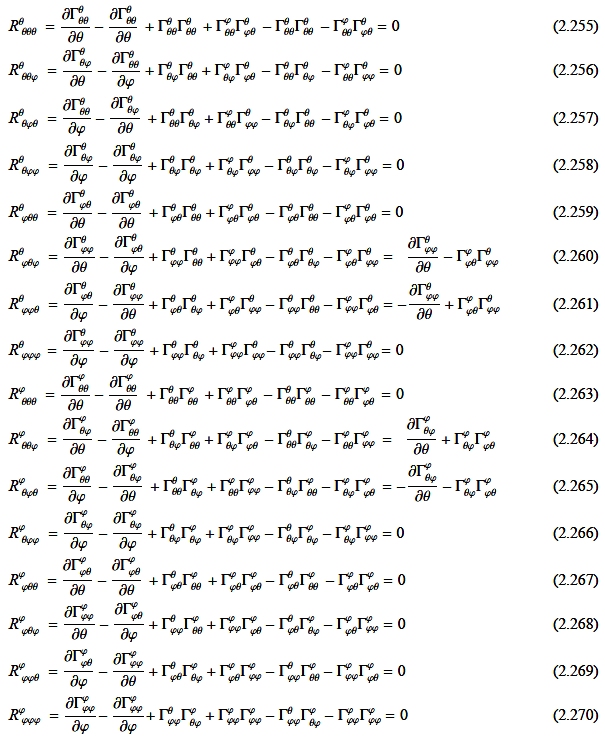
先に計算したクリストッフェル記号の値⇒[#] を用いて計算すると,0 でないものは,
Rθφθφ= ∂Γθφφ −ΓφφθΓθφφ ∂θ
=(sin2θ−cos2θ)−(−cos2θ)= sin2θ
Rθφφθ=− ∂Γθφφ +ΓφφθΓθφφ ∂θ
=−(sin2θ−cos2θ)+(−cos2θ)= − sin2θ
Rφθθφ= ∂Γφθφ +ΓφθφΓφφθ ∂θ
=− sinθ + cos2θ +cot2θ= −1 sinθ sin2θ
Rφθθφ=− ∂Γφθφ −ΓφθφΓφφθ ∂θ
= sinθ + cos2θ −cot2θ= +1 sinθ sin2θ
以上の結果を行列を用いてタイプごとにまとめると,
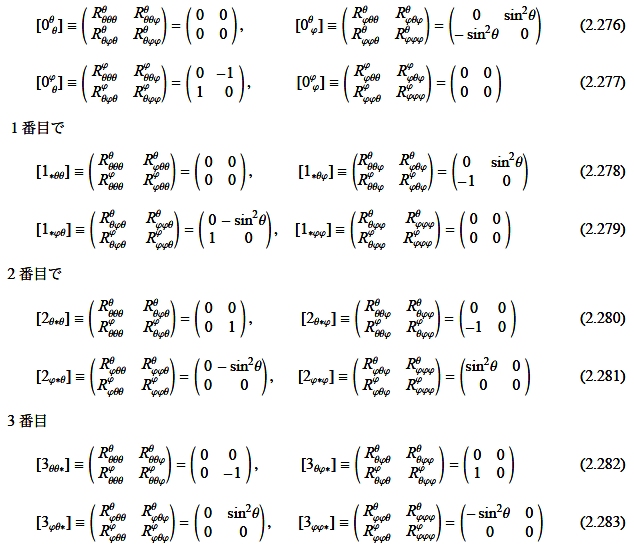
[2] ここで対称性を見るために計量を掛けて添え字を下げると,
Rnkij=gnpRpkij
ただし,
gθθ=r02 ,gφφ=r02 sin2θ, gθφ= gφθ= 0 (2.284)
などと計算して,
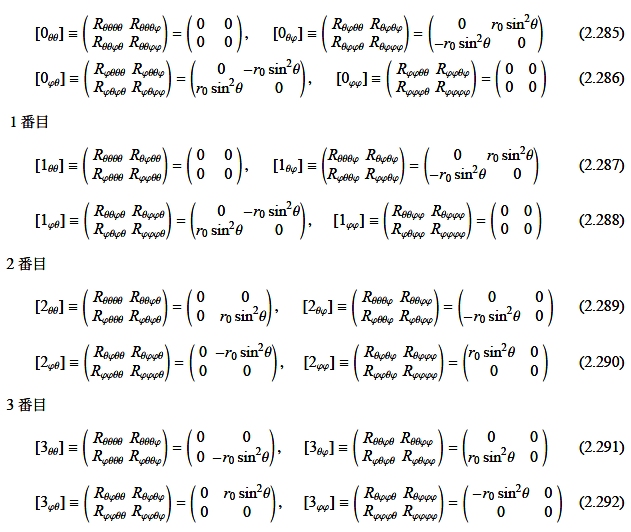
となります。
曲率テンソルの指標の交換に対する対称性 (公式8) を確認しておくと,
Rnkij = −Rnkji [ i とj の交換] ⇒ [0nk], [1nk] が反対称行列 (2.293)
Rnkij = −Rknij [ n とk の交換] ⇒ [Rnk] =−[Rkn] (2.294)
Rnkij = +Rijnk [ (nk) と(i j) の交換] ⇒ [N] が対称行列
(2.295)
ただし,3つ目の関係は,4 つの [Rmn] (R=0,1,2,3) から同じ行,同じ列の要素を抜き出して,以下の行列 [R*mn] を新たに定義すると,
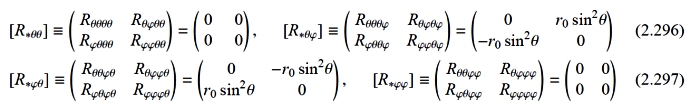
ここで,[Rmn] = [R*mn] が成立していることを意味しています。
[1] 円筒側面のリーマン曲率テンソルを計算します。
まず,直交座標(x, y, z) と円筒座標(φ, Z) との関係は,r0 を定数として,
x = r0 cosφ (2.298)
y = r0 sinφ (2.299)
z = Z (2.300)
これより,円筒座標系の基底を正規直交基底で展開 [#] したときの成分は,
eφ= ∂x ex+ ∂y ey+ ∂z ez = -r0 sinφ,r0 cosφ,0 ∂φ ∂φ ∂φ
eZ = ∂x ex+ ∂y ey+ ∂z ez = 0,0,1 ∂Z ∂Z ∂Z
したがって,
gφφ=eφ・eφ= r02sin2φ+r02cos2φ = r02
gφZ=eφ・eZ = -r0sinφ・0+r0cosφ・0+0・1 = 0 (= gZφ )
gZZ =eZ・eZ = 0・0+0・0+1・1 = 1
すなわち,半径r0 の2次元円筒側面の計量テンソルの成分
G = gφφ g1φZ = r02 0 gZφ gZZ 0 1
r0 = 定数> 0 (2.302)
これより,いずれの計量も定数なので,すべてのクリストッフェル記号の値は 0 です。
Γuij= 1 gku ∂gik + ∂gjk − ∂gij 2 ∂xj ∂xi ∂xk
= 0 (n, k, i, j = .φまたは,Z) (2.303)
当然,リーマン曲率テンソルも 0 です。
Rnkij= ∂Γnkj − ∂Γnki +ΓpkjΓnpi−ΓpkiΓnpj = 0 ∂xi ∂xj
このように歪のない平面展開図が存在する図形は,計量テンソルがすべて定数となるためリーマン曲率テンソルは0
となることが分かります。
SUSTAINABLE TOKIWADAIGAK SINCE 2002
[1] これも当たり前のことの確認です。 2 次元平面を極座標で表した座標
x=r cosφ
y=r sinφ
極座標の基底は正規直交座標の基底で展開すると
er= ∂x ex+ ∂y ey= cosφ,sinφ ∂r ∂r
eφ= ∂x ex+ ∂y ey= -r sinφ,r cosφ ∂φ ∂φ
grr=er・er=(cosφ)2+(sinφ)2=1
gφφ=eφ・eφ=(-r sinφ)2+(r cosφ)2=r2
gφr=eφ・er= - r sinφcosφ+r cosφsinφ=0 =grφ
したがって,計量テンソルは,
G = grr grφ = 1 0 gφr gφφ 0 r2
G-1= grr grφ = 1 0 gφr gφφ 0 1/r2
これを用いて,クリストッフェル記号を計算します。
[2] 例えば,
| Γrφφ= | 1 | gkr | ∂gφk | + | ∂gφk | − | ∂gφφ | |||||
| 2 | ∂φ | ∂φ | ∂xk |
| = | 1 | grr | ∂gφr | + | ∂gφr | − | ∂gφφ | + | 1 | gφr | ∂gφφ | + | ∂gφφ | − | ∂gφφ | ||||||||||
| 2 | ∂φ | ∂φ | ∂r | 2 | ∂φ | ∂φ | ∂φ |
| = | 1 | ・1・(0+0-2r) | + | 1 | ・0・(…) = - r |
| 2 | 2 |
| Γrrφ= | 1 | gkr | ∂grk | + | ∂gφk | − | ∂grφ | |||||
| 2 | ∂φ | ∂r | ∂xk |
| = | 1 | grr | ∂grr | + | ∂gφr | − | ∂grφ | + | 1 | gφr | ∂grφ | + | ∂gφφ | − | ∂grφ | |||||||||
| 2 | ∂φ | ∂r | ∂r | 2 | ∂φ | ∂r | ∂φ |
| = | 1 | ・1・(0+0−0) | + | 1 | ・0・(…) = 0 |
| 2 | 2 |
| Γφrφ= | 1 | gkφ | ∂grk | + | ∂gφk | − | ∂grφ | |||||
| 2 | ∂φ | ∂r | ∂xk |
| = | 1 | grφ | ∂grr | + | ∂gφr | − | ∂grφ | + | 1 | gφφ | ∂grφ | + | ∂gφφ | − | ∂grφ | |||||||||
| 2 | ∂φ | ∂r | ∂r | 2 | ∂φ | ∂r | ∂φ |
| = | 1 | ・0・(…) | + | 1 | (1/r2)(0+2r+0) = 1/r |
| 2 | 2 |
他も計算して,行列を利用してまとめると,
Γrrr Γrrφ = 0 0 Γrφr Γrφφ 0 -r
Γφrr Γφrφ = 0 1/r Γφφr Γφφφ 1/r 0
リーマン曲率テンソルは,二つほど計算してみると,
Rrφrφ= ∂Γrφφ − ∂Γrφr +ΓpφφΓrpr−ΓpφrΓrpφ ; p=r,φ ∂r ∂φ
= −1− 0 +{ (−r)×0 +0×0 }−{
0×0+(1/r)×(-r) } = 0 (2.309)
Rφrrφ= ∂Γφrφ − ∂Γφki +ΓprφΓφpr−ΓprrΓφpφ ; p=r,φ ∂r ∂φ
= -(1/r2)−0+{ 0×0 +(1/r)×(1/r) }−{ 0×(1/r)+0×0 } = 0
とゼロとなります。残り14個のリーマン曲率テンソルも同様に計算して0 を確かめられます。
平面のリーマン曲率テンソルを極座標で計算しても,
Rnkij = 0
つまり,「平面に極座標を導入しても平面が曲がっていることにはならない。」というもっともな結論となります。
捕捉: 後ほど述べるようにリーマン曲率テンソルの(反)対称性から2次元曲面のリーマンテンソルの自由度が1であることを考慮すれば,さらに計算を進めることなく,他のリーマン曲率テンソルの値が 0 であることも分かります。