5 アインシュタインテンソル |
||
| f-denshi.com 最終更新日: 校正中 | ||
| サイト検索 | ||
|
【公式11 】 ビアンキの恒等式 Rnkij + Rnjki + Rnijk = 0 (2.321) ∇kRnsij+∇jRnski+∇iRnsjk = 0 (2.322) |
【公式10 】 テンソルの共変微分の交換関係より,
[∇j, ∇i]∇kAs = Rnkij∇nAs + Rnsij∇kAn (2.314)
共変微分の順序を次のように換えて,
∇k[∇j,∇i] As = ∇k(RnsijAn)
= (∇kRnsij)An + Rnsij∇kAs (2.315)
これら2 式の差をとると,第2項どおしがキャンセルされて,
[∇k[∇j,∇i]]As = ∇k[∇j,∇i] As − [∇j,∇i] ∇kAs
= (∇kRnsij)An − Rnkij∇nAs (2.316)
添え字,i, j, k を順送りにした同様な式を書き下ろすと,
[∇j[∇i,∇k]]As = (∇jRnski)An − Rnjki∇nAs (2.317)
[∇i[∇k,∇j]]As = (∇iRnsjk)An − Rnijk∇nAs (2.318)
添え字,i, j, k を順送りにした上の3 式を辺々足すと,
{ [∇k[∇j,∇i]]+[∇j[∇i,∇k]]+[∇i[∇k,∇j]] } As
= (∇kRnsij+∇jRnski+∇iRnsjk) An−(Rnkij+Rnjki+Rnijk)∇nAs (2.319)
この左辺はヤコビの関係式 [#] であって,(括弧を外してバラせばすぐに分かる。)
[∇k[∇j,∇i]] + [∇j[∇i,∇k]] + [∇i[∇k,∇j]] = 0 (2.320)
となります。したがって,等式(2.319) が任意のベクトルAn,∇nAs について成立するためには,
|
【公式11 】 ビアンキの恒等式 Rnkij + Rnjki + Rnijk = 0 (2.321) ∇kRnsij+∇jRnski+∇iRnsjk = 0 (2.322) |
が成り立つ必要があります。
ビアンキの第2 恒等式を変形することで,アインシュタインテンソルを導くことができます。計量を用いてビアンキの第2 恒等式を次のように書き換えます。
∇kRnsij + ∇jRnski + ∇iRnsjk = 0 (2.325)
↓ gnm をかけて (∇k gnm = 0 に注意 )
∇k gnmRnsij + ∇j gnmRnski + ∇i gnmRnsjk = 0 (2.326)
↓ 縮約
∇kRmsij + ∇j Rmski + ∇i Rmsjk = 0 (2.327)
↓ gsk をかける
∇k gskRmsij + ∇j gskRmski + ∇i gskRmsjk = 0 (2.328)
↓ 縮約
−∇k Rkmij− ∇j Rmi + ∇i Rmj = 0 (2.329)
↓ gmj をかける
−∇k gmjRkmij− ∇j gmjRmi + ∇i gmjRmj = 0 (2.330)
↓ 縮約
−∇kRki− ∇j Rj i + ∇i R = 0 (2.331)
↓ 縮約の添え字を m にそろえる,∇i → ∇mδmi
−2∇mRmi+ ∇mδmi R = 0 (2.332)
↓ −2 で割り,ginをかける
∇m ( ginRmi− 1 δmiginR )= 0 (2.333) 2
↓ 縮約
∇m ( Rmn − 1 gmnR )= 0 (2.334) 2
ここで,最後の( ) の中の式を,アインシュタインテンソルと定義します。
|
【定義28 】 アインシュタインテンソル
|
アインシュタインテンソルについては後ほど改めて説明します。
リーマン曲率の添え字n とi とで縮約をとった
|
【定義29 】リッチテンソル (2 次元の場合)
|
をリッチテンソルといいます
例 2次元球面のリッチテンソル
球面の計量と16個のリーマン曲率テンソルをもう一度書いておくと,
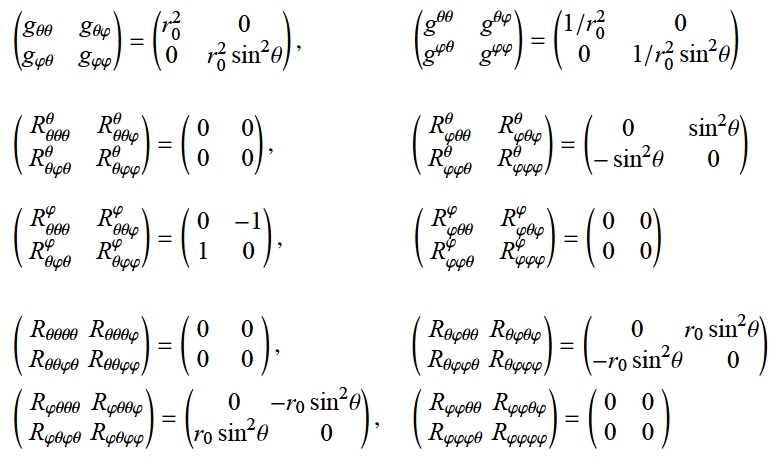
これらを利用して,
Rkj = Rnknj = Rθkθj + Rφkφj (2.348)
を計算すればよい。結果は,
| = | = | ||||||||||
| Rθθ | Rθφ | = | Rθθθθ+Rφθφθ | Rθθθφ+Rφθφφ | |||||||
| Rφθ | Rφφ | Rθφθθ+Rφφφθ | Rθφθφ+Rφφφφ |
| = | 0+1 | 0+0 | |||
| 0+0 | sin2θ+0 |
| = | 1 | 0 | |||
| 0 | sin2θ |
(2.349)
添え字を上げた場合も計算しておくと,
| Rθθ | Rθφ | = | gθθRθθ+gθφRφθ | gθθRθφ+gθφRφφ | |||||||
| Rφθ | Rφφ | gφθRθθ+gφφRφθ | gφθRθφ+gφφRφφ |
| = | 1/r02×1+0×0 | 1/r02×0+0×sin2θ | |||
| 0×1+1/sin2θ×0 | 0×0+1/r02sin2θ×sin2θ |
| = | 1/r02 | 0 | |||
| 0 | 1/r02 |
(2.350)
さらに添え字を上げて,
| Rθθ | Rθφ | = | gθθRθθ+gθφRθφ | gθθRφθ+gθφRφφ | |||||||
| Rφθ | Rφφ | gφθRθθ+gφφRθφ | gφθRφθ+gφφRφφ |
= 1/r02×1/r02+0×0 1/r02×0+0×1/r02 0×1/r02+1/sin2θ×0 0×0+1/r02 sin2θ×1/r02
= 1/r04 0 0 1/r04 sin2θ
まとめ
さらに,リッチテンソルから添え字を上にあげて,縮約すると,
|
【定義30 】 リッチスカラー R = gkjRkj (= Rjj = R11+ R22 ) (2.352) |
例
2次元球面のリッチテンソル [#] からリッチスカラーを計算します。
R=gθθRθθ+gθφRθφ+gφθRφθ+gφφRφφ
= 1 ×1+0×0+0×0+ 1 ×sin2θ r02 r02 sin2θ
= 2 r02
あるいは,
R=gθθRθθ+gθφRθφ+gφθRφθ+gφφRφφ
=r02× 1 +0×0+0×0+r02 sin2θ 1 r04 r04 sin2θ
= 2 r02
または,混合テンソル(2.350) の対角和より,
R=Rθθ+ Rφφ
= 1 + 1 r02 r02
= 2 r02
以上,3 通りの方法で求めてみました。なお,得られた結果ですが,2 次元球面に限らず,n 次元曲面のリッチスカラーR は,微分幾何学的な方法で計算される「ガウス曲率 K」(微分幾学参照) と次の関係,
R = n(n − 1) K
↓ 球面の場合
R = 2K
で結び付けられています。ちなみに。球面のガウス曲率は 1/r02 です。
また,2 次元のリーマン曲率テンソルとリッチスカラーとの関係
2R1212 = R (g11g22−(g12)2)
↓ 球面の場合
2×Rθφθφ = R ( gθθgφφ−(gθφ)2 )
⇔ 2×r02 sin2θ= 2 (r02×r02 sin2θ−02) r02
例 球面のアインシュタインテンソル
Gmn = Rmn - 12gmnR (2.358)
を計算してみます。ここで,Rmn,gmn,R は以下の通りでした。
Gmn =
| = | Rθθ | Rθφ | − |
|
gθθ | gθφ | ×R | ||||||||||
| Rφθ | Rφφ | gφθ | gφφ |
| = | 1/r04 | 0 | − |
|
1/r02 | 0 | × |
|
||||||||||||
| 0 | 1/r04 sin2θ | 0 | 1/r02 sin2θ |
| = | 0 | 0 | ||||
| 0 | 0 |
(2.359)
つまり,2次元球面のアインシュタインテンソルの成分はすべてゼロです。一般に,「2次元空間のアインシュタインテンソルは 0 である」 ことが分かっています。
まず,最初にアインシュタインテンソルの定義を示しておきましょう。
Gmn = Rmn − 1 gmnR (2.360) 2
ここで,Rmn,および,R はミンコフスキー空間におけるリッチテンソルとリッチスカラー,また,gmn は計量テンソルです。したがって,それらを組み合わせたアインシュタインテンソルとは一種の曲率テンソルです。そして,このアイシュタインテンソルとエネルギー運動量テンソルTmn を結びつけることて,アイシュタインの一般相対性理論におけるアインシュタイン方程式が次のように提示されます。
Gmn = 8πG Tmn (2.361) c4
G は重力定数,c は光速度です。つまり,空間にエネルギーすなわち質量が存在するときに空間がどの程度曲がっているかを示しているのがアインシュタイン方程式というわけです。
概略は以上のとおりですが,ミンコフスキー空間とエネルギー運動量テンソルについてはAppendixに簡単に説明しています。
エネルギー運動量テンソルの共変微分 → Appendix