６　電気変位　［電束密度］
f-denshi.com  [目次へ]　最終更新日：06/06/18
サイト検索

　真空中に数個の点電荷を扱うならば，クーロンの法則をそのまま用いた取り扱い（ 連立微分方程式を解く ）も可能です。もちろん厳密解となると，３体問題と同じ困難さをともないますが・・・今の時代はコンピュータで数値計算することもできますが。 しかし，電荷が連続的に分布しているとみなせるほどの多数の荷電粒子の集まり（＝巨視的な物質）の電気的特性を扱う場合は，新たな変数（物理量）D を導入した方がずっと便利になります。ここでは平板コンデンサーを実例にとり，物質の電気的な特性を記述するために必要な変数 をいくつか導入し，その意味や利用方法を説明します。

１．コンデンサーと電気変位　（＝D　）

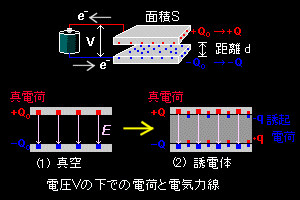
［１］　導体板でできた平板コンデンサーを考えます。右下図のように面積 S の導体（電極）が距離 d の間隔を空けて平行に置かれ，電池（直流電源）によって両端に一定の電圧 V がかけられ，正極板には+Q，負極板には-Qの電荷が蓄えられて釣り合っているとします。また，面積 S に較べて距離 d が小さく　(　S-1/2 ＞＞ d　)，かつ電圧 V が比較的小さく，電極板の間だけに均一な電場 E  ができているとします。すると，次の関係，

（１）隙間が真空のとき，

Q0 ＝ C0V，　　　･････（１）　 ←　とりあえず，実験式と考えてください。
ES ＝ Q0  　　 ･････（２）　← ガウスの法則から
ε0
V ＝ E ・d           ･････（３）

などが成り立ちます。ここで，ε0 は真空中の誘電率[#]，C0 は（真空中の）静電容量と呼ばれるものです。 C0 はこれらの式から Q0，V を消去して，

C0 ＝ ε0S
d

と書くこともできます。つまり，コンデンサーに蓄えられる電気量は電極面積に比例して大きくなり，単位は［C/V］ですが，[F］（ファラッドと読む）が一般的に使われます。

［２］　

（２）隙間が等方的な誘電体のとき，

同じ条件下で導体板のすき間に等方的で均質な誘電体（空気，電解液など）を挿入すると，真空の場合に比べて静電容量（＝真電荷）の増加： Q0 → Q が観測されます。しかし，蓄えられる電気量と電圧との間には依然として比例関係が成り立ち，その静電容量をCとすれば，

Q ＝ CV，

が成り立つとします。この変化の理由を電極間の誘電率が変化したためと解釈することもできますが，ここでは微視的に考えて，

「誘電体が存在すると，
正極側の誘電体表面にはマイナス電荷が誘起され，正極上のプラス電荷をより安定化し，
負極側では反対のことが起こり，等量のマイナス電荷がより安定化されるため。」

と解釈することにします（右上図参照）。この誘起された電荷量をそれぞれ +q ，-q とし，この q と誘電体挿入前の電荷 Q0 との比を

　比電気感受率　χ r ＝ q
Q0

と定義しておきましょう。　　（ ちなみに，電気感受率(electric susceptibility)： χ≡ ε0χ r　[F/m] ）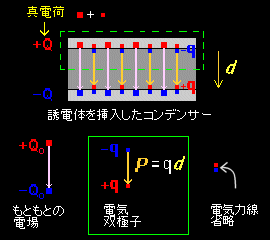

［３］　さて，右図は電極板の間に等方的な誘電体を挿入した時の様子を拡大したものです。破線で囲った部分について，ガウスの法則[#]を適用すると，電極間にしか電場が存在しないことに注意して，

　E ・S ＝ （ Q−q ）/ε0　　　　　　　　　

を得ます。これを，右辺に真電荷 Q だけが残るように，

ε0E ・S ＋q ＝ Q　　

と変形し，さらに，この左辺を，

[ 左辺 ]　＝ （ ε0E ＋q / S ） S
　　　　　　＝ （ ε0E ＋P ） S
　　　　　　＝ D ・S     ＝ Q (真電荷)＝[右辺]

と変形していきます。ここで，

q ⇒　P   ・・・（４）  ［←分極，または電気分極（の大きさ）］
S
ε0E ＋ P ⇒　D   ・・・（５）  ［←電気変位または電束密度（の大きさ）］

を定義して用いました。分極 (electric polarization) P，電気変位 (electric displacement) D の単位はともに　［Cm-2］　です。

［４］　この P と D は，大きさだけでなく方向も考慮したベクトル表記 （ P，D と書く ） が可能です。特に真空中では，P ＝0 　（q ＝ 0 なので） なので（５）式は，

D ＝ ε0E 　　　　　　　　［真空中］

と書けます。

［５］　一方，電極すき間に等方的な誘電体が存在するときの誘電体表面に誘起されたマイナス電荷から反対極板表面のプラス電荷を指すベクトルd  を考えると[#]，この方向は電場ベクトルE と同じ方向（ +Q から -Q への方向 ）なので　(等方的な誘電体でない場合，E とd は必ずしも同じ方向を向かないのでテンソル表記が必要) ，分極のベクトル表示は，
　　

　P　＝ （ q / S ） ･ （d /d ）  ←　（４）に方向を考慮してベクトル化，×（d /d ）［単位ベクトル］
　　＝ （χ r Q0 / S）d / d　  ←比電気感受率の定義[#] から
　　＝ （χ r ε0E ）d / d　    ←ガウスの法則（２）　[#]　から
　　＝ χ r ε0E　　　　　　  　←｜d / d｜＝ 1でE　と同じ方向 (等方的誘電体) なので
    ＝ χE                ･････　（６）  

すなわち，

  P　＝χE  

と書くことができます。ここの最後の（６）で，電気感受率，

χ≡ ε0χ r 　　　[F/m]　または，[C/(Vm)]

を定義して導入しました。

ちなみに，（４）式を見れば，|P｜= ［Cm-2］は誘電体表面に誘起された面電荷密度 |q/S| ですが，
P　＝ （ q/ S ）( d / d ）
　　＝ qd / （Sd）
　　＝p / V0，  V0：電極間の体積　
と変形すれば，
分極 P [C/m2]は双極子モーメントp＝qd  [Cm] の体積密度[(Cm)/m3]
とも解釈できることがわかります。

[5.1] これらの関係を用いれば，（５）式で示した等方的な誘電体の電気変位（電束密度）D  は，ベクトル表記で，　

D ＝ ε0E ＋P
　　＝ε0E ＋χE
　　＝ （ε0 ＋ε0χr） E
　　＝ εE

すなわち，

D　＝ε0E ＋P ＝εE  

となります。 ただし，＝のところで定義したε[F/m] は，挿入した誘電体の誘電率(permittivity, dielectric constant)と呼ばれ，

ε ＝ （1＋χr）ε0 　　　　　　誘電率　

という関係があります。 また，ε/ε0 ＝（1＋χr） を

εr 　≡ ε ＝ 1＋χr　　　　　比誘電率
ε0

と書いて比誘電率といいます。  

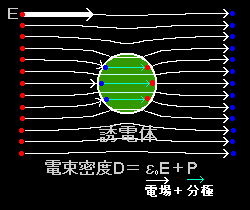
右上には一様な外部電場E の中に十分に長い円筒形の誘電体を電場と垂直方向に向けて置いたときにできる電気変位，分極，電気力線の概観を断面図で示しています。

「電気力線（電場Ｅ）が不連続であるのに電気変位D （電場＋分極）は途切れることのない連続曲線となる。」

ことに注目して下さい。

［６］　また，電気変位 D ＝εE  を用いて，ガウスの法則 [#] は，

 D ･ dS ＝ Q　［真電荷］　⇔　 E ･ dS ＝ Q/ε

と書けることはすぐにわかります。D･S ＝ Q でしたね[#]。ここで，ε＝（1＋χr）ε0と定義したεとクーロンの法則におけるεが対応していることを確認してください。さらに，この右辺を閉曲面内の真電荷密度；ρを用いて，

Q  ⇒ ρdV

と書き，左辺についてはベクトル解析におけるガウスの定理[#]を用いて書き直すと，

D･dS  ⇒ divD dV

なので，体積積分で表した両辺の中身を等しいとして，３．[#] で結果だけ書いておいた「ガウスの法則の微分形」と呼ばれる表現が得られます。

div D　＝ ｄｉｖ（ε0E ＋P ） ＝ ρ　　　　　［ガウスの法則の微分形］

なお，ρp ≡−ｄｉｖP　を分極電荷密度と定義して用いることもありますので，ついでに覚えておきましょう。このとき，微分形のガウスの法則は，

ｄｉｖ ε0E ＝ρ＋ρp 　　(＝真電荷密度＋分極電荷密度)

[７]　　電気変位と分極との関係

D　＝εE  

 P　＝χE D　＝ ε0E ＋P [C/m2]
εr 　≡ Q0＋q
Q0
χr ＝ q
Q0
εr ＝ 1＋χr 無次元
ε＝ε0εr χ≡ ε0χr　 ε＝ε0＋χ [F/m]

実はこの辺のところ，教科書によって用語・記号が統一されていない。ときわ台学において比電気感受率χrとしている量を単に電気感受率χとしている教科書も多い。



２．変位電流

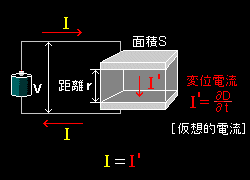
［１］　右のような回路において，静電容量 C の平板コンデンサー（ 誘電率 ε ）に電荷が蓄えられていく充電過程を考えます。この過程は，もちろん一瞬にして電極板に電荷が出現するわけでなく，電池から時間をかけて電荷が送りこまれてゆくのでリード線には電流（ I ）が観測されます。また，正負電極板の間には真の電流（荷電粒子の併進運動）は存在しないのですが，電気回路的にみれば，あたかもリード線中と同じ大きさの電流 Ｉ （ ＝ I ） が流れているみなすことも可能です。　この仮想的電流を変位電流と言います。

では，この電流値 Ｉ を求めてみましょう。　電極両端に現れる真電荷量を Q，電束密度（電気変位）を D とすると，Q ＝ DS　であることに注意すれば[#]，リード線に流れる電流は，

 I ＝ dQ  ＝ S dD
dt dt

となります。 もちろんこれは変位電流 I に等しい値です。この両辺 S で割って，ベクトル表記すれば，

  j　＝  I   ＝ ∂D
 S ∂t

これを変位電流密度といいます。

［２］　また，D ＝ ε0E ＋P  より[#]，コンデンサーの電極間が真空のときの寄与と物質の寄与を分離すると，

 j　＝ ∂D ＝ ∂ε0E  ＋ jp　　　；  ただし，　j p ＝ ∂P
∂t ∂t ∂t

ここで，物質が挿入されたことによる寄与　j p を分極電流密度と呼びます。

［３］　一方，充電によってコンデンサーの両電極に正負の対電荷±Q0を形成するために必要なエネルギーは次のように計算されます。(09/06/20)

U＝ Q0 VdQ＝ Q0 Q dQ＝ Q02
0 0 C0 2C0
　　＝ 1 C0V2 ＝ ε0S (Ed)2
2 2d
　　＝ 1 ε0(Sd)E2
2

ここで，このページ冒頭の(1)-(3)を用いており，電極の間には均一な電場E が形成されているとしています。さらに(Sd)が電場の存在する電極間の体積であることを考慮すると，

u≡ U ＝ 1 ε0E2   静電エネルギー密度 
Sd 2

を定義し，これを電場Eのもつ単位体積あたりの静電エネルギー密度と解釈することができます。この解釈は一様でない一般的な電場にも拡張することができます。(証明は別に必要)

以上ですが，このページでやったことは，電磁気学(工学)で使われる専門用語の定義とその解説であって，新しい法則については何も述べていません。前ページまでも含めてここまでに提示された電磁気学の原理は，「クーロンの法則」 だけです。「ガウスの法則」 というのも出てきましたが，これはクーロンの法則の数学的な言い換えに過ぎません。
電磁気学における第２の原理を次のページで述べる「ローレンツ変換則」 として導入します。

［ 目次へ ］