| 7 ローレンツ変換 | ||
| f-denshi.com [目次へ] 最終更新日: 24/04/18 | ||
| サイト検索 | ||
ローレンツ変換とは電磁気学の法則(マクスウェルの方程式)をすべての慣性系で不変に保つような座標変換はどうあるべきかという考察に基づいて,ローレンツが初めて提案しました。後にアインシュタインはこれを,「光速度不変の原理」 と呼ばれる時間・空間のもつ基本的な性質であることを提唱し,力学にも適用して現在,特殊相対性理論として知られる体系を作り上げました。本ページではローレンツ変換を光速度不変の原理から導き,その解釈を簡潔に述べます。特殊相対性理論は,それだけの説明で一冊の本が書ける内容を含んでいます。しかし,本講義は相対性理論の解説を目的とはしておらず,ローレンツ変換はあくまで,電磁気学体系の中での第2番目の”公理”として位置づけています。したがって,結果[#]だけをそのまま受け入れて,先へ読み進んでも構いません。
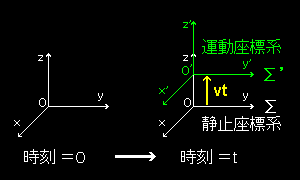
[1] 互いに等速直線運動する2つの座標系を考えます。ひとつは静止座標系と呼ぶ座標系
Σ(x,y,z) です。もうひとつは静止座標系から見てz 軸の正方向へ速度v で運動している座標系 Σ '(x',y',z') で運動座標系と呼ぶことにします。
時刻 t=0 で,2つの座標系ΣとΣ 'の座標軸が完全に一致しているとすると,任意の時刻 t=t でのΣ ' の原点はΣの座標で,(0,0,vt) に見出すことができます。
[2] さて,光が時刻 t = 0 で全方向に向かって放たれて広がってゆく様子をこの2つの座標系で観測したとします。このとき,光はすべての座標系(観測者)において速度 c で進むこととします。 (=光速度不変の原理 ← 実験事実!で電磁気学の2つ目の原理です。[#])
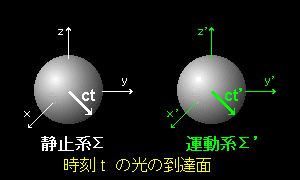
すると,t 秒後の光の到達面はどちらの座標系でも半径 ct の球面上にあるはずです。ただし,時刻 t は2つの座標系で同じとは限りらないとします。そこで,運動座標系の時刻には t'という記号を使いましょう。すると,その球面の方程式は,
x2 +y2 +z2 =(ct)2 ・・・・・・・・・・(1)
x'2+y'2+z'2=(ct')2 ・・・・・・・・・・(2)
となります。これを満たすように静止座標系Σ(t,x,y,z) と運動座標系Σ '(t,x',y',z') との”関係” = ”座標変換の式” を求めることがここでの問題です。
[3] 2つの座標系は対等でなければいけないことと,x,y方向の空間対称性を考慮すれば,座標変換は1次変換:
A,B,δ,γ は適当な定数
t' = At+Bz
x' = x
y' = y
z' = δt+γz・・・・(3)
とおくことは妥当でしょう。
(要するに,縦ベクトル x = t(t,x,y,z),y = t(t,x',y',z')を考えて,これらが座標変換の行列P で,y = Px,x = P-1y と関係付けられるということ。 ただし,P-1はP の逆行列で,P の成分に含まれる,v を -v と置き換えて得られるようでなければいけません。)
さらに座標系Σ 'の空間原点(0,0,0)の運動を観測した場合,Σ 'では時間によらず,(x',y',z') = (0,0,0)ですが,Σでは(x,y,z) = (0,0,vt) となるので,((3)の第4番目の式 0 = δt+γzより) z = -δt/γ = vt でなければなりません。逆にΣ 'から見たΣの位置座標の原点を観測した場合,(x,y,z) = (0,0,0) に対して,(x',y',z') = (0,0,-vt),すなわち,z' = δt = δt'/A = -vt' ,(←(3)の第4番目と1番目 t'= At+B ・ 0 を使ってます。)つまり,
δ = −γv
A = γ
が成り立つ必要があります。したがって,(3)の1行目,4行目の式は,
t'= γt+Bz
z'= γ(−vt+z)・・・・(4)
と書けます。
[4] 次に,(4)を(2)に代入して,整理すると,
x2+y2+(γ2−c2B2)z2 = (c2−v2)γ2t2 + 2(vγ+c2B)γzt ・・・・ (2)’
これを(1)に等しいとおいて解けば,
γ2−c2B2 = 1
(c2−v2)γ2 = c2
vγ+c2B = 0
これを解くと,
γ= 1 , B=− v ・・・ (5)
1−(v/c)2
c2 1−(v/c)2
となります。記号を改めて,
ローレンツ変換
ここで,
|
||||||||||||||||||||||||||||||||||
ローレンツ変換を行列で表すと次のような線形変換であることが分かります。
ct’ = γ 0 0 -γβ ct ・・・ (6) x’1 0 1 0 0 x y’2 0 0 1 0 y z’3 -γβ 0 0 γ z
ローレンツ変換 L=(Lij ) の逆行列は,
L-1=((L-1)ij )= γ 0 0 γβ ・・・ (7) 0 1 0 0 0 0 1 0 γβ 0 0 γ
[1] 長さ
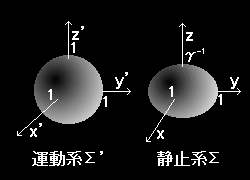
運動座標系Σ ' で静止している半径 1 の球
x'2+y'2+z'2 = 1 [ 球面の方程式 ]
は静止座標系 Σ から見ると,座標変換: x' =x,y' =y,z'=γ(z−vt) より
x2+y2+ (z−vt)2 = 1 [ 楕円面の方程式 ] (1/γ)2
(↑時刻とともに中心は移動します。)
なので,
運動している物体は静止系から見ると,運動方向に γ 分の 1 に収縮して見える。
これをローレンツ収縮といいます。もちろん,電荷を帯びている物体についてもこの収縮は観察されます。一方,電荷保存の法則から電荷はどちらの座標系でも等量だけ存在するので,結局これは,
「座標系によって電荷密度が違って見える」 ことを意味するのです!
[2] 時間
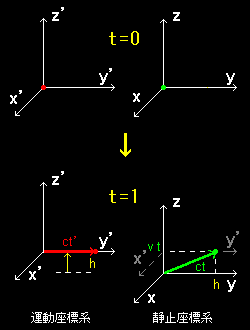 運動座標系において時刻 0 に発した光が y' 軸正方向にまっすぐ進み, t'
秒後に,
運動座標系において時刻 0 に発した光が y' 軸正方向にまっすぐ進み, t'
秒後に,
y' = h = ct'
に到達したとします。一方,これを静止座標系で観察すると,光はy 軸方向へ
y = h = ct
進むだけでなく,z 軸方向へも vt だけ進んでいるはずです。すると,三平方の定理から,
(ct)2 = (ct')2 + (vt)2
が成立しなければなりません。書き直すと,
t’ =
1−(v/c)2 = 1 < 1 t γ
つまり,
運動座標系の時計は静止座標系から見ると γ 分の 1 のスピードでゆっくり進む。
(2024/04/18 加筆)
[1] 粒子の運動を記述するために時刻 (c をかけて長さの次元とする) と位置,
x0=ct, x1=x, x2=y, x3=z ←肩の数字は成分を表す指標
の4つの成分をもつ4次元空間を考えます。この空間の点は世界点と呼びます。
さらにこの空間を計量ベクトル空間 [#] にするために,(ミンコフスキー)計量テンソル [#] を次のように定義します。
η=ηij=ηij= -1 0 0 0 ・・・ (1) 0 1 0 0 0 0 1 0 0 0 0 1
これはこの空間の2つの世界点の距離 ds の2乗を
(ds)2≡−(dx0)2+(dx1)2+(dx2)2+(dx3)2 [世界距離の2乗]
で与えることに相当します。
[2] なぜ,このように距離を入れるのかといえば,座標系Σからローレンツ変換によって座標系Σ’へ移行した場合に,
−(dx0)2+(dx1)2+(dx2)2+(dx3)2 =− (dx'0)2+(dx'1)2+(dx'2)2+(dx'3)2
・・・ [*]
が成立するからです。つまり,ローレンツ変換に対して不変量となるからです。
特に光の球面波を原点からの距離として観測した場合,この等式は,1.で調べたように
(ct)2 +x2 +y2 +z2 = 0 =−(ct')2+x'2+y'2+z'2
という式に対応します。
一般的には,座標系Σで,
点P=( (x0)p, (x1)p,(x2)p,(x3)p ), 点Q=( (x0)q ,(x1)q ,(x2)q ,(x3)q )
ローレンツ変換後の座標系Σ’では,
点P=( (x'0)p, (x'1)p,(x'2)p,(x'3)p ), 点Q=( (x'0)q ,(x'1)q ,(x'2)q,(x'3)q )
として,ローレンツ変換
x’0 = γ 0 0 -γβ x0 x’1 0 1 0 0 x1 x’2 0 0 1 0 x2 x’3 -γβ 0 0 γ x3
をP,Qの各点についておこなってみると,
− (dx'0)2+(dx'1)2+(dx'2)2+(dx'3)2
=− ((x'0)p-(x'0)q )2+( (x'1)p-(x'1)q)2+((x'2)p-(x'2)q)2+((x'3)p-(x'3)q)2
=−(γ((x0)p-(x0)q)−γβ((x3)p-(x3)q))2+((x1)p-(x1)q)2+((x2)p-(x2)q)2
+(−γβ((x0)p-(x0)q)+γ((x3)p-(x3)q))2
=− ((x0)p- (x0)q )2+((x1)p-(x1)q)2+((x2)p-(x2)q)2+((x3)p-(x3)q)2
=−(dx0)2+(dx1)2+(dx2)2+(dx3)2
のように確かめることができます。
[3] そこで,固有時と呼ばれるτ を用いて,
(cdτ)2 ≡ (cdt)2−(dx)2−(dy)2−(dz)2 (=-(ds)2) ・・・[**]
とおくことにします。粒子の速度が光速より遅ければ,世界距離の2乗 (ds)2 は負の値をとるので,(cdτ)2>0 となり,dτは実数値をとります。このような条件を満たすことを時間的領域にあるともいいます。
このτが固有時と呼ばれる理由は,ある座標系Σを静止座標系,等速運動する粒子に固定された運動座標系をΣ’とすれば,Σ’において粒子は静止しているので,時間変化があっても
dx'=dy'=dz'=0
であるから,[*]と[**]より,
(cdτ)2= (cdt')2 ⇒ dτ=dt'
すなわち,dτはそれぞれの運動粒子に固定された時計の刻み,つまり,τは運動粒子固有の時刻を示しているからです。そして,特殊相対性理論では,運動粒子の記述(物理法則)はこの固有時を使って行われなければならないとするのです。
言い換えれば,運動粒子を観測する慣性系(このページでは静止座標系と呼んでいる)の時計を用いるこはできないということです。
[4] さて,[**] を c2 で割ると,
dτ2 =dt2 1− dx 2 + dy 2 + dz 2 cdt cdt cdt
さらに平方根をとって,プラス符号を選択すれば,
dτ= dt ・・・ (2) γ ただし,
γ= 1
1−(v/c)2 ,
v2= dx 2 + dy 2 + dz 2 dt dt dt
という関係式が得られます。γは v << c のときは 1,光速度 c に近づくにつれて +∞ となります。
つまり,運動粒子の時計の時刻τはその速度が速いほど,それを観測する静止系Σの時計の時刻 t に比べてゆっくり進み,光速になると止まってしまうということです。
[5] さらに,特殊相対性理論で用いられる用語の説明を続けると,長さの単位をもつ,4元位置ベクトル (ct,x,y,z) をτで微分したベクトルを粒子の4元速度 ui と定義します。
u ≡ dxi = cdt , dx , dy , dz = γc,γ dx ,γ dy ,γ dz ・・・ (3) dτ dτ dτ dτ dτ dt dt dt
すなわち,
u =(u0,u1,u2,u3)=(γc,γvx,γvy,γvz) [4元速度]
=γ(c,vx,vy,vz)
ただし,
vx= dx ,vy= dy ,vz= dz dt dt dt
を定義します。
速度が光速より十分小さいときには,γ = 1 と近似できて,
(u1,u2,u3) ⇒ (vx,vy,vz)≡v古
すなわち,4元速度の第2から第4成分はニュートン力学における速度と一致します。
[6] さらに粒子の(静止)質量mを4元速度に乗じた4元運動量 pi≡mui ,すなわち,
p =(p0,p1,p2,p3)=m (u0,u1,u2,u3) [4元運動量]
=(γmc,γmvx,γmvy,γmvz)
=γ(mc,px,py,pz)
( = (E/c,p) )
を定義します。ここで,(px,py,pz)≡(mvx,mvy,mvz)≡p古 はニュートン力学における運動量成分です。
4元運動量の第2〜4成分 p1,p2,p3 は速度が光速より十分小さいときに,γ = 1 と近似して,
p≡ (p1,p2,p3) ⇒ (px,py,pz) =p古 ・・・ (4)
とニュートン力学における運動量と一致することが分かります。
[7] 一方,4 元運動量の第1成分は,それに光速度 c を乗じたcp0 =γmc2 を物体の(相対論的) エネルギー E と定義します。
E ≡ cp0 = γmc2 ・・・ (5)
この量は,光速度より十分小さな速度で運動するときには,古典力学の運動エネルギーに関連付けられることを次のように示すことができます。
まず,[**]式に(mγ)2を乗じて,(dt)2で割ると,
| (mγ)2 | c | dτ | 2 | =(mγ)2c2−(mγ)2(dx/dt)2−(mγ)2(dy/dt)2−(mγ)2(dz/dt)2 | ||
| dt |
↑ ↓ γdτ=dt より
(mc)2 = (γmc)2−(γmvx)2−(γmvy)2−(γmvz)2 ・・ (6)
と変形します。すると,この結果を4元運動量 pi を用いて表せば,
(mc)2 = (p0)2−(p1)2−(p2)2−(p3)2
= (p0)2−p2 ・・・ (7)
さらに,(7)式の両辺に c2 をかけると,E と mc2 の関係式を得ます。
(mc2)2=E2−(pc)2 [***]
そして,速度vが光速度cに比べて十分小さいとして,
E =
(mc2)2+(pc)2
=mc2
1+ (cp)2 (mc2)2
≒mc2 1+ (cmv)2 2 (mc)2
=mc2+ mv2 =mc2+ px2+py2+pz2 ・・・ (8) 2 2m
となります。 ここで,第2項, mv2/2 はニュートン力学における運動エネルギー E古 です。
一方,第1項 mc2 は,第2項がゼロ,すなわち,静止座標系Σにおいて物体が静止しているときに持つエネルギーと考えることができるので,静止エネルギーと呼ばれます。つまり,相対論的な運動する粒子のエネルギーとは,「静止エネルギーと運動エネルギーの和である」 と近似的に考えることができます。
[8] 次に力ですが,p=(p0,p1,p2,p3)=m (u0,u1,u2,u3) と
ニュートン力学の運動量と力の関係,
F古≡ dp古 ・・・・・ (9) dt
を念頭において,時間 t をτ,運動量を4元運動量 p=(p0,p1,p2,p3)=m (u0,u1,u2,u3) とすることで,4元力 f =( f0,f1,f2,f3) を次のように定義します。
f ≡ dp = dp0 , dp1 , dp2 , dp3 =m d2u0 , d2u1 , d2u2 , d2u3 [4元力] dτ dτ dτ dτ dτ dτ2 dτ2 dτ2 dτ2
これもローレンツ不変量です。
当然ながら,v << c で,γ=1とみなせるときは,第2〜第4成分(空間成分)は古典力学の関係式 (9) に帰着されることが確かめられます。すなわち,
f古≡ dp = dp ・ dτ = dp γ-1=fγ-1 dt dτ dt dτ
f =(f1,f2,f3)=γf古
と定義すると,γ→1 のとき,
dp ⇒ dp古 =F古 ,および, f ⇒ f古 dt dt
なので,
f ⇒F古
ということです。