エチレン分子の分子軌道
f-denshi.com  更新日：

π−π電子の相互作用による分子軌道の形成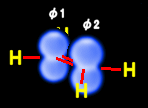

エチレンの２重結合はC-C間の結合として，sp2結合とそれと垂直方向に広がるπ-π結合との２つの結合からできています。
ここでは，π-π相互作用による

・シュレーディンガー方程式を

Hψ ＝ Eψ                ・・・・・・・・・・・・・・・・・・・・・   （１）

・分子軌道：　ψ＝原子波動関数 φ1，φ2 の１次結合として，

ψ ＝ λ1φ1＋λ2φ2　　，　（ ψ* ＝ λ*1φ*1＋λ*2φ*2 ）          ・・・・・・・・・   （２）

・エネルギーは，

E ＝ ψHψ* dV                            ・・・・・・・・・・・・・・・・・・・・・・   （３）
ψ*ψdV

ここで，分母はψが規格化されていれば１ですが，あえてこのように書いておきます，次に記号の置き換えをします。

（３）の分母 ＝ λ1λ*1φ1φ*1＋λ1λ*2φ1φ*2 ＋λ*1λ2φ2φ*1 ＋λ2λ*2φ2φ*2 ｝dV
   　　　　＝λ1λ*1 φ1φ*1dV ＋λ*1λ2 φ*1φ2dV＋λ1λ*2 φ*2φ1dV  ＋λ2λ2 φ2φ*2dV
            ＝λ1λ*1S11＋λ*1λ2 S12 ＋ λ1λ*2S21 ＋λ2λ*2S22　
            ＝λ12 ＋λ22　＋λ*1λ2 S12 ＋ λ1λ*2S21 　　

［２］　ここで，

S11 ≡ φ1*φ1 dV ＝ 1，    S22 ≡ φ2*φ2 dV  ＝ 1       原子波動関数の規格化より

を用いてます。 また，分母は規格化条件から 1 に等しいので，

ψ*ψdV ＝ λ12 ＋λ22　＋λ*1λ2 S12 ＋ λ1λ*2S21 ＝ 1　　　［拘束条件］　　　･････････　[*]  

を満たさなければいけません。

［３］　一方，分子 I は，

α ＝ H11≡ φ1*Hφ1 dV  ＝ H22 ≡ φ2*Hφ2 dV
β ＝ H12≡ φ1*Hφ2 dV ＝ H21 ＝ φ2*Hφ1 dV

という記号で置き換えれば，

（３）の分子 ＝ λ*1λ1φ*1Hφ1＋λ*1λ2φ1*Hφ2 ＋λ1λ*2φ2*Hφ1 ＋λ*2λ2φ2*Hφ2 ｝dV
           ＝λ12α ＋ （λ*1λ2 ＋λ1λ*2）β ＋ λ22α          　　　　　　　　･････････････････　[**]

これらを（１）に代入すれば，

E ＝ ψHψ* dV ＝ λ12α ＋ （λ*1λ2 ＋λ1λ*2）β ＋ λ22α  
ψ*ψdV
λ12 ＋λ22　＋λ*1λ2 S12 ＋ λ1λ*2S21

この Ｅ がλ1 ，λ2 の関数として極値をとるための必要条件は，

∂E  ＝ ∂E   ＝ ∂E  ＝ ∂E  ＝　0
∂λ1 ∂λ2 ∂λ*1 ∂λ*2

ただし拘束条件を忘れてはいけません。そこで，

（λ12 ＋λ22 ＋λ*1λ2 S12 ＋ λ1λ*2S21）E 
                            ＝ λ12α ＋ （λ*1λ2 ＋λ1λ*2）β ＋ λ22α      　･････････････････　[***]

の偏微分をとると [#] ，

（λ*1＋λ*2S21）E ＋（λ12 ＋λ22＋λ*1λ2 S12 ＋λ1λ*2S21） ∂E ＝　λ*1α ＋ λ*2β　　　
∂λ1
（λ*2＋λ*1S12 ）E ＋（λ12 ＋λ22＋λ*1λ2 S12 ＋λ1λ*2S21） ∂E ＝　λ*1β　＋λ*2α　
∂λ2
（λ1＋λ2S12 ）E ＋（λ12 ＋λ22＋λ*1λ2 S12 ＋λ1λ*2S21） ∂E ＝　λ1α ＋ λ2β　　　
∂λ*1
（λ2＋λ1S21）E ＋ （λ12 ＋λ22＋λ*1λ2 S12 ＋λ1λ*2S21） ∂E ＝　λ*1β　＋λ*2α　
∂λ*2

これより，E，α，βが実数値であることに注意すれば，

（λ1＋λ2S12）E  ＝　λ1α ＋ λ2β
（λ2＋λ1S21）E  ＝　λ2α ＋ λ1β

が停留条件。さらにこれは，λ1，λ2 に関する連立１次方程式であって，行列とベクトルを用いてあらわすと，

α−E β−S12E λ1 ＝ 0
β−S21E  α−E λ2 0

［］　さらに近似として，

S12 ≡ φ*1φ2 dV ＝0，　　S21 ≡ φ*2φ1 dV ＝ 0　　　　   ［ 重なり積分 ＝ 0 ］

も用いると，

α−E β λ1 ＝ 0
β α−E λ2 0

これが自明な解 λ1＝λ2＝0  以外の解を持つ条件として，

　 α − E β 　 ＝ 0
β α − E

が得られます。これを解くと，

E  ＝α±β，　　
λ1 ＝
1
2
　　複合同順
λ2
±
1
2

となります。





［目次へ］

λ1，λ2 が複素数であることの注意