
| 2 巡回群(平面内の回転群) |  |
|
| f-denshi.com 最終更新日: 04/02/27 | ||
| [目次へ] | ||
| サイト検索 | ||
この章では変換群として平面回転群を例に挙げ,群論に用いられる基本用語を説明します。
[1] 正六角形の重心O の回りに 0°,60°,120°,180°,240°,300° それぞれ平面内で正方向(反時計周りに)回転した場合,正六角形の位置は見かけ上変わりません。この回転操作(写像)をそれぞれ順番に,e,g1,g2,g3,g4,g5 と書き,その全体の集合をR6としましょう。 すなわち,集合
R6={e,g1,g2,g3,g4,g5}
は6個の元からなり,各元の意味を図示すると,図1のようになります。
|
|
図1 巡回群R6の6つの元
[2] 次に,この集合の任意の2つ元の間に積と呼ばれる演算 ・ をこれら回転操作を2回続けて行うこと(合成写像)として定義します。たとえば,
g1・g2=g3
とは,
「最初に g2(120°の回転),次に g1(60°の回転)を行うことは g3(180°の回転)を行うことに等しい」
ことを意味します。すると,集合R6は積 ・ について群をなします。この集合の任意の2つの元の積は再びこの集合に属し,単位元は恒等写像 e ,また,gi (i=1,2,3,4,5)の逆元は g6-i であり,eの逆元はe自身であることは容易に確かめられます。演算結果を一覧表にすると次のようになり,群表と呼ばれます。
gi・gj e g1 g2 g3 g4 g5 e e g1 g2 g3 g4 g5 g1 g1 g2 g3 g4 g5 e g2 g2 g3 g4 g5 e g1 g3 g3 g4 g5 e g1 g2 g4 g4 g5 e g1 g2 g3 g5 g5 e g1 g2 g3 g4
表1 正六角形の平面回転群(=Z6)の群表
[3] 上と同様に正n角形について平面回転群を定義できます。このような平面回転群を巡回群と総称し,Znという記号を使います。この慣習に従い,これからは
R6 ⇒ Z6
と書くことにしましょう。
これから巡回群 Z6 を例に取って群論に使われる基本用語を解説していきたいと思います。
[1] 群 G の元の個数を群Gの位数と呼び,|G|と書きます。上の例の群 Z6 の元の個数は6個なので,
|Z6|=6
と書きます。このように位数が有限個の場合を有限群といいます。一方,整数の集合に普通のたし算,+ を演算規則とする群では元の個数が無限にあり,このような群は無限群といいます。
[2] さて,Z6 は6個の元のひとつ,g1 については,自分自身との積(演算)を繰り返すことで,
(g1)2 = g1・g1 =g2,
(g1)3 = g1・g1・g1 =g3,
(g1)4 = g1・g1・g1・g1 =g4,
(g1)5 = g1・g1・g1・g1・g1 =g5,
(g1)6 = g1・g1・g1・g1・g1・g1 = e
となり,G のすべての元 e,g1,g2,g3,g4,g5 が作り出されます。このような元を群Gの生成元といい,
G = <g1>
と書きます。すべての元が生成元になるわけではありません。各元をn乗した値の一覧表をつくると,
(gi)n乗 2乗 3乗 4乗 5乗 6乗 e e e e e e g1 g2 g3 g4 g5 e g2 g4 e g2 g4 e g3 e g3 e g3 e g4 g2 e g4 g2 e g5 g4 g3 g2 g1 e
表2 群Z6のn乗表
となり,g1と g5 だけが群 Z6 の生成元であることがわかります。また,群によっては,生成元は一つではなく2つ以上の元,例えば,3つの元,a,b,c から構成されている場合もあり,G =<a,b,c> のように書きます。たとえば⇒2面体群[#]
[3] つぎに,上の表で,g2 の行について見てみますと,
(g2)2=g4,
(g2)3=e
となり,これ以上 g2 との積を繰り返しても,g2,g4,e以外の元は現れないことに気づきます。g3 に関しても,同様です。有限群の場合はどの元 a も必ず,ある k が存在して,
(a)k=e
となりますが,この k のうち最小のものを元 a の位数といいます。(←群Gの位数[#]とはまったく別ものです。注意!) 上の群表から,R6 の各元の位数は,
元 a = e g1 g2 g3 g4 g5 元の位数 k = 1 6 3 2 3 6
となります。ここで位数 1,2,3,6 は必ず6の約数となっていますが,これは有限群について,
| 定理 有限群 G の元 g の位数 k は群 G の位数|G|の約数である。⇔ |G|=ks : s は整数 |
ことが成り立つためです[証明略]。
[4] 特に,群 G の位数|G|が素数のときは1とそれ自身しか約数をもちません。ということで,次の定理が成り立ちます。
| 定理 群 G の位数が素数 p であるならば, (1) 単位元を除く,すべての ”元の位数” は p である。 |
注意すべきことは,この定理(2)の逆は成り立ちません。実際,R6は|G|=6 (偶数⇒素数でない)ですが,巡回群となっています。
(2)の証明は一番最後で → [#]
[5] さらに,a|G|=aks=(ak)s=(e)s=e なので,(元aの位数をkとして)
| 命題 群 G の任意の元 a に対して, a|G|=e |
が成り立ちます。これは表2で,すべての元が6乗すると e になることに対応しています。
[6] 巡回群の場合,ある生成元をγとして一つ固定すれば,G の任意の元 g は,g = γm (1≦m≦n=巡回群の位数)
として,一意的に書けます。つまり,γ を固定すれば,G の任意の元と整数 m とが1対1で対応します。この m のことをg のγに関する指数といい,
indγ(g)=m
と書きます。例えば,巡回群Z6を例にとれば,生成元 g5 を用いて,
indg5(g1)=5, ⇔ (g5)5=g1
indg5(g2)=4, ⇔ (g5)4=g2
indg5(g3)=3, ⇔ (g5)3=g3
indg5(g4)=2, ⇔ (g5)2=g4
indg5(g5)=1,
となります。また,indg5(e)=6 ですが,約束としてすべての生成元γ自身については
indγ(e)=0
と定義します。このように定義すると普通の実数を扱うときの指数法則と同様な規則が成り立ち便利なのです。
[7] Z6 = {e,g1,g2,g3,g4,g5} は,代数方程式: X6=1 の解の集合:
ωk =e2πki /6 =cos(kπ/3)+isin(kπ/3); (k=0,1,2,3,4,5)
と1対1の対応が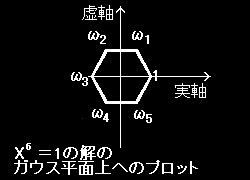 あります。
あります。
| Z6 | e | g1 | g2 | g3 | g4 | g5 |
| (g1)0 | g1 | (g1)2 | (g1)3 | (g1)4 | (g1)5 | |
| ωk= | 1 | ω1 | ω2 | ω3 | ω4 | ω5 |
| (ω1)0 | ω1 | (ω1)2 | (ω1)3 | (ω1)4 | (ω1)5 |
これは容易に一般化でき,Xn=1 の解の集合は位数 n の巡回群をなし,
ω1=e2πi /n のベキであらわすことができます。
参考 → [#]
[1] さて,Z6 から3つの元 g2,g4,e どうしの積の結果を表1から抜き出してみると,
gi・gj e g2 g4 e e g2 g4 g2 g2 g4 e g4 g4 e g2 ⇔
ti・tj e t1 t2 e e t1 t2 t1 t1 t2 e t2 t2 e t1 表2 部分群 H1/3 3文字の巡回群 Z3
となり,Z6 の部分集合: H1/3={e,g2,g4} も 3つの元からなる群になっていることがわかります。このように群 G の一部の元を抜き出した部分集合 H が,もとの群 G と同じ演算のもとで,やはり群になっているとき,それをG の部分群といいます。この例では,部分群 H1/3 は,g2を生成元とする巡回群でもあるので,巡回部分群ともいいます。H1/3 の単位元以外の元は,
(g2)2=g4, (g2)3=e
(g4)2=g2, (g4)3=e
なので,H1/3 は e と元の位数3の元から成り立っていることがわかります。この群は位数3の巡回群 Z3 と同じ構造を持っていることにも注意してください。
さらに,H1/2 = {e,g3} も Z6 の巡回部分群となってます。
gi・gj e g3 e e g3 g3 g3 e ⇔
ri・rj e r e e r r r e 表3 部分群H1/2 巡回群 Z2
g3 に関しては,
(g3)2 = e
なので,g3 の位数は2であることに注意してください。このように一つの群に対して部分群は複数個存在することができます。
[2] 部分群に関して重要な性質を挙げておきます。
|
命題 (1) x,y ∈ H ならば,xy ∈ H かつ,x-1 ∈ H |
これはある集合が部分群であることを証明するときによく使われます。
(1)の証明 略
(2)の証明
Gの部分集合 H が条件(2)を満たしていれば,
・ y=x とおけば,x-1x=e ∈ H ⇒ 単位元 e は H に含まれる。
・(2)で y=e とおけば,x-1e =x-1 ∈ H
⇒ x∈H の逆元 x-1は H に含まれる,
・HはGの部分集合なので,Gの元とみなして結合法則が成り立つ。
すなわ,部分集合Hは群Gの演算の下で群の定義をみたす。
逆にHがGの部分群であるならば,(2)を満たすことは明らか。(終)
さらに,
| 定理 有限群 G の部分群Hの位数|H|は群 G の位数|G|の約数である。 |
が成り立っています[証明略]。今の場合,
|Z6|=6 に対して,部分群では,|H1/3|=3,|H1/2|=2
なお,この定理の逆は成り立ちませんが次の定理が知られています。
[3] 最後に群 G とその部分群 H との位数に関する重要な関係:「シローの定理」を証明抜きに紹介しておきましょう。)
| シローの定理(第一定理) 群 G の位数が, |G|= p1s×p2t×・・・×pnw と一意的に素因数分解できるとき,位数が,p1s,p2t,・・・,pnw の部分群がそれぞれ少なくとも一つは存在する。 |
位数6の巡回群Z6の例では,
6=21×31
なので,位数が2 および,3の部分群がそれぞれ一つは存在することをこの定理は述べています。この定理は
「 |G|を割る 素数 p の最高ベキ数 pr を位数とする G の部分群の存在 」
を保証しているということもできます。この位数 pr の部分群を群 G の p-シロー群 といいます。
[4] ただし,次の二つのことを注意しておきましょう。
(1)この定理は群 G の部分群が p-シロー群に限ることをいっているのではない。
(2)一つのprに対応して1つの部分群しか存在しないといっているものではない。
正四面体群のところでも,具体例をみることができます。[#]
証明:
任意の位数 n の巡回群 Z とは,
「位数 n の元 ω1 が存在して,Z のすべての元を{e,ω1,(ω1)2,・・・・,(ω1)n-1}と表すことができる群 」
と言い換えることができます。
一方,「 有限群 G の元 の位数 は群 G の位数|G|の約数でなければならない」 ので,もし,群 G の位数 p (≠1)が素数ならば,群 G のすべての元の位数は 1 か p である。したがって,G には,位数 p の元 g が存在して,
g,g2,・・・・,gp-1,gp=e
のp 個の元で G の元は尽くされる。つまり,G は巡回群である。
|
命題
|