
| 10-1 中心と中心化群 |  |
|
| f-denshi.com 更新日: 21/03/25 群表をたくさん追加しました。 | ||
| [目次へ] | ||
| サイト検索 | ||
急ぐ方はこの章を飛ばして「11」へ進んでも構いません。
このページは正規部分群を見つけ出すツールの紹介です。
[1] しばらく抽象的な定義を列挙しますが,すぐわからなくてもそのまま読み進み,そのあとにあげる具体例をみながら,行きつ戻りつしてください。
| 定義 G の中心 群 G のすべての元と可換な G の元全体は G の(正規)部分群となる。この部分群を G の中心 Z (G) という。 Z (G)={h|hg = gh ; すべての g∈G } |
中心とは共役[#]の条件をさらに厳しくしたものと見ることができます。つまり,h と a が共役であるというときの g の条件は,”ある g∈G” だったのですが,中心では, ”すべての g∈G” となっているところに注意してください。また,
| 命題1 (1) 可換群 G の中心は G 自身である。 (2) 群G の中心 Z (G)の部分群はすべてG の正規部分群である。← この逆は成り立たない |
[証明] ⇒ [#]
[2] さらに,G の G自身への働きを考えたときの固定部分群[#]には特別な名称がついてます。
| 定義 a∈G の中心化群 群 G の G自身への両側からの働きを考えるとき,a∈G の固定部分群 Ca を 「a の中心化群」 という。 言い換えると,a∈G と可換な G の元全体の集合, Ca ={ g|ga=ag ; g∈G } ={ g∈G|gag-1=a } を 「 a の中心化群」 と呼ぶ。 |
この用語を用いれば,中心 [#] とは中心化群 Ca=G ( a と可換な元全体の集合がGと一致)[#]となる a を集めてきたものなのです。
[3] このとき,次の定理が成り立ちます。
| 定理1 群 G の元 a の共役類 C(a)の位数|C(a)|と a の中心化群の位数|Ca|との関係は, |G|=|C(a)|×|Ca| |
[証明]
これは,7.類別2 で述べた固定部分群と剰余類の軌道に関する定理の(3)[#]において,G-軌道を共役類,固定部分群を中心化群としたものです。(つまり,Gの働く相手Mを頂点ではなく,G自身とする。)
正四面体群について確かめてみると,共役類は,
C(ak)={a1,a2,a3,a4}
C(bk)={b1,b2,b3,b4}; k = 1,2,3,4
C(hj)={ hx,hy,hz} ; j = x,y,z
C(e) ={e}
一方,中心化群は,
Cak=Cbk={e,ak,bk}
Chj={e,hx,hy,hz}
Ce= G
であるから,
|C(ak)|×|Cak|=4×3=12
|C(hj)|×|Chj|=3×4=12
|C(e)|×|Ce|=12×1=12
などが確かめられます。
以上の定義,定理について例でその意味することを確認して行きましょう。
まず,これまで調べてきた正四面体群の中心は,単位元 { e } だけです。この e について上記の定理などを具体的に確かめることができますが,これでは簡単に過ぎるので,ここでは他の例として単位元以外にも中心を持つ,結晶点群で C4v または,4mm と呼ばれる群を調べて見ましょう。
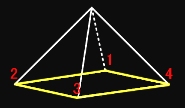
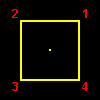
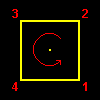
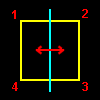
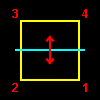
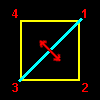
[4] C4v は,いわゆるピラミッドの3次元空間内での広義の回転対称操作を取り出した群です。その元の名称と対応する操作は下図のように正方形の底面の4つの頂点の動きで分類することができます。
ここで,σj というのは鏡映対称と呼ばれる変換で,下図の水色の線上に鏡をこの(モニタの)画面に垂直において鏡写ししたものとなります。その群表は下のようになります。
 |
|||
 |
 |
 |
 |
| e | c1 | c2 | c3 |
 |
 |
 |
 |
| σx | σy | σd | σd’ |
| X・Y | e | c1 | c2 | c3 | σx | σy | σd | σd’ |
| e | e | c1 | c2 | c3 | σx | σy | σd | σd’ |
| c1 | c1 | c2 | c3 | e | σd’ | σd | σx | σy |
| c2 | c2 | c3 | e | c1 | σy | σx | σd’ | σd |
| c3 | c3 | e | c1 | c2 | σd | σd’ | σy | σx |
| σx | σx | σd | σy | σd’ | e | c2 | c1 | c3 |
| σy | σy | σd’ | σx | σd | c2 | e | c3 | c1 |
| σd | σd | σy | σd’ | σx | c3 | c1 | e | c2 |
| σd’ | σd’ | σx | σd | σy | c1 | c3 | c2 | e |
[5] 背景が白い部分を見ると,c2 はすべての元,g∈C4v と可換であることがわかります。(元の幾何学的な意味は右図を見よ)このような元は他には単位元 e しかありません。したがって,
(1) 群 C4v の中心 [#] は,部分群:Z (C4v)={e,c2 } となります。
X・Y e c2 e e c2 c2 c2 e
(2) これ以外にも自明でない部分群としては,
{e,σx },{e,σy },
{e,σd },{e,σd’},
{e,c1,c2,c3 },{e,c2,σx,σy},{e,c2,σd,σd’}
が存在します。
(3) 共役類 [#] は,
{e},{c2},{c1,c3},{σx,σy},{σd,σd’}
であって,C4v は5つの共役類に分割されています。
[6] たとえば,c1,c3 が共役 [#]であることは次のような計算結果から,
g= e c1 c2 c3 σx σy σd σd’ g-1= e c3 c2 c1 σx σy σd σd’ g・c1g-1= c1 c1 c1 c1 c3 c3 c3 c3 g・c3g-1= c3 c3 c3 c3 c1 c1 c1 c1
わかります。つまり,
C(c1)={ c1,c3 } ←左右の90°回転は同じ仲間
また,共役類は共通部分がない同値類に分類されているので,
|C4v|= |C(a)|
この関係式は類等式と呼ばれます。
(4) c1 の中心化群: Cc1={ g|g・c1=c1・g; g∈G }は c1 と可換な元を抜き出して,
Cc1={ e,c1,c2,c3 }
となります。したがって,
8= |G|=|Cc1|・|C(c1)| = 4×2
なお,c2 の中心化群は c2 がすべての C4v の元と可換なので,Cc2={e,c1,c2,c3,σx,σy,σd,σd’}です。
a = e c2 c1,c3 σx,σy σd,σd’ 共役類 C(a)= {e} {c2} {c1,c3} {σx,σy} {σd,σd’} 中心化群 Ca= C4v C4v { e,c1,c2,c3 } {e,c2,σx,σy} {e,c2,σd,σd’}
中心化群の群表を書いておくと,
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 中心化群 { e,c1,c2,c3 } | 中心化群 {e,c2,σx,σy} | 中心化群 {e,c2,σd,σd’} |
これらが可逆な部分群であることは一目瞭然ですね。
[5] 中心化群の定義[#]において,a∈Gの固定部分群を考える代わりに,a → H (Gの部分集合) と置き換えて定義される群を正規化群といいます。
| 定義 部分集合 H (⊂G) と可換なG の元全体の集合, N (H) ={ g|gH=Hg ; ∃g∈G } または,{ g|gHg-1=H ; g∈G } を 「 H の正規化群」 という。 |
ここで,H はGの任意の部分集合でも構いませんが,重要なのは,H がGの部分群となっているときです。具体例 として,C4v でみておくと,
| 部分群 H= |
{e,σx },{e,σy } | {e,σd },{e,σd’} | {e,c1,c2,c3 },{e,c2,σx,σy}, {e,c2,σd,σd’},{e,c2 },{e} |
||
| 正規化群 N (H) = |
{e,c2,σx,σy} | {e,c2,σd,σd’} | C4v | ||
(1) 部分群 H={e,σx },および,{e,σy }の正規化群は,どちらもN (H) ={e,c2,σx,σy}である。
そして,HはN (H)の正規部分群[#]となっている。(N(H)より大きな群はHを正規部分群としない。)
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
| 正規化群 {e,c2,σx,σy} | ||||||||||||||||||||||||||||||||||||||||||||||||||||
(2) 部分群 H={e,σd },および,{e,σd’}の正規化群は,どちらもN (H) ={e,c2,σd,σd’}である。
そして,HはN (H)の正規部分群[#]となっている。
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
| 正規化群 {e,c2,σd,σd’} | ||||||||||||||||||||||||||||||||||||||||||||||||||||
(3) 部分群 H={e,c1,c2,c3 },{e,c2,σx,σy},および,{e,c2,σd,σd’}の正規化群は,どれもN (H) =C4v である。そして,HはN (H)の正規部分群[#]となっている。
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 正規化群 C4v H={e,c1,c2,c3 } |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 正規化群 C4v H={e,c2,σx,σy} |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 正規化群 C4v H={e,c2,σd,σd’} |
(4) 部分群 H={e,c2}の正規化群は,まず,N (H) =C4vである。
そして,HはC4vでの正規部分群となっています。
| X・Y | e | c2 | c1 | c3 | σx | σy | σd | σd’ |
| e | e | c2 | c1 | c3 | σx | σy | σd | σd’ |
| c2 | c2 | e | c3 | c1 | σy | σx | σd’ | σd |
| c1 | c1 | c3 | c2 | e | σd’ | σd | σx | σy |
| c3 | c3 | c1 | e | c2 | σd | σd’ | σy | σx |
| σx | σx | σy | σd | σd’ | e | c2 | c1 | c3 |
| σy | σy | σx | σd’ | σd | c2 | e | c3 | c1 |
| σd | σd | σd’ | σy | σx | c3 | c1 | e | c2 |
| σd’ | σd’ | σd | σx | σy | c1 | c3 | c2 | e |
ところが,この一部分を抜き出してもH={e,c2}を正規部分群とする部分群が以下のとおり存在します。
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| {e,c2,σx,σy} | {e,c1,c2,c3 } | {e,c2,σd,σd’} |
以上のまとめ
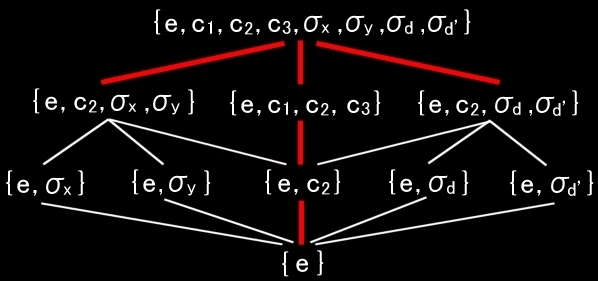 |
{e,c2 } =<c2> {e,c1,c2,c3 } =<c1> {e,c1,c2,c3,σx,σy,σd,σd’}=<c1,σx> |
| Hasse図 C4v (赤線: C4vの正規部分群) 白線は直上の群の正規部分群 |
|
| 生成元による表示 |
説明文はこちら, ⇒ Appendix 冪零群
命題1の証明
定理1の証明
C(a)からG/Caへ同型写像ψ(gag-1)=[g] が存在することを示せばよい。
gag-1∈C(a),[g],[h]∈G/Ca
関連項目:
| 定理 対称群Snの中心は,C(S2)=S2,および,C(Sn)={e} (n≧3) 交代群Anの中心は,C(A3)=A3,および,C(An)={e} (n≧4) |
点群で使われる記号 C4V
E={E}; C2={C42}; 2C4={C4、 C43}; 2σv={σx、σy}; 2σd={σd、σd’}
同じ類に属する既約表現のトレースは等しいという重要な性質があります。これを指標と呼びます。