ラグランジュの定理

| 7 固定部分群と ラグランジュの定理 |
 |
|
| f-denshi.com 最終更新日: 21/09/30 証明追加 | ||
| [目次へ] | ||
| サイト検索 | ||
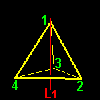
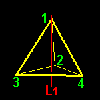
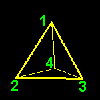
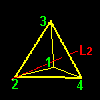
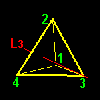
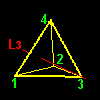
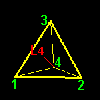
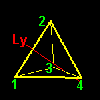
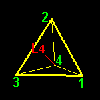
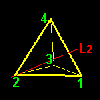
[1] もう一つ,前ページで求めた同値類の重要な特徴について述べましょう。G の元を視覚的に理解するために,G の元(=変換)が正四面体に作用した後の頂点の位置を同値類ごとに分類して,下図に示しました。
 |
 |
 |
 |
 |
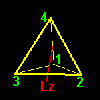 |
| G1=a1G1={a1,b1,e} | a2G1={a2,b3,hz} | ||||
 |
 |
 |
 |
 |
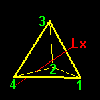 |
| a3G1={a3,b4,hy} | a4G1={a4,b2,hx} | ||||
この図で頂点1の位置に注目して下さい。同じ同値類に属する元は正四面体の頂点1を同じサイトに移す変換であることがわかりますね。これを写像を用いて書き表すならば,
頂点 1へ: a1(1)=1,b1(1)=1, e(1)=1
頂点4へ: a2(1)=4,b3(1)=4,hz(1)=4
頂点 2へ: a3(1)=2,b4(1)=2,hy(1)=2
頂点 3へ: a4(1)=3,b2(1)=3,hx(1)=3・・・・・・・・・・・・・・・・[**]
となっていることが理解できます。
前ページではS1という記号を用いましたが,ここでは,1∈Mを動かさない変換からなる固定部分群であることを意識して,G1という記号を使うこととしました。
この例では頂点1が特別な意味を持っていますが,これは上の剰余類別に用いた部分群G1に秘密が隠されているわけで,それはG1の元(変換)a1,b1,e がどれも頂点1を動かさない変換であることに理由があります。
[2] この結果は次の一般化された定理の具体例の一つとなっています。
| 定理1 群G が集合 M上に働いているとする。このとき,M の元:m0 のG軌道,G(m0) について, (1) G(m0) の元の個数は群 G の位数の約数である。 (2) G(m0)の元g(m0)と G の固定部分群 Gm0 による(左)剰余類gGm0とは 1対 1に対応する。 (14/10/17,具体的に書きなおしました。) (3) |G|=|Gm0|×|G(m0)| |
厳密な証明 ⇒ [#]
直感的に理解する方法↓
[3] 前ページで述べた軌道,固定部分群という用語を用いれば, m0=頂点1 の場合,
m0 のG軌道 ⇔ G(m0)= {頂点 1,2,3,4} (全部の正四面体サイトを動いてます)
固定部分群 ⇔ Gm0 = {a1,b1,e}, 頂点1を動かさない変換
|G|=12
という対応になっています。ここで定理の(1)と(3)は, |G(m0)|=4 ,|Gm0|=3 より OK
(2)は,[**]を参照すれば,
a1(1)=b1(1)= e(1)= 1 ⇔ a1G1=b1G1=eG1={a1,b1,e}
a2(1)=b3(1)=hz(1)=4 ⇔ a2G1=b3G1=hzG1={a2,b3,hz}
a3(1)=b4(1)=hy(1)=2 ⇔ a3G1=b4G1=hyG1={a3,b4,hy}
a4(1)=b2(1)=hx(1)=3 ⇔ a4G1=b2G1=hxG1={a4,b2,hx}
という 1対 1対応を考えることができます。
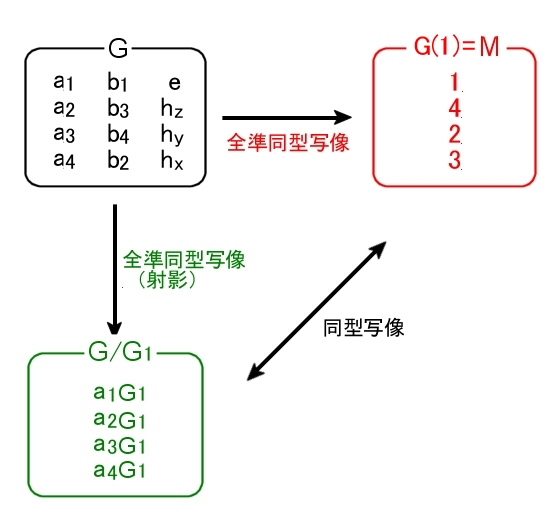
これを一般化,g∈G,1∈M として,
g(1) ⇔ gG1 ( ⇒ m0∈M とさらに一般化すると, g(m0) ⇔ gGm0 )
のような1対1写像を考えることができることが分かります。
[4]
| コーシーの定理 素数 p が|G|の約数であるならば,位数が p の元 g∈G が必ず存在する。 ⇒ gp=e |
正四面体群であれば,12=22・3 より素数 p は 2 と 3 である。実際,
(a1)3=(a2)3=(a3)3=(a4)3=e
(b1)3=(b2)3=(b3)3=(b4)3=e
(hx)2= (hy)2= (hz)2=e
と確かめられます。
[1] 次に S1 に替わって,Gの部分群 H={e,hx,hy,hz} を用いて G を類別してみましょう。
S1 の場合と同様に,正四面体の群表から同値関係 x・h,h∈H に基づいて一覧を作ります。
X・H e hx hy hz a1 a1 a2 a4 a3 a2 a2 a1 a3 a4 a3 a3 a4 a2 a1 a4 a4 a3 a1 a2 b1 b1 b4 b3 b2 b2 b2 b3 b4 b1 b3 b3 b2 b1 b4 b4 b4 b1 b2 b3 e e hx hy hz hx hx e hz hy hy hy hz e hx hz hz hy hx e
先ほどと同様に,
a1H=a2H=a3H=a4H ={a1,a2,a3,a4} = A
b1H=b2H=b3H=b4H ={b1,b2,b3,b4} = B
eH=hxH=hyH=hzH ={e, hx,hy,hz} = H
が確かめられます。すなわち,G は H によって3つの同値類 {a1,a2,a3,a4},{b1,b2,b3,b4},{e,hx,hy,hz}へ類別されてます。
[2] この H は固定部分群[#]ではないので,S1 に見出されるような頂点と剰余類(同値類)との関係はありません。
[3] 以上のように G を部分群 S1 および H を用いて類別しましたが,いずれの場合も同値類別に用いた部分群の位数と同値類の個数との積は群 G の位数に等しくなっています。すなわち,
12 = |G|=|S1|×|G:S1| = 3 × 4
12 = |G|=|H| ×|G:H| = 4 × 3
この関係は,すべての部分群について成り立つ関係で次のような定理として知られています。
| ラグランジュの定理 群 G の任意の部分群を H ,G における H の指数 [#] を|G:H|とすると, |G|=|H|×|G:H| |
変数はa,g,h∈G; m,n∈M とする。本文中のm0はここではmと書く。
まず,確認
G(m)={ g(m)|g∈G } [m軌道]
Gm={ g∈G|g(m)=m } [mの固定化部分群]
(2)の証明
a∈G,n=a(m) (n∈G(m)) であるとき,
{ g∈G|g(m)=n } は ⇔ 剰余類 aGm となっている。
ことを示したい。
← を示す。
gを剰余類 aGm の元とする,すなわち,h∈Gm ,g=ah とすると,
⇒ g(m)=(ah)(m)=a(h(m))=a(m)=n ⇔ gは{ }の元でもある。
→ を示す
g を{ }の元とすると,すなわち,g(m)=n とすると,
⇒ (a-1g)(m)=a-1(g(m))=a-1(n)=a-1(a(m))=m
⇔ (a-1g)∈Gm ⇔ gは剰余類 aGmの元でもある。
したがって, { g∈G|g(m)=n } ≡ Gm であり,
| G= | ∪ | { g∈G|g(m)=n } |
| n∈G(m) |
↓正四面体群の場合
G={ g∈G|g(m)=1 }∪{ g∈G|g(m)=2 }∪{ g∈G|g(m)=3 }∪{ g∈G|g(m)=4 }
↓特にm=1の場合
={a1,b1,e}∪{a2,b3,hz}∪{a3,b4,hy}∪{a4,b2,hx}