
| 13 同型定理 |  |
|
| f-denshi.com 最終更新日: 22/08/11 表の間違いを訂正しました | ||
| [目次へ] | ||
| サイト検索 | ||
[1] 群の同型の厳密な定義
|
定義 2つの群 G と G’が同型である必要十分条件は,φψ=ψφ=1 (恒等写像)となる準同形写像, φ: G ⇒ G’ が存在することである。 |
これはこれでいいでしょう。
[2]
|
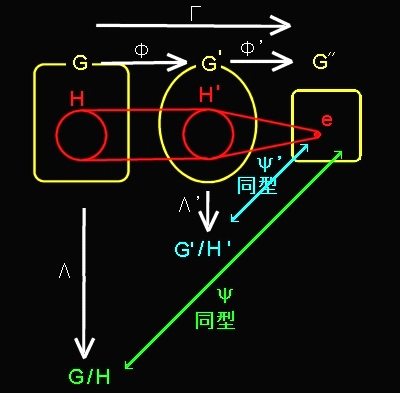
第1同型定理 群 G から群 G’への上への準同型写像を Φとする。H’を G’の正規部分群,また,Φ-1(H’)=H とすると, G/H と G’/H’ とは同型である。 |
[3]
証明
上図を参考にしてください。
(1) H’が G’の正規部分群なので,
(A) G’/ H’ に同型な群 G”
への上への同型写像Ψ’が存在する。
(2) 次に合成写像,Γ=Φ’・Φ を考えると,
これは G から G”への上への準同型写像で,H∈G は KerΓなので,準同型定理より,
(B) G/H と G”との間には同型写像Ψが存在する。
⇒(A),(B)より G/H と G’/H’は同型。(もちろん,これらは G”とも同型。)
[4]
例 次の加群(可換群)を考えよ。
↑ 百聞は一見に如かず!
[5]
|
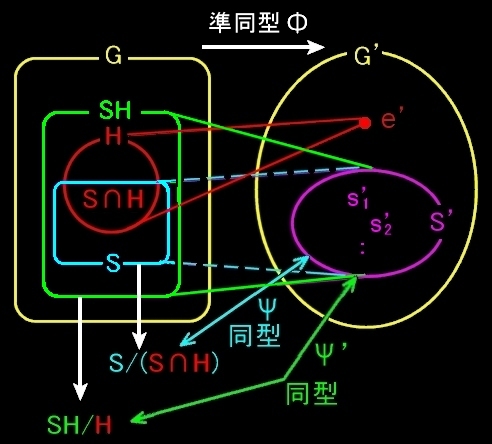
第2同型定理 群 G の正規部分群を H,また,G の任意の部分群を S とする。このとき, S∩H は S の正規部分群 であって, SH/H と S/(H∩S) とは同型である。 ( 加群の記号では,SH ⇔ S+H ) |
[6]
証明
上図が理解できれば,自明な定理です。
(1) Gの正規部分群が H ならば,準同型定理から G/H に同型な群 G’への準同型写像Φが存在して,
Φ(H)=e’ (=G’の単位元,H=KerΦ)
となっている。
準同型写像 Φ(SH)=S’を考えよう。
(2) G の部分群 S の元全体がΦによって写る像をΦ(S)=S’とする。
逆に準同型写像Φによって S’に写ってくる G の元全体Φ-1(S’) は S だけではなく,
SH={ sh|s∈S,h∈H } ←同値類 sH,∀s∈S を構成するGの元全体
である。
(3) H は SH の正規部分群でもある。( H ⊂ SH ⊂ G から自明。)
したがって,準同型定理より,
(A) SH/H=S’
が成り立っている。
準同型写像 Φ(S)=S’を考えよう。
(4) 一方,Sの元の中でS∩Hに属する元はΦによってe’ に写るので,Sの核はS∩Hであることが分かる。
( S∩H は S の正規部分群 )
したがって,Sに制限した準同型写像に準同型定理を用いれば,
(B) S/(S∩H)=S’
が成り立つ。
(5) (A) と (B) とを合わせて考えれば, (S’を介して)
SH/H = S/(H∩S) [同型]
であることがわかる。 証明終
[7]
具体例 下をみよ。・・・・・右を見よ。 一番下の囲みを見よ
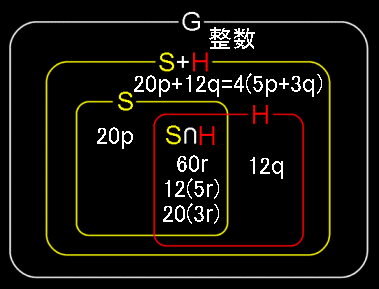
加群 {元} G Z z S 20Z 20p H 12Z 12q H∩S 60Z 60r H+S 4Z 4z
z,p,q,r ∈ 整数
4Z/12Z = 20Z/60Z
[8]
|
第3同型定理 群 G の正規部分群を N,H,ただし,N ⊂ H とする。このとき, G/H と (G/N)/(H/N) とは同型である。 |
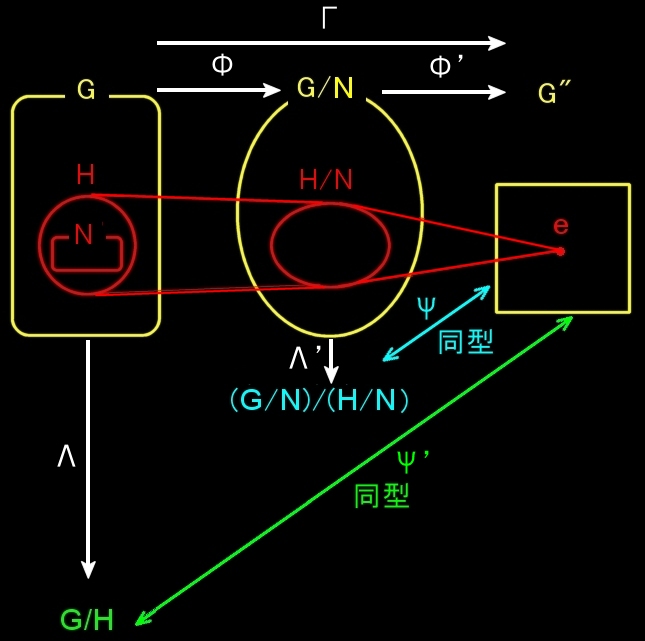
証明
(1) この定理は第1同型定理において,G’→G/N と置き換えただけです。
(2) そのとき,第1同型定理の H’は,H/N に置き換える必要があります。なぜならば,準同型写像Φによって,hKerΦ,h∈H に含まれるGの点はすべて同値類 hN∈G/N へまとまって写されるからです[#] 。
(3) 上の図を参照すると,第1同型定理とまったく同様に G”を介して,G/H と (G/N)/(H/N) とが同型であることを示すことができます。
証明終
例 下をみよ。・・・・・さら下を見よ。 それを一番下の囲みと比較せよ。
加群 {元} G Z ・・・,-3,-2,-1,0,1,2,3,・・・ H 3Z ・・・,-12,-9,-6,-3,0,3,6,9,12,・・・ N 12Z ・・・,-24,-12,0,12,24,・・・ G/H Z/3Z [0]3,[1]3,[2]3 G/N Z/12Z [0]12,[1]12,[2]12,[3]12,[4]12,[5]12,[6]12,[7]12,[8]12,[9]12,[10]12,[11]12 H/N 3Z/12Z [0]12,[3]12,[6]12,[9]12
↑ 以前,H と N が逆になっており,訂正しました。ご指摘ありがとうございました。 (22/08/11)
以上の記号の下で,
[0]3,[1]3,[2]3 〜 [0]12,[1]12,[2]12,[3]12,[4]12,[5]12,[6]12,[7]12,[8]12,[9]12,[10]12,[11]12 [0]12,[3]12,[6]12,[9]12
↓↑
Z/3Z = [Z/12Z]/[3Z/12Z]
要するに同じ (ここでは12を) 法とする剰余類どうしからさらに剰余類をつくることができるための条件について,第3同型定理は述べていると考えるとわかりやすい。それは可換群であること,大きい剰余類の個数を小さい剰余類の個数で割り切れることで,正規部分群,剰余群の用語を使って正確に述べれば定理のとおりとなります。