
| 12 準同型定理 |  |
|
| f-denshi.com 最終更新日: 23/04/11 | ||
| [目次へ] | ||
| サイト検索 | ||
[1] 整数 Z から剰余群 Znへの写像 Φ:a → [a]n (=Φ(a))を考えます。このとき,すべての a,b∈Z について,
Φ(a+b)=Φ(a)+Φ(b) ← [a+b]n=[a]n+[b]n
が成り立っていました。このとき,
a + b = c :整数の加法
↓ ↓ ↓Φ
Φ(a) + Φ(b) = Φ(c) :剰余群の加法
( [a]n + [b]n = [a+b]n =[c]n )
の対応が成立しますが,このような写像 Φ は準同型写像と呼ばれます。
[2] 準同型写像の一般的な(厳密な)定義は以下のとおりです。
| 定義 群(G,* )から,群(G’,* )の中への写像 Φ : g → Φ(g), ( g∈G, Φ(g)∈G’ ) が任意の a,b∈G に対して, Φ(a*b)=Φ(a)*Φ(b) をみたすとき,Φ を G から G’への準同型写像という。 ( もちろん,演算として+,+ を用いても同じです。) (φは必ずしも全射である必要はない。) |
このとき,最も基本的は関係として,
| 命題 Φが準同型写像であれば, (1) Φ(e)=e’ が成り立つ。 |
ここで,Φ(g)-1∈G’は,Φ(g)の逆元です。 なお,Φ-1(g’)∈G におけるΦ-1はΦの逆写像という意味なので混同しないように。
証明
(1) 準同型写像の定義より,
Φ(e)=Φ(e*e)=Φ(e)*Φ(e)
Φ-1(e)を両辺に掛けて。
(e’=) Φ-1(e)*Φ(e)=Φ-1(e)*Φ(e)*Φ(e)=e’*Φ(e)=Φ(e)
(2) 準同型写像の定義より,
e’=Φ(g*g-1)=Φ(g)*Φ(g-1)
両端を着目すると,Φ(g-1)はΦ(g)の逆元Φ(g)-1に等しいことが分かる。 (終)
例
正四面体群 G={ e,hx,hy,hz,a1,a2,a3,a4,b1,b2,b3,b4 }[#] から3文字の巡回群 Z3= { e’,t1,t2 } [#] への写像を以下の通り定めると,
Φ(e)=Φ(hx)=Φ(hy)=Φ(hz)=e’
Φ(a1)=Φ(a2)=Φ(a3)=Φ(a4)=t1
Φ(b1)=Φ(b2)=Φ(b3)=Φ(b4)=t2
Φ: G→Z3 は準同型写像となります。実際,
Φ(ak*ak)=Φ(bk)=t2=t1*t1=Φ(ak)*Φ(ak)
Φ(ak*bk)=Φ(e)=e’=t1*t2=Φ(ak)*Φ(bk)
・・・・・・・・・・
Φ(hx*hy)=Φ(hz)=e’=e’*e’=Φ(hx)*Φ(hy)
・・・・・・・・・・
などと準同型定理の定義を満足していることをすべて確かめることができます。
あるいは,
Φ(ak-1)=Φ(bk)=t2=t1-1=Φ(ak)-1
Φ(hk-1)=Φ(hk)=e’=e’-1=Φ(hk)-1
などを確認してもよいでしょう。
ついでに述べておくと,このような Φ が,さらに群 G から群 G’への
(1)1対1写像(単射),
(2)上への写像(全射)
という両条件をみたすときは同型写像と呼ばれます。その場合,G と G’は群として全く同じ構造をもっているといえます。
写像,Φ:Z → Zn の場合は,1対1写像ではありませんが,Zn の上への写像(全射)となっています。この場合,上への準同型写像(または,全準同型写像)と呼ばれます。
[3] ここで,準同型写像において重要な用語を一つ定義しておきましょう。
核の定義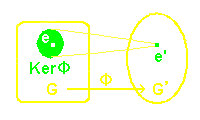 群G(単位元: e )から群G’(単位元: e’)への準同型写像を Φとする。このとき,Φ によって群 G’の単位元 e’に移される G の元すべてからなる G の部分集合,すなわち, Ker Φ={g|Φ(g)=e’,g∈G }を Φの核といい,Ker Φと書く。 |
整数の集合,Z から剰余類群,Znへの準同型写像 Φ の核は: Ker Φ=nZ です。つまり,n の倍数はΦによって,すべて Zn の単位元 [0]n へ写されています。
[4] この用語を用いて,これまでみてきたことを一般化すると,
| 定理1 群 G から群 G’への任意の準同型写像Φについて, (1) Φの核 Ker Φ は G の正規部分群である。 (2) 群 G’の正規部分群 H’に対して,Φ-1(H’)={h|Φ(h)∈H’,h∈G }は G の正規部分群である。 (3) また,g’∈G’; Φ(g)=g’のとき,この逆像: Φ-1(g’)={x|Φ(x)=g’,x∈G } を考えるとこれは Ker Φによるの剰余類の一つ,”g KerΦ” に等しい。 (←左・右剰余類は等しい) |
と言うことができます。
[5]
[略証]
(1) Ker Φ が正規部分群であることは,すべての g に対して,g-1Hg ⊂ H=KerΦ を示せばよい。[#]
任意の h ∈ KerΦ をとると,どんな g ∈ G に対しても,
Φ(g*h*g-1)=Φ(g)*Φ(h)*Φ(g-1)
= Φ(g)*e’*Φ(g)-1=Φ(g)*Φ(g)-1
=e’
したがって,g*h*g-1 ∈KerΦ,ここで,h は核の任意の元なので,g-1Hg ⊂ KerΦ。
(2) H =Φ-1(H’)とおくと,任意の h ∈ H について Φ(h)∈H’であり,任意の g∈G に対して,
Φ(g*h*g-1)=Φ(g)*Φ(h)*Φ(g-1)∈H’ ∵ H’は正規部分群なので最後の∈がいえる。
すなわち,任意の h∈H について,g*h*g-1 ∈ H ⇒ g*H*g-1 ⊂ H 。 よって,H は G の正規部分群。
(3) 証明の前にこの定理のかみ砕いた言い方をしておくと,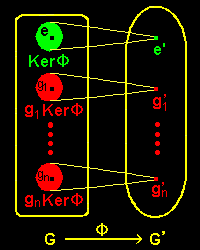
G (Z)の部分集合,Ker Φ (nZ) の元が Φによって ”すべて”,G’のひとつの点 e’([0]n)に移されるように,G の部分集合 g1Ker Φ(g1+nZ )はそっくりすべて,G’のひとつの点 g1’点 ([g1]n )に移される。(右図)
ことを述べています。
証明は,x∈Φ-1(g’),Φ(g)=g’ ならば,
Φ(x)=g’ ⇒ Φ(x)=Φ(g)=g’
また,Φ(g)-1=Φ(g-1) なので,
e’=Φ(g)-1*Φ(g)=Φ(g-1)*Φ(x)
=Φ(g-1x)
すなわち,
g-1x ∈ Ker Φ ⇔ x∈ g KerΦ
逆に,x=gKerΦ ならば,
Φ(x)=Φ(g)Φ(kerΦ)=Φ(g)e’=g’
よって,gKerΦとg’が1対1に対応している。
これは,g=gk (k=1,2,…,n)について成り立つ。
| 定理2 準同型定理 群G から群 G’への上への準同型写像をΦとするとき( ImΦ=G’),G/KerΦ と G’は同型である。 具体的には,G/KerΦの元を剰余類の記号を用いて,gj KerΦと書くとき, Ψ(gj KerΦ)=g'j ;ただし,Φ(gj)=g'j ∈G’ と定めればよい。 |
上へのという条件がないときでも,G/KerΦ と Im Φ⊂ G’は同型である,と述べることはできる。
[1]
例の解説はクドイので削除しました。
[2] この準同型定理の一般的な証明を書いておきましょう。
準同型定理
(1) 群Gの正規部分群をH,その剰余群をG/Hとする。このとき,
Λ: G → G/H [ 射影 :標準的全準同型写像]
すなわち,
Λ(g)=gH : g∈G,gH∈G/H
とするとき,剰余類の積はΛを用いれば,
(gjH)(gkH)=gjgkH ⇔ Λ(gj)Λ(gk)=Λ(gjgk)
と表されるので,Λは(標準的)全準同型写像である。
(2) 定理1より,GからG’への準同型写像Φの核 KerΦは,Gの正規部分群であるからこれを同じHで表すこととする。
G のH による剰余群 (等質集合) G/H= {g0H=H,g1H,・・・}から G’への1対1写像を,
Ψ: G/H → G’
ただし,
Ψ(g0H)=Φ(g0), Ψ(g1H)=Φ(g2),・・・
と定義する。
ここで,仮定よりΦが全射なので,任意のg’∈G’に対して,Φ(g)=g’ となる g が存在する。
また,Λも全射であるから Ψ(Λ(g))=Φ(g)=g’ を考えるとΨは全射である。
(3) gj とgk が同じ同値類に属することは,定理1-(3) より,Φ(gj)=Φ(gk) と同じことである。すると,
Ψ(gjH)=Ψ(gkH) ⇔ Φ(gj)=Φ(gk) ならば,gjH=gkH
であるから,Ψは単射であり,(2)の結論と合わせて,Ψは全単射である。
(5) さらに,Φが準同型写像であることを利用して,
Ψ(gjH*gkH)=Ψ(gjgkH)=Φ(gj*gk)=Φ(gj)*Φ(gk)=Ψ(gjH)*Ψ(gkH)
よって,Ψは準同型写像である。以上より,Ψは同型写像である。
この定理を成り立たせているポイントは,「KerΦがGの正規部分群である」というところです。
[3] 連続濃度の元を持つ群に対する例を一つ挙げておきます。
群の元が離散的でない乗法群 C* から R+への準同型写像
Φ(c)=|c|
を考えます。この写像が準同型であることは容易に確かめられます。
この写像によって複素平面単位円上の点はすべて,乗法群 R* の単位元 1 に写されますから,
KerΦ=exp (iθ),0≦θ<2π (半径1の円で S1 と書く)
が核 [#] であることが分かります。
すると,準同型定理によって,剰余群
C*/S1={r|reiθ/eiθ,r>0,0≦θ<2π}
は,
ImΦ=R*
と同型であることが分かります。
これを図で示すと下のように表すことができます。
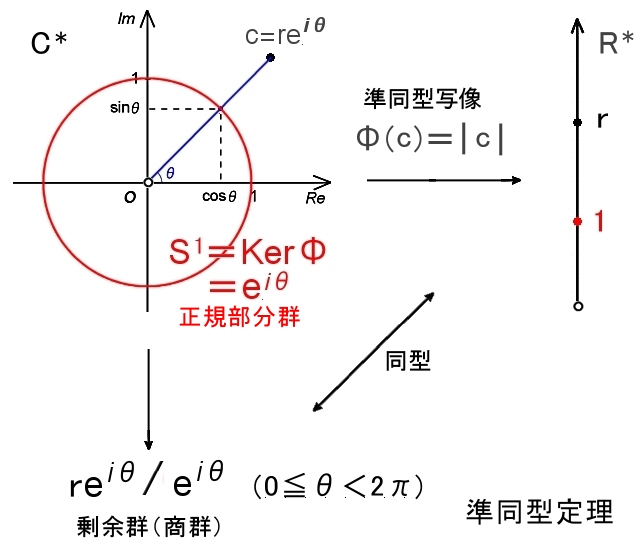
R+={x∈R|x>0}
C*=C−{0}
集合の元の間に演算が与えられてなくても準同型定理と同様な定理が成り立ちます。
集合G の元 g に同値関係 〜 が与えられていて,その同値類 [g] の全体集合を
G/〜 とします。
このとき,G から G/〜 の全射を考えることができるが,これを自然な射影と呼びます。
ここで,集合G から集合G’への写像Φとして,
g〜g' ⇒ Φ(g)=Φ(g')
を満たすものを考えると,集合 G/〜 から G’への写像Ψ が誘導され,
Φ=ΨΛ : Φ(g)=Ψ([g])=Ψ(Λ(g))=ΨΛ(g)
という関係があります。このとき,
| 定理 (準同型定理の系) 次の2つが成り立つ。 (1) 集合G から集合G’への写像Φが全射ならば,Ψ: (G/〜) → G’ は全射である。 (2) g1,g2∈G が,「 g1〜g2 ⇔ Φ(g1)=Φ(g2) 」 ならば,Ψ: (G/〜) → G’ は単射である。 特に (1),(2)が同時に成り立てば,Ψは同形写像となる。 |
定理2の系 (集合の演算を考えない場合よりこちらの方が条件はゆるい) です。
証明
(1)
Φ=ΨΛ (Λは全射) であるから,Φが全射であれば,Ψも全射である。
(2)
Ψ([g1])=Ψ([g2]) であれば,Φ(g1)=Φ(g2) であるが,「 Φ(g1)=Φ(g2) ⇒ g1〜g2 」 も成り立つならば,
Ψ([g1])=Ψ([g2]) ⇒ g1〜g2 ⇔ [g1]=[g2]
よって,Ψは単射である。
具体例を挙げておきます。
例
実数の全体集合Rに同値関係〜として,
「 r,r'∈Rに対して,rーr' ∈ 整数の全体集合Z 」
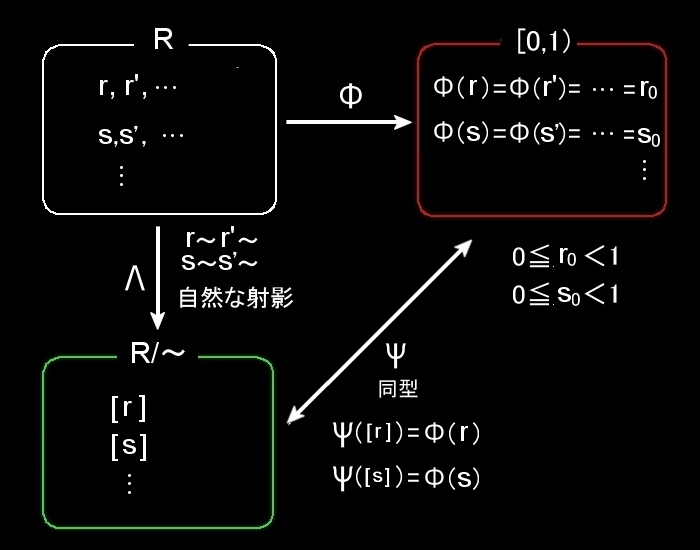
を定めると,RからR/〜の自然な射影Λが定まる。ここで,
Λ(r)=[r]={ x|x-r ∈ Z }
また,Rから実数の半開区間 [0,1) への全射Φとして,
rーr' ∈ Z ⇔ Φ(r)=Φ(r')=r0, 0≦r0<1
( r=r0+m,r'=r0+m’; m,m’∈Z ,0≦r0<1)
を定めると同型写像,
Ψ: R/〜 ⇒ [0,1)
が誘導され,
Φ(r)=Ψ([r])=Ψ(Λ(r)) ⇔ Φ=ΨΛ
が成立している。つまり,集合として,R/〜 ≡ [01) である。
|
定理: (1)巡回群 Zn から Zm への準同型写像の個数は m と n の最大公約数に等しい。 (2)特にmとnが素のときは,準同型写像Φは, |
加群では,e → 0 , 零写像 Φ(z)=0 ∈Zm とみなす。
例 Φ:Z6→Z3とZ3 →Z6 において最大公約数は3なので,それぞれ,以下のような3つの準同型写像が存在する。
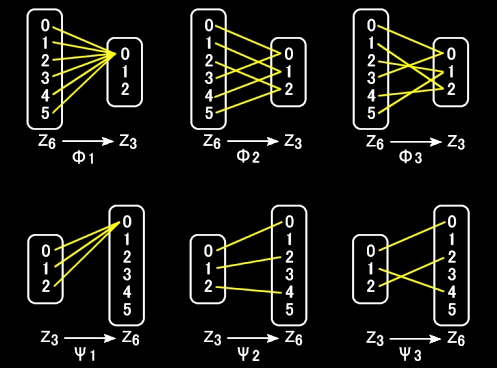
ここで,Φ2,および,Φ3は全射であり,ともに,核:KerΦ={[0]6,[3]6}であるが,
剰余群 Z6/{[0]6,[3]6}
を考えることが可能で,これはZ3:{[0]3,[1]3,[2]3}と同型である。
古典群
準同形写像の例
| 準同型写像 | 核 | 準同形定理 | 半直積 | |
| 乗法群 R* ⇒ R+ | f(x)=|x| | S0 | R*/ S0= R+ | R*=S0 R+ |
| 乗法群 C* ⇒ R+ | f(c)=|c| | S1 | C*/ S1= R+ | C*=S1R+ |
| 加群 R ⇒群 S1 | f(x)=e2πi x | Z | R/Z=S1 | R=ZS1 |
| GL(n,K)⇒K* | f(A)=detA | SL(n,K) | GL(n,K)/SL(n,K)=K* | GL(n,K)=SL(n,K)K* |
| O(n)⇒S0 | f(A)=detA | SO(n) | O(n)/SO(n)=S0 | O(n)=SO(n)S0 |
| U(n)⇒S1 | f(A)=detA | SU(n) | U(n)/SU(n)=S1 |
U(n)=SU(n)S1 |
| A(Rn)⇒GL(n,R) | f(Ax+σ)=A | D(Rn) | A(Rn)/D(Rn)=GL(n,R) | A(Rn)=D(Rn)GL(n,R) |
| E(Rn)⇒O(n,R) | f(Ax+σ)=A | D(Rn) |
E(Rn)/D(Rn)=O(n,R) |
E(Rn)=D(Rn)O(n,R) |
| SO(n+1) ⇒ Sn SO(3) ⇒ S2 |
SO(n) SO(2) |
SO(n+1)/SO(n)=Sn SO(3)/SO(2)=S2 |
SO(n+1)=SO(n)Sn SO(3)=SO(2)S2 |
|
| O(n+1) ⇒ Sn O(3) ⇒ S2 |
O(n) O(2) |
O(n+1)/O(n)=Sn O(3)/O(2)=S2 |
||
| Sn⇒Z2 | f(σ)=sgnσ | An | Sn/An=Z2 | Sn=AnZ2 |
| Dn ⇒Z2 | f(ci)=1 f(ciσ)=-1 |
Zn={ci} | Dn/Zn=Z2 | Dn/Zn=Z2 |
| 4元数群 Q⇒Z2 |
f(±1,±i)=1 f(±j,±k)=-1 |
Z4 | Q/Z4=Z2 | |
A∈ Mn 実n次正方行列,
K*=K−{0}
R*=R−{0}
R+={x∈R|x>0}
C*=C−{0}
S0={x∈R | |x|=1}={1,-1}
S1={c∈C | |c|=1}={eiθ}
行列,
| S0= | 1 | 0 | ・・ | 0 | , | -1 | 0 | ・・ | 0 | ||||||
| 0 | 1 | ・・ | ・・ | 0 | 1 | ・・ | ・・ | ||||||||
| ・・ | ・・ | 1 | 0 | ・・ | ・・ | 1 | 0 | ||||||||
| 0 | ・・ | 0 | 1 | 0 | ・・ | 0 | 1 |
| S1= | , | a | 0 | ・・ | 0 | |||
| 0 | 1 | ・・ | ・・ | |||||
| ・・ | ・・ | 1 | 0 | |||||
| 0 | ・・ | 0 | 1 |