
| 10 5次方程式 |  |
|
| f-denshi.com 最終更新日: | ||
| [目次へ] | ||
| サイト検索 | ||
Zn*=(Z/nZ)*
| 命題 剰余群の直積分解 正整数 n が n=psqtru と素因数分解できるとき, (Z/(psqtru)Z)*=(Z/psZ)*×(Z/qtZ)*×(Z/ruZ)*とのように直積分解でき,(Z/psZ)* ,(Z/qtZ)*,(Z/ruZ)* は巡回群である。 n=2s のとき, (Z/2sZ)*=(Z/2s-2Z)×(Z/2Z) [巡回群×巡回群]p=奇素数 (Z/psZ)*=(Z/ps-1Z)×(Z/(p−1)Z) [巡回群×巡回群]もっとも簡単な場合では (Z/pZ)* ≡ Z/(p−1)Z [巡回群] |
簡単なので証明はパス。
[1]
最も簡単な n次代数方程式 xn−1=0 は円分方程式と呼ばれます。また,多項式 xn−1の分解体を円分体といいます。ガウス平面を利用すれば,その根は,半径1の円周上にあり,点 (1,0) を含み,円を n 等分する点の集合となっています。
| 円分多項式 Φn(x) とは,1の原始 n 乗根 [#] を過不足なくもつ多項式のことである。 |
例を n=10 まで挙げると,
Φ1(x)=x−1
| Φ2(x)=x−(-1)= |
|
|
| = |
|
=x+1 |
| Φ3(x)=(x−ω)(x−ω2)= |
|
= |
|
| = |
|
=x2+x+1 |
| Φ4(x)=(x−i )(x−i 3)= |
|
= |
|
| = |
|
=x2+1 |
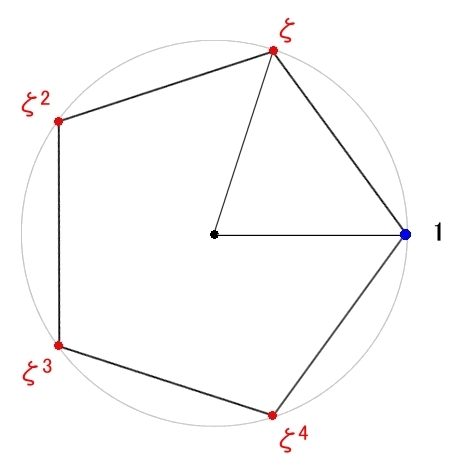
| Φ5(x)=(x−ζ)(x−ζ2)(x−ζ3)(x−ζ4)= |
|
= |
|
| = |
|
=x4+x3+x2+x+1 |
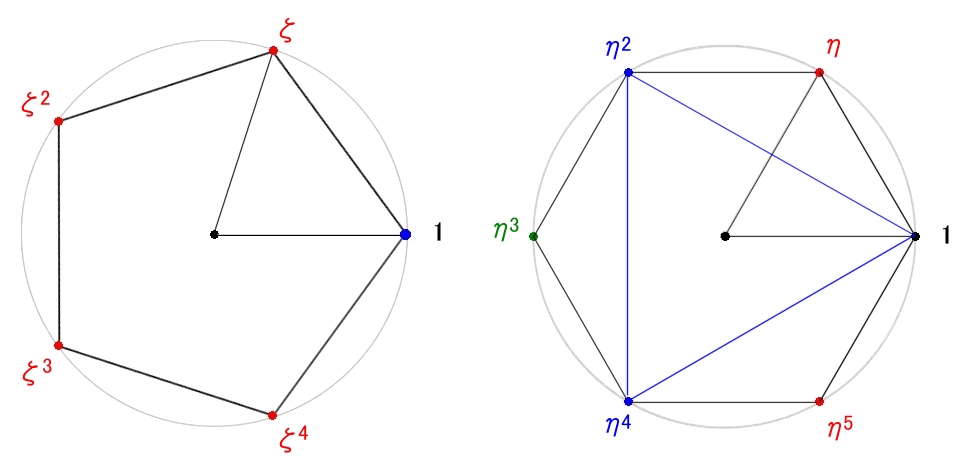
| Φ6(x)=(x−η)(x−η5)= |
|
= |
|
| = |
|
=x2−x+1 |
Φ7(x) =x6+x5+x4+x3+x2+x+1
Φ8(x) =x4+1
Φ9(x) =x6+x3+1
Φ10(x) =x4−x3+x2−x+1
Φ11(x) =x10+x9+x8+x7+x6+x5+x4+x3+x2+x+1
Φ12(x) =x4−x2+1
公式
|
などです。
[2]
| 命題 (1) 円分多項式 Φn(x) の次数はオイラーのPhi関数φ(n) [#] で与えられる。 (2) 円分多項式 Φn(x) は既約である。 |
証明
(1) 円分多項式の1次の因数 (xーζk) は nと素なkだけを拾い出しているので明らか。
n=10まで書いておくと,
| n= | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| φ(n)= | 1 | 1 | 2 | 2 | 4 | 2 | 6 | 4 | 6 | 4 |
| nと素なk= | 1 | 1 | 1,2 | 1,3 | 1,2,3,4 | 1,5 | 1,2,3,4,5,6 | 1,3,5,7 | 1,2,4,5,7,8 | 1,3,7,9 |
(n=1 については k=1 と定める。)
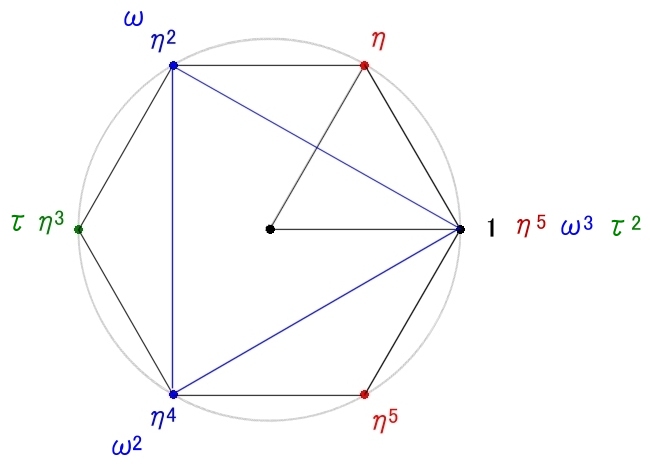
(2)の方は,具体例 n=6 の場合を一つ見てから証明に進みましょう。
x6−1は Q上既約でなく,次のように4つ因数の積に因数分解されます [#]。
x6−1=Φ6(x)Φ3(x)Φ2(x)Φ1(x)
= (x2−x+1) ・ (x2+x+1) ・ (x+1) ・ (x−1) ηの最小多項式 ωの最小多項式 τの最小多項式 1の最小多項式 原始根→ η ω (=η2) τ(=η3) η6=ω3=τ2=1
したがって,一つの最小多項式の共役根が,x6−1のすべての根を網羅することにはなりません。特徴を列挙すると,
(a) 4つのいずれもが既約多項式であり,互いに素であることは簡単に確かめられる。
(b) 4つの既約多項式は共通根はもたない。
(c) η,ω,τ,いずれも巡回群 (Z6の部分群) の原始根で,群の位数はいずれも n=6 の約数となっています。
[3] 以上を念頭におき,・・・
(1) 円分多項式Φn(x) の定義は,1の原始 n 乗根を一つずつすべて根にもち,
Φn(x) = Π(x-ζ) ←Πは,ζは1の原始 n 乗根全体にわたる。
とかける。
また,1の原始 n 乗根を1つζを選び出して,ζのQ上の最小多項式を φ(x) とする。
このとき、φ(x)=Φn(x) であることを背理法で示したい。
(2) 最小多項式の定義により、
φ(x) はΦn(x) を割り切る。
かつ,「φ(x) は,ある 1の原始 n 乗根を根に持たない」と仮定する。
すなわち,ある自然数 k があって、
φ(ζk) ≠0 ←この仮定から矛盾を導く
と仮定する。このような k が複数あれば,最小な k を選んでおく。
(3) 次に,ζk の Q 上の最小多項式を g(x) とすると,g(ζk)=0 であり,φ(x) と g(x) は互いに素で,
g(x) はΦn(x)を割り切る。
⇒ φ(x)g(x) はΦn(x)を割り切る。
(4) さらに,次の公式
xn-1 = Π Φd(x) ← x5−1=Φ6(x)Φ3(x)Φ2(x)Φ1(x) の一般化 d|n
を考えれば,
φ(x)g(x) は xn-1 を割り切る。 ・・・ [*]
ことが分かる。
(5) ここで, k を 割り切る素数 p を選ぶと,(p=1,k しか選べないときは定理は成り立つので,p≠1,k として話を進める)
η = ζ(k/p)
が存在して,k は φ(x) の根でないζk の最小の指数であるから、
η(<k) はφ(x)の根で,φ(η)=0
となる。
(6) 一方,xn-1 は Fp[x] の多項式としてみなしたときも重根を持たない。
(↑ xn-1 の微分 nxn-1 とは共通解もたない。)
ここで,
h(x)=g(xp)
を考えると,
h(η)=g(ηp)=g(ζk)=0 ← (3)より
h(x) はηを根にもつので、h(x)=φ(x)d(x) を満たす多項式 d(x) が存在する。 ←φ(η)=0 より
(7) さらに,Fp[x] の多項式としてみたときでも、[h(x)]=[φ(x)][d(x)] であるが、Fp[x]上では,h(x)=g(xp)=g(x)p であるから[#],
[g(x)]p=[φ(x)] [d(x)] [g(η)]p=[φ(η)] [d(η)]=0
である。つまり,それらを Fp[x] の多項式としてみたとき,
φ(x) と g(x) は共通根ηを持っている。
すると、φ(x)g(x) | xn-1 [*] 式を Fp[x] で考えた場合に、xn-1 は重根ηをもっていることになる。
これは円分多項式の定義 (公式) と矛盾する。
(8) よって,仮定:「あるkが存在して,φ(ζk) ≠0 ]は誤り。⇔ 「φ(x) は全ての1の原始 n 乗根を根にもつ。」 ⇒ φ(x)=Φn(x) でなければならない。(終)
[4]
| 定理 1の n 乗根はべき根で表すことができる。 |
証明は数学的帰納法による
(1) .n=1,2,3,4 の場合はすでにベキ根が求められている。
(2) nのとき成り立つならば,n+1のときも成り立つことを示せばよい。
(3) nが合成数ならばnより小さい場合に次のように帰着される。
n=pq
1のベキ根で表したp乗根をζ
1のベキ根で表したq乗根をη
とするとき,
xpq−1=(xq)p−1=Π0≦k≦p-1 (xq−ζk)
よって,
x=(ηm) ・ q ζk
( 0≦k≦p-1, 0≦m≦q-1 )
(4) nが素数pの場合だけ示せばよい。
ガウスの方法?: n=p(素数)の場合の根をn=p−1の場合の根のべき根を用いて表せることを示せばよい。
[5]
例
f(x)=x5−1 の根ηをx4ー1の根τのべき根で表す。
η5=τ4=1を繰り返し用いて,
f(η,τ)=η3+η3・3τ+η3.・3・.3τ2+η3.・3・3.・3τ3
=η3+η4τ+η2τ2+ητ3
f(η2,τ)4=(η+η3τ+η4τ2+η2τ3)4={τ(ητ3+η3+η4τ+η2τ2)4
=(η3+η4τ+η2τ2+ητ3)4
=f(η,τ)4
f(η3,τ)4=(η4+η2τ+ητ2+η3τ3)4={τ3(η4τ+η2τ2+ητ3+η3)4
=f(η,τ)4
f(η4,τ)4=f(η,τ)4
同様な計算をτ→τk に対して行うことができて, (τk)4=なので
f(η,τk)4=f(η2,τk)4=f(η3,τk)4=f(η4,τk)4 ・・・・ (1)
となる。
一方,η5=1 に注意して,
f(η,τ)4=(η3+η4x+η2x2+ηx3)4=a0(x)η3+a1(x)η4+a2(x)η2+a3(x)η
とηの展開係数をおくと,
f(η2,τ)4=a0(x)η2・3+a1(x)η2・4+a2(x)η2・2+a3(x)η2=a0(x)η+a1(x)η3+a2(x)η4+a3(x)η2
f(η3,τ)4=a0(x)η3・3+a1(x)η3・4+a2(x)η3・2+a3(x)η3=a0(x)η4+a1(x)η2+a2(x)η+a3(x)η3
f(η4,τ)4=a0(x)η4・3+a1(x)η4・4+a2(x)η4・2+a3(x)η4=a0(x)η2+a1(x)η+a2(x)η3+a3(x)η4
以上の4式を足し合わせると,
| f(ηm,τ)4=(a0(x)+a1(x)+a2(x)+a3(x))(η+η2+η3+η4) | |||
=−(a0(x)+a1(x)+a2(x)+a3(x))
=4a(x)
ここで,x→τk とおくと,
f(ηm,τk)4=4a(τk) k=0,1,2,3 ・・・・ (2)
(1),(2) より
f(η,τk)4=a(τk) ⇔ f(η,τk) =
a(τk)
⇔
η3+η4τk+η2τ2k+ητ3k=
a(τk) k=0,1,2,3
この4式 (k=0,1,2,3) を,η,η2,η3,η4の4つを未知数とする4元連立1次方程式と考えて,解くと,
η=
1 4 τk ・
a(τk)
これは,1の5乗根をηを次数の低い1の4乗根τのべき根で表している。
任意の素数 p に対しては,
ζ=
1 p-1
p-1 Σ k=1 ξk ・
p-1 a(ξk)
ζp=ξp-1=1 の原始根
となるはず。
[6] 関連した命題
| 命題 1の原始 n 乗根をζとするとき, [ Q(ζ):Q ]=φ(n) |
証明 二項拡大のところを見てください。
[1] F上の既約二項式 xn−a=0 の分解体 K を二項拡大体といいます。
| 定理 体 Q に1の原始 n 乗根の一つζを添加した (中間) 体を F=Q(ζ) とするとき,
に対応するガロア群, は巡回群となる。このベキ根拡大をクンマー拡大という。 |
ガロア拡大 K/Q に対応するガロア群 G(K/Q) が巡回群であるとき,K/Qを巡回拡大といいますが,特に,ガロア拡大がべき根拡大である場合にクンマー拡大といいます。
また,K/F に中間体の列が存在して,
F=M0 ⊂ M1 ⊂ M2 ⊂ ・・・ ⊂ Mm-1⊂ Mm = K
Mi/Mi-1 は二項拡大 ( i = 1, 2, ・ ・ ・ , m )
となっているとき,K/F を 累ベキ根拡大といいます。
[2]
証明
例を見た方が分かりやすい(自明)でしょう。
例1 n=5 素数の場合 x5ーa=0
x5ーa=(x−α)(x−αζ)(x−αζ2)(x−αζ3)(x−αζ4)
ここで,5√a=α,ζは1の5乗根の一つです。
Q上の自己同型写像σab を次のように定義することができます。
σab(q)=q (q∈Q)
σab(ζ)=ζa (a=1,2,3,4 )
σab(α)=αζb (b=0,1,2,3,4 )
σab(αζ)=αζa+b (mod 5)
これらは写像の合成を算法として群をなすことは容易に確かめられます。例えば,
σcdσab(αζ)=σcd(αζa+b)=αζd・ζ(a+b)c
=αζac+bc+d=σ(ac)(bc+d)(αζ)
⇔ σcdσab=σ(ac)(bc+d) (mod 5)
単位元はσ10 で,σab の逆元はσa' (-a'b) です。ただし,aa'=1 (mod 5) 。
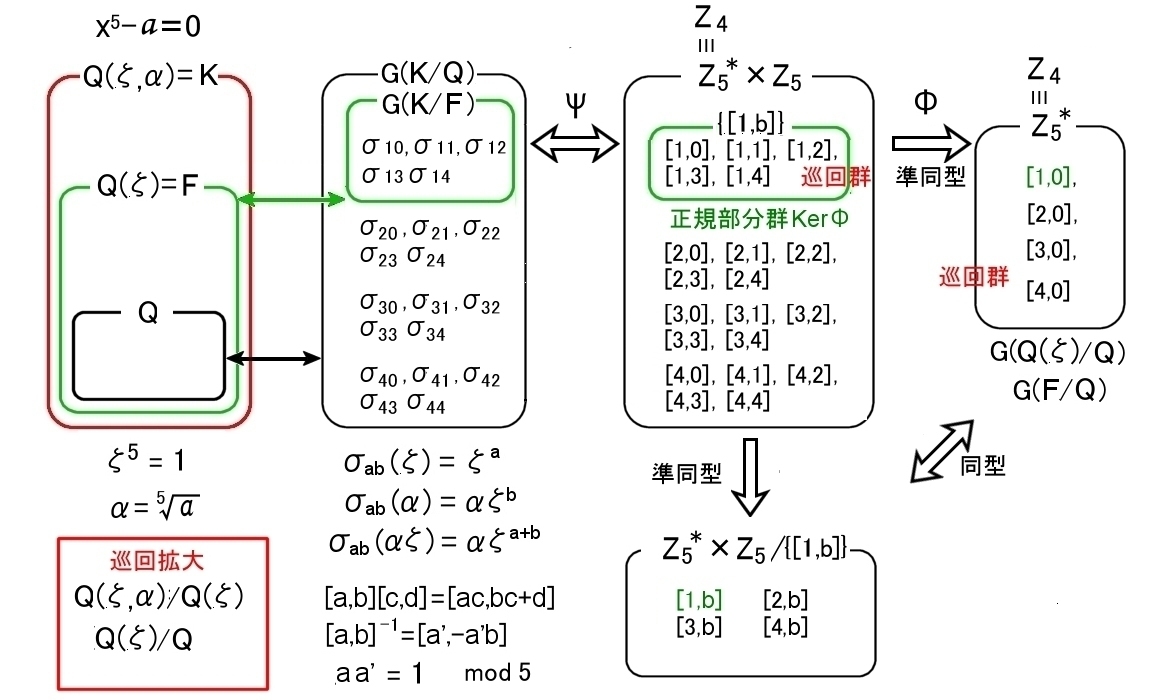
よって,ガロア群 G(Q(ζ,α)/Q)=G(K/Q)= {σ10,σ11,・・・,σ43,σ44 } の位数20の群で,群 Z5*×Z5 と同型であり,
Ψ: σab ⇔ [a,b] a∈ Z5*,b∈Z5
と対応させることができます。
[3]
Z5*×Z5 の乗法は,
[c,d] [a,b] =[ac,bc+d] ex. [2,4] [3,4]=[6,16]=[1,1]
で定義すれば,ガロア群の元σcdσab=σ(ac)(bc+d) の乗法に対応します。
単位元は[1,0]です。 [a,b] の逆元は [a',-a'b],aa’=1 (mod 5) です。
例えば,[2,4] の逆元は,[3,-12]=[3,3]です。 検算 [2,4] [3,3]=[6,15]=[1.0]
群 Z5*×Z5 の部分群として,{[1,b]} (b=0,1,2,3,4 ) を考えるとこれは正規部分群であり,巡回群 Z5 です。
実際,
[1,1] [1,1] =[1,2]
[1,1] [1,1] [1,1]=[1,1] [1,2]=[1,3]
[1,1]4=[1,4]
[1,1]5=[1,0]
と確かめられます。
また, {[1,b]} は,G(Q(ζ,α)/Q(ζ)) と同型であり,
|G(Q(ζ,α)/Q(ζ))|=5=| Z5|
となっています。 ( [σ1b] の元は Q(ζ) の元を動かさない。)
[4]
次に,Z5*×Z5 からその部分群 Z5*,つまり,[a,0] (a=1,2,3,4 ) の形の元への準同型写像Φを考えることができますが,
この像 Z5* は巡回群となっています。
[ Q(ζ):Q ]=4=φ(5) [拡大次数]
Gal ( Q(ζ):Q )≡(Z5)*
を確かめることができます。すると,
[Q(ζ,α):Q]=[Q(ζ,α):Q(ζ)] [Q(ζ):Q]=5×4=20
と,Q(ζ,α)/Q の拡大次数が計算できます。もちろん,これは G(Q(ζ,α)/Q)
のガロア群の位数と一致します。
[5]
例2 n=6 複合数の場合 x6ーa=0
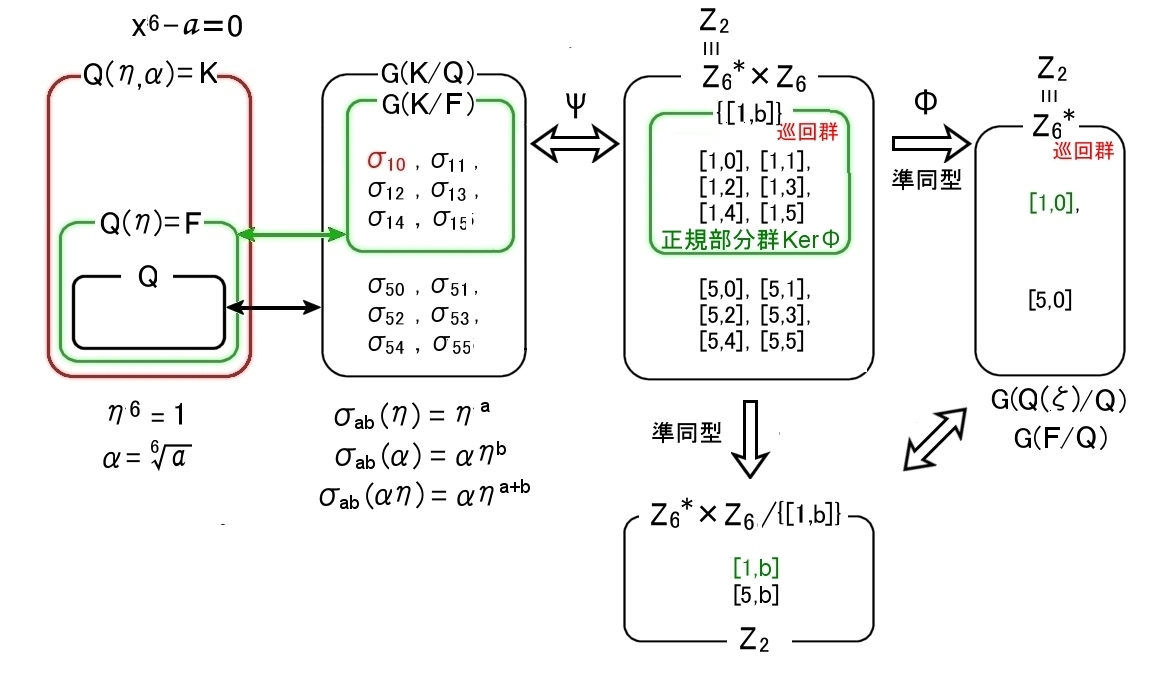
n=5 の場合からn=6 と変更するだけで同じ議論ができます。
Q上のK自己同型写像σab を次のように定義することができます。
σab(q)=q (q∈Q)
σab(η)=ηa (a=1,5 )
σab(α)=αηb (b=0,1,2,3,4,5 )
σab(αη)=αηa+b (mod 6)
|G(α,η)/Q|=12
a=1と制限すれば,F上のK自己同型写像は,G(Q(η,α)/Q(η))={σ10,σ11,σ12,σ13,σ14,σ15 } の6個で,これはZ6と同型な巡回群で,Q(η)=Fの元を動かしません。
群 Z6*×Z6 の正規部分群 [1,b] (b=0,1,2,3,4,5 ) を考えるとこれも巡回群 Z6 です。
Z6*は,Z6から零因子,2,3,4 を除いた 1,5 (mod 6) の元から成り立っています。
Z6*×Z6 から Z6* への写像
Φ: [a,b] → [a,0]
は準同型写像で,KerΦ=[1,b] で Z6*×Z6を除して得られる剰余群(Z6*×Z6)/[1,b]
[ Q(η):Q ]=2=φ(6) [拡大次数]
Gal ( Q(η):Q )≡(Z6)*
を確かめることができます。すると,
[Q(η,α):Q]=[Q(η,α):Q(η)] [Q(η):Q]
= 6 × 2 = 12
と,Q(η,α)/Q の拡大次数が求まります。これはガロア群の G(Q(η,α)/Q) の位数と一致します。
[6]
| 定理 体 Q に1の原始 n 乗根の一つζを添加した体を F=Q(ζ) とする。 また,xn−a の分解体をKとする。 このとき,二項拡大 K/Q ガロア群 G(K/Q) は可解群である。 |
クンマー拡大の定理と同内容のことを,可解群という用語で簡潔に言い直した定理です。
ガロア拡大体,ガロア群の関係を準同型定理を通して眺めていけば,自ずと浮かび上がってきます。
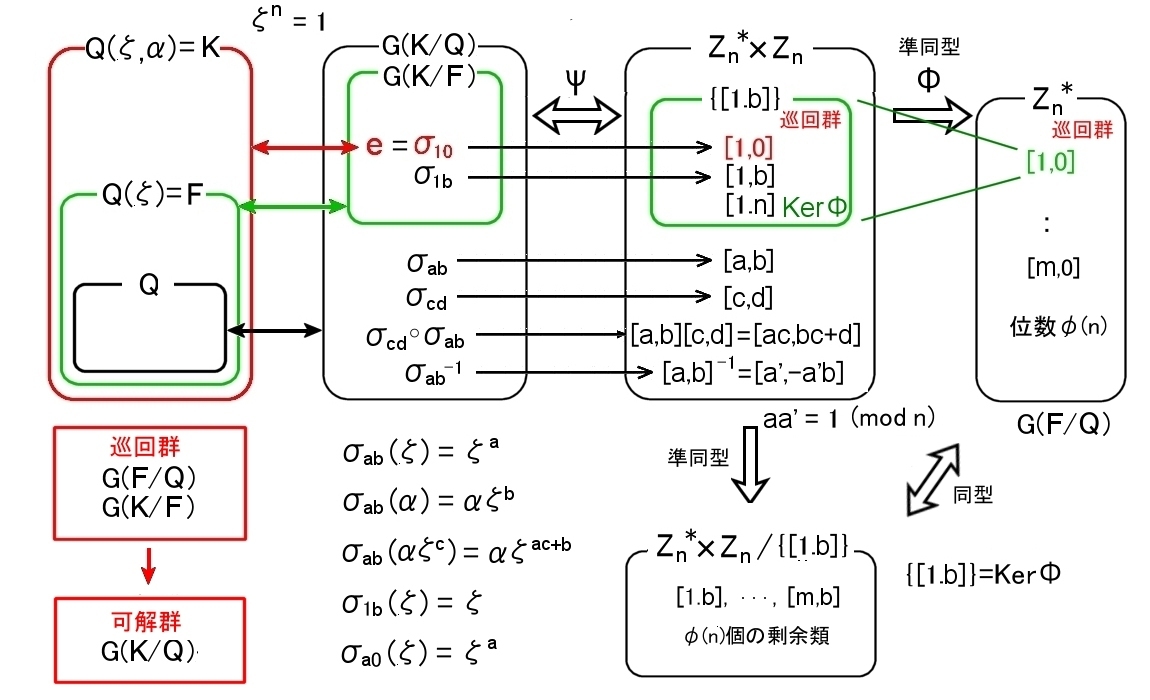
体Qからxn−a の分解体をKへのガロア拡大 K/Q の中間体Fを1のn乗根をQに添加した体とする。
G(K/F)はn次の巡回群になり,G(F/Q)はφ(n)次の巡回群になる。よってG(K/Q)は可解群,K/Qは巡回拡大
拡大次数は,
[Q(ζ,α):Q]=[Q(ζ,α):Q(ζ)] [Q(ζ):Q]
[K:Q] = [K:F] [F:Q]
= n × Φ(n)
| 定理 体 Q に1の原始 n 乗根の一つζを添加した体を F=Q(ζ) とする。また,K/F をガロア拡大,対応するガロア群 G(K/F) が巡回群であるとする。 そのとき,K は F の二項拡大体 [#] である。すなわち,a∈F が存在して,多項式 xn−a=0 の分解体が K となっている。 |
これは一つ前に示した定理の逆です。
定理の証明
(1) ガロア拡大 K/F に対応するガロア群を,
Gal(K/F) = { σ,σ2,・・・,σn-1,σn=e }
を元とする巡回群とする。
(2) ここで,c∈K に対するラグランジュの分解式 (〜のリゾルベント)と呼ばれる次式を定義する。
α=ζn-1σ(c)+ζn-2σ2(c)+・・・+ζσn-1(c)+e(c) ・・・ [*]
このとき,α≠0 となるように c ∈Kを選ぶ。 ⇒ 選べる理由 [#]
(3) σがFの元ζを動かさないことに留意して,σをこの両辺に繰り返し作用させれば,
σ(α)=ζn-1σ2(c)+ζn-2σ3(c)+・・・+ζσn(c)+σ(c)
=ζ{ζn-1σ(c)+ζn-2σ2(c)+ζn-3σ3(c)+・・・+e(c) }
=ζα
同様に計算して,
σ2(α)=ζ2α
・・・・・・
σk(α)=ζkα
となる。
(4) 一方,σ(αn)={σ(α)}n=(ζα)n=αn であるから,αn はσで動かない元で,F に属する。これを a=αn (∈F) とおくと,αはF上の二項式
xn−a
の根となっている。
(5) このとき,σk ∈Gal(K/F) はこれら共役根から共役根への自己同型写像であり,二項式 xn−a の共役根のすべては,
α,ζα,ζ2α,・・・,ζn-1α
で与えられる 。二項式 xn−a の分解体は F(α,ζα,ζ2α,・・・,ζn-1α)=F(α) であるが,これはFの拡大体 K となる。
[1]
|
定義 f(x) を体 Q 上の多項式とし,Q 上の f(x) の分解体を K とする。 K が Q からべき根拡大の繰り返し [累べき根拡大] によって得られるとき,方程式 f(x)=0 は,「べき根によって解ける」,または「代数的に解ける」という。 |
|
ガロアの定理 Q を (有理数) 体,f(x) を Q 上の多項式 ,f(x) の分解体を K とするとき, 「方程式 f(x)=0 が代数的に解ける。」 ⇔ 「f(x)
のガロア群 G(K/Q) が可解群である。」 |
証明
必要な材料は全部揃っている。だが,ガロアは決闘に出かけてしまった。
 |
| 生前最後の1枚。 あと4日だよ,にゃんぐろ君。 |
|
アーベル ー ルフィニの定理 Q 上の任意の方程式, f(x)=xn+a1xn-1+・・・+an=0 : ,ak∈Q (k=1,2,・・・,n) は,n≧5 のとき,代数的に解くことはできない。 |
反例を一つ挙げてもよいし,一般的な5次方程式のガロア群がS5であることを示してもよい。
|
補題
このとき,α≠0 となるように c を選ぶことができる。 |
背理法で証明する。
(1) F上のn次既約多項式の根の一つで,K=F(c) となる c ∈K を選ぶ。
[*] 式において,c → c,c2,c3,・・・,cn-1 とおくと,( 右辺だけ書くと )
c+ζn-1σ(c)+ζn-2σ2(c)+・・・+ζσn-1(c)
c2+ζn-1σ(c2)+ζn-2σ2(c2)+・・・+ζσn-1(c2)
c3+ζn-1σ(c3)+ζn-2σ2(c3)+・・・+ζσn-1(c3)
・・・・・
cn-1+ζn-1σ(cn-1)+ζn-2σ2(cn-1)+・・・+ζσn-1(cn-1)
さらに,
1+ζn-1+ζn-2+・・・+ζ ( =0 )
も追加して,これら多項式がすべて 0 であると仮定して矛盾を導く。
(2) 上のすべての式の値が 0 として,それらを行列で表すと,(↓ σn-1(ck)=σn-1(c)k を用いる。[#] )
1 1 1 ・・・ 1 1 = 0 c σ(c) σ2(c) ・・・ σn-1(c) ζn-1 0 c2 σ(c)2 (σ2(c))2 (σn-1(c))2 ζn-2 : : : : : : : : cn-1 (σ(c))n-1 (σ2(c))n-1 ・・・ (σn-1(c))n-1 ζ 0
(3) もし,左辺の正方行列に逆行列が存在すると,それを左辺から掛ければ,1,ζk=0 (k=1,・・・,n-1) と矛盾を生じるので,左辺の行列式は0でなければならない。すなわち,
Δ= 1 1 1 ・・・ 1 =0 c σ(c) σ2(c) ・・・ σn-1(c) c2 (σ(c))2 (σ2(c))2 (σn-1(c))2 : : : : : cn-1 (σ(c))n-1 (σ2(c))n-1 ・・・ (σn-1(c))n-1
(4) ところが,この行列式はVandermondeの行列式として知られていて,
Δ=Πj >k (σj (c)−σk(c))
と表せることが分かっている。
(5) ところが,自己同型写像は j≠k ならば,σj (c)≠σk(c) なので,Δ≠0 でなければならず,矛盾を生じる。
よって,c,c2,c3,・・・,cn-1 のいずれかを代入した [*] 式αは 0 とはならない。(終)
参考
|
Vandermondeの行列式
|