| Appendix1 位数 p-1 の元 (原始元) の存在 | ||
| f-denshi.com 最終更新日: 21/07/30 | ||
| [目次へ] | ||
| サイト検索 | ||
有限体には必ず原始元(原始根)が存在することの証明を示します。
| 定理 Fp* に原始根が少なくとも1つ存在すること ⇔ Fp* に位数 p-1 の元が少なくとも1つは存在する。 |
[証明の方針]
Fp* から1以外の元を取り a とし、aの位数 [#] を s とする。
(ケース1)
s=p-1 ⇒ 証明終わり
(ケース2)
s<p-1 ⇒ 「Fp* に位数が s より大きい元が存在する」・・・・・・・・・・・[*]
を示す。
[*] が成り立てば、
⇒ その元を s1(>s)とする、もし s1<p-1 なら、位数が s1 より大きい元が存在するはず、
その元を s2 とする、もし s2<p-1 なら、 位数が s2 より大きい元が存在する
以上、 sn=p−1 となるまで繰り返す → 定理は証明される。
[*] の証明
(1) a、a2、a3、・・・、as-1、as(=1) は互いに異なる。
(2) a、a2、a3、・・・、as-1、as(=1) は s 乗すると1になる。
(3) a、a2、a3、・・・、as-1、as(=1) は xs−1=0 の根のすべてである。
(4) a、a2、a3、・・・、as-1、as(=1) 以外の元 b が存在して,その位数 t と s の最小公倍数 を k とすれば、k > s である。
なぜならば,まず,a、a2、a3、・・・、as-1 以外の元 b が存在する。( s<p-1 なので )
(A) b の位数 t>s → [*]が成り立つ、証明終わり
(B) b の位数 t≦sの場合
s と t との最大公約数を d とし、
s=s’d, t=t’d
とすると,
ケース1
t が s の約数 (t’=1)のとき ⇒ bs=bs’d=(bt)s’=1
⇒ b は xs−1=0 の根である。 (矛盾)
ケース2
t が s の約数でない (t’≠1) であるとき ⇒ t と s の最小公倍数は,
k=s’t’d =t’s > s
を満たす。以上で,(4) が示された。
(5) すると,位数 k (>s) の元 c が存在する。
(6) 具体的には c=aS1bt1の位数がkであることを示す。
ただし、S1とt1を次のように定義される。
s (=s’d ) の約数のうちで t’と素で最大のものを S0 として、
s=S0S1
と書くと、S1は整数でS0とS1とは互いに素 (=1以外に約数を持たない。 )
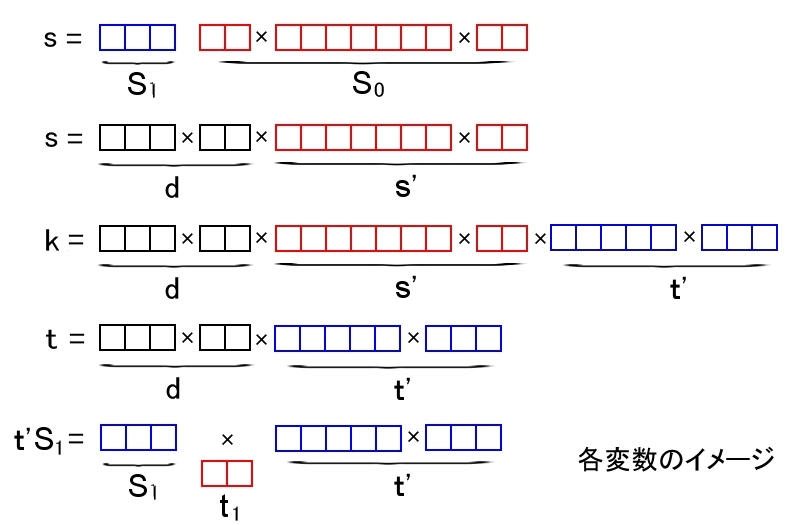
(7) また、s’は S0 の約数 ( s’≦S0 )
S1は d の約数 ( d≧S1 )
⇒ t’S1は t ( =t’d ) の約数
⇒ t=(t’S1)t1 なる整数t1が存在する。 (S0 はt’S1と互いに素でもある。)
(8) ここで,c の k 乗を計算してみる.と,
ck=(aS1bt1)k=aS1kbt1k=aS1t’sbt1t’s=(as)S1t’bt1t’S0S1
=(as)S1t’(bt)S0=(1)S1t’(1)S0=1
→ c の位数は k 以下である。
(9) 次に、cm=1 ならば、m≧k を示そう。
1=(cm)S0=(aS1bt1)mS0=aS0S1mbt1mS0=(aS)mbt1mS0=bt1mS0
よって、t(=t’S1t1)はt1mS0の約数、(かつ、S0 はt’S1と互いに素) → t’S1はmの約数
1=(cm)S1t’=(aS1bt1)mS1t’=aS1S1mt’bt1mS1t’=aS1S1mt’(bt)m=aS1S1mt’
よって、s(=S0S1)はS1S1mt’の約数、(かつ、S0 はS1とt’互いに素) → S0はmの約数
したがって、(t’S1)S0=k は m の約数 → m≧k