| Appendix5 3次,4次方程式の解の公式 | ||
| f-denshi.com 最終更新日: 04/11/8 | ||
| [目次へ] | ||
[1] 3次方程式の解法を紹介します。 有理数を係数とする3次方程式:
0 =x3+r2x2+r1x+r0 ・・・・・・・・・・・・・・・・・・・ (0)
は,x = (X−r2/3)と置き換えることで,2次の項のない3次方程式
0 =X3+pX+q ・・・・・・・・・・・・・・・・・・ (1)
に変換できます。したがって,この方程式(1)の解の公式を導けば十分です。
[2] 解法のポイントは次の2つの恒等式にあります。
[A] X3−y3−z3−3Xyz = X3−3yzX−y3−z3
[B] X3−y3−z3−3Xyz = (X−y−z)(X−ωy−ω2z)(X−ω2y−ωz)
ここで,ωは1の原始3乗根,すなわち,
ω =exp [2πi /3]=
−1+i 3 2
で,ω3 = 1, ω2+ω+1 = 0 を満たします。
[3] まず,[A] ですが,これは(1)と比較すれば,
p = −3yz ・・・・・・・・・・・・・・・・・・・・・・・ (2)
q = −y3−z3 ・・・・・・・・・・・・・・・・・・・・・・・ (3)
が成り立つときに方程式(1)の右辺に等しいことが見て取れます。
[4] 一方,[B]は
(X−y−z)(X−ωy−ω2z)(X−ω2y−ωz) = 0
とおいて,X の方程式とみなせば,その根が,
y+z
ωy+ω2z
ω2y+ωz・・・・・・・・・・・・・・・・・・・・・・・ (4)
の3つであることを示しています。
[5] つまり,未知数 y,z の連立方程式(2),(3)の解がわかれば,それを(4)に代入して,3次方程式(1)の一般解が得られるわけです。この連立方程式解は簡単に次のように求まります。(2)を両辺3乗して 27 で割れば,
p3/27 = −y3z3 ・・・・・・・・・・・・・・・・・・・・・・ (5)
(5)と(3)から, y3 と z3 とは次の T に関する2次方程式の解であることがわかります。
T2−(y3+z3)T+y3z3 = T2+qT−(p3/27) = 0 ・・・ (6)
したがって,2次方程式の解の公式から(6)の2つの根を求め,立方根をとれば,
y =
−q+ D 1/3 =
−(q/2)+ (q/2)2+(p/3)3 2
z =
−q− D 1/3 =
−(q/2)− (q/2)2+(p/3)3 2
ただし,判別式: D = q2+4(p3/27)
が得られます。この y,z を(4)に代入した次式が,3次方程式(1)の3つの解です。
−(q/2)+ (q/2)2+(p/3)3 +
−(q/2)− (q/2)2+(p/3)3
ω
−(q/2)+ (q/2)2+(p/3)3 +ω2
−(q/2)− (q/2)2+(p/3)3
ω2
−(q/2)+ (q/2)2+(p/3)3 +ω
−(q/2)− (q/2)2+(p/3)3
[蛇足]
[B]の式はよく見かける公式
X3+y3+z3−3Xyz = ( X+y+z )( X2+y2+z2−Xy−yz−zX )
= ( X+y+z )( X+ωy+ω2z )( X+ω2y+ωz )
にて,y → - y, z → - z と置き換えたものです。
[1] 3次方程式の解法と同様に有理数を係数とする4次方程式:
0 = x4+r3x3+r2x2+r1x+r0 ・・・・・・・・・・・・ (0)
も x = (X−r3/4)と置き換えることで,3次の項のない4次方程式:
0 = X4+pX2+qX+r ・・・・・・・・・・・・・・・・ (1)
に変換できます。したがって,一般の4次方程式の解として,この方程式(1)の解の公式を導けば十分です。
[2] ポイントは次の2つの恒等式にあります。(↓ 3次方程式の場合とよく比べてください)
[C] X4+y4+z4+w4−2(X2y2+X2z2+X2w2+y2z2+y2w2+z2w2)−8Xyzw
= X4−2(y2+z2+w2)X2−8yzwX+[y4+z4+w4−2(y2z2+y2w2+z2w2)]
= X4−2(y2+z2+w2)X2−8yzwX+[(y2+z2+w2)2−4(y2z2+y2w2+z2w2)]
( X の方程式とみなせるようにXだけわざと大文字にしています。)
[D] X4+y4+z4+w4−2(X2y2+X2z2+X2w2+y2z2+y2w2+z2w2)−8Xyzw
= (X−y−z−w)(X−y+z+w)(X+y−z+w)(X+y+z−w)
[3] まず,[C] を X の方程式とみて,
p = −2(y2+z2+w2) ・・・・・・・・・・・・・・・・・・・ (2)
q = −8yzw ・・・・・・・・・・・・・・・・・ (3)
r = (y2+z2+w2)2−4(y2z2+y2w2+z2w2) ・・・・・・・・ (4)
とおけば,4次方程式(1)の右辺に等しくなります。
[4] 次に[D] は
0 = (X−y−z−w)(X−y+z+w)(X+y−z+w)(X+y+z−w)
を X の方程式とみなせば,その4つの解 x1,x2,x3,x4 は,
x1=+y+z+w
x2=+y−z−w
x3=−y+z−w
x4=−y−z+w・・・・・・・・・・・・・・・(5)
で与えられることを示しています。つまり,未知数 y,z,w の連立方程式(2),(3),(4)を解いて,その解を(5)に代入して得られる 4つの値が 4次方程式の解なのです。
[5] さて,連立方程式(2),(3),(4)を
y2+z2+w2 = −p/2
y2z2w2 = (q/8)2
y2z2+y2w2+z2w2 = [(y2+z2+w2)2−r ]/4 = p2/16−r/4
と変形すれば,y2,z2,w2 は次の3次方程式の3つの解になっていることがわかります。
(T−y2)(T−z2)(T−w2) = T3−(y2+z2+w2)T2+(y2z2+y2w2+z2w2)T− y2z2w2
= T3+(p/2)T2+(p2/16−r/4)T−(q/8)2
= 0
先ほど示したように3次方程式の解は公式によって必ず求まりますから,それらを t1,t2,t3 としましょう。すると,
y = ±
t1 , z = ±
t2 , w = ±
t3
と表せるはずです。 y,z,w としてどのように複合 +,− を選択するかは,q = −8yzw を満たすように決定できます。一組の y,z,w が定まれば,(5)より4次方程式の解が求まります。
[蛇足]
[D] X4+y4+z4+w4−2(X2y2+X2z2+X2w2+y2z2+y2w2+z2w2)+8Xyzw ←M78さんに間違いを教えていただきました。
=(X+y+z+w)(X+y−z−w)(X−y+z−w)(X−y−z+w)
4次方程式のガロア対応
4次方程式
X4+pX2+qX+r=0
(X−x1)(X−x2)(X−x3)(X−x4)=0
(X−y−z−w)(X−y+z+w)(X+y−z+w)(X+y+z−w)=0
| 2 | 3 | 2 | 2 | 位数=拡大次数 | ||||||
| Gi/Gi+1 | ガロア群 | S4/A4 | A4/H | H/N | N/{e} | Gal(Fi+1/Fi) | ||||
| Gi= | S4 | ⊃ | A4 | ⊃ | H | ⊃ | N | ⊃ | E | 部分群 (固定群) |
| ガロア対応 | ||||||||||
| Fi= | Q | ⊂ | Q((y2-z2)(z2-w2)(w2-y2)) | ⊂ | Q(y2,z2,w2) | ⊂ | Q(y2,z2,w) | ⊂ | Q(y,z,w) | 中間体 (固定体) |
| Fi+1/Fi | Q((y2-z2)(z2-w2)(w2-y2))/Q Q(y2,z2,w2)/Q((y2-z2)(z2-w2)(w2-y2)) Q(y2,z2,w)/Q(y2,z2,w2) Q(y,z,w)/Q(y2,z2,w) 最小分解体 | ガロア拡大 | ||||||||
| Q(y2,z2,w2)/Q [6次拡大] | ||||||||||
| 3次方程式 | 2次方程式 | 2次方程式 | ||||||||
| T3+(p/2)T2+(p2/16−r/4)T−(q/8)2 (T−y2)(T−z2)(T−w2) =0 |
R2−w2=0 (R+w)(R−w)=0 |
R2−z2=0 |
方程式 | |||||||
|
p=−2(y2+z2+w2) |
x1=+y+z+w x2=+y−z−w x3=−y+z−w x4=−y−z+w |
Q(y,z,w)=Q(x1,x2,x3,x4) | 補足 | |||||||
・同型写像の定義
|
|
恒等写像も含めて,この写像は4次方程式の解を並び換えている。
・各中間体を動かさない固定群(=S4の正規部分群)を見つけるための表
| 中間体 | Q | Q((y2-z2)(z2-w2)(w2-y2)) | Q(y2,z2,w2) | Q(y2,z2,w) | Q(y,z,w) | ||||||||||||
| m= | p | q | r | (y2-z2)(z2-w2)(w2-y2) | y2 | z2 | w2 | y2 | z2 | w | y | z | w | ||||
| e(m)= | p | q | r | (y2-z2)(z2-w2)(w2-y2) | y2 | z2 | w2 | y2 | z2 | w | y | z | w | ||||
| h1(m)= | p | q | r | (y2-z2)(z2-w2)(w2-y2) | y2 | z2 | w2 | y2 | z2 | w | -y | -z | w | ||||
| h2(m)= | p | q | r | (y2-z2)(z2-w2)(w2-y2) | y2 | z2 | w2 | y2 | z2 | -w | -y | z | -w | ||||
| h3(m)= | p | q | r | (y2-z2)(z2-w2)(w2-y2) | y2 | z2 | w2 | y2 | z2 | -w | y | -z | -w | ||||
| α(m)= | p | q | r | (y2-z2)(z2-w2)(w2-y2) | z2 | w2 | y2 | z2 | w2 | y | z | w | y | ||||
| σ(m)= | p | q | r | -(y2-z2)(z2-w2)(w2-y2) | z2 | y2 | w2 | z2 | y2 | w | z | y | w | ||||
| 固定群 | S4 | A4 | H | N | E | ||||||||||||
| A4∪σA4 | <e,h1,h2,h3,α> | {e,h1,h2,h3} | {e,h1} | {e} | |||||||||||||
青い背景の体の元(の組)は,左端に示した群の元の働きで動かない。
p=−2(y2+z2+w2)
q=−8yzw
r=y4+z4+w4−2(y2z2+z2w2+w2y2)
S4 :<h1,h2,h3,α,σ>=A4∪σA4 (4文字対称群)
A4 :<h1,h2,h3,α>={e,hx,hy,hz,a1,b1,a2,b2,a3,b3,a4,b4} (4文字交代群)[#]
H :<h1,h2,h3> = {e,h1,h2,h3}
N :<h1> = {e,h1}
E : {e}
注意: 正四面体群において用いた元の記号とは,h1⇔hy,h2⇔hx,h3=hz,α⇔a1 と対応させ,σは任意の互換,たとえば,(12)と考えればよい。
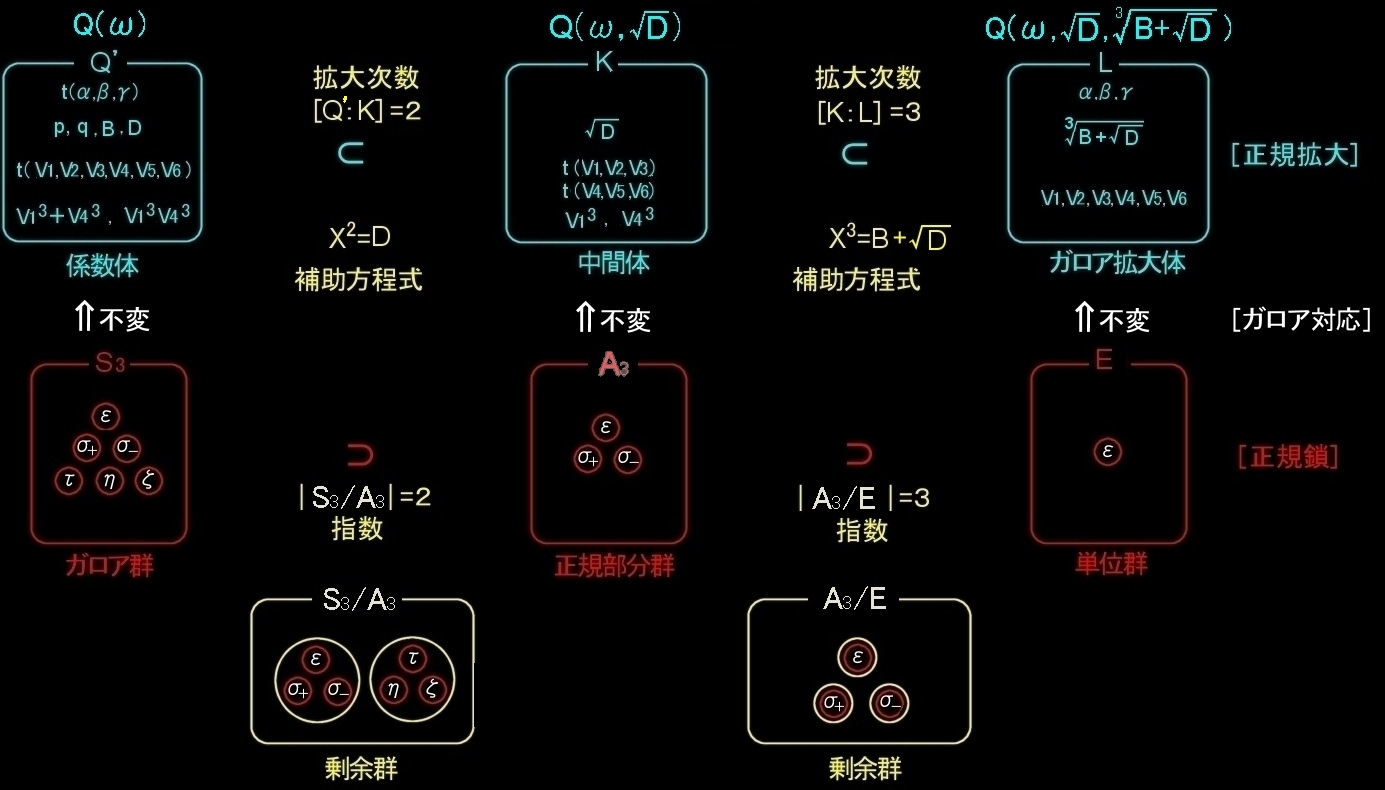
メモ書き: 一般の3次方程式のリゾルベントを用いた解法におけるガロア群とガロア拡大体との関係 (概略)
有理数体Q上の一般3次方程式を加減乗除とべき根で解くことを考える。(べき根で表現可能な1の3乗根ωは予めQに添加してQ’としておく。)
x3+0・x2+p・x+q=0, p,qは有理数
解と係数の関係は対称式で次のように書ける。
0=−(α+β+γ)
p=αβ+βγ+γα
q=−αβγ
ここでは,体を累次拡大することで解が得られるもっとも複雑な場合を想定して話を進める。まず,対称式,t(α,β,γ) [#]は,根α,β,γの置き換え,3文字の置換(3次対称群)によって変化しない。したがって,
α,β,γの置換を行っても係数 0,p,q (係数体)は不変である。当たり前。
一般3次方程式のガロア群は3次対称群 S3={ε,σ+,σ-,η,ζ,τ}を具体的に書き下すと次のとおりである。
|
正規部分群 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
天下り的であるが,3つの解とωから作られるラグランジュのリゾルベント(分解式)と呼ばれる次式 V,
|
c.f. |
|
を定義する。6つの置換を V=V1 にそれぞれ作用させると,以下のとおり置換ごとに異なる6つの式,V1,V2,V3,V4,V5,V6 が得られる。
置換 変換前
の値
⇒F(V)変換後 値 多項式 (F(α,β,γ)) 記号 ε V ⇒ε(V) =V1 =γ+αω+βω2
=V σ- V ⇒σ-(V) =V2 =β+γω+αω2 =Vω σ+ V ⇒σ+(V) =V3 =α+βω+γω2 =Vω2 η V ⇒η(V) =V4 =γ+βω+αω2 =W ζ V ⇒ζ(V) =V5 =α+γω+βω2 =Wω τ V ⇒τ(V) =V6 =β+αω+γω2 =Wω2
さらに,V2,・・・,V6 ついて置換を作用させた結果は以下のとおりとなる。
x= V1 V2 V3 V4 V5 V6 ε(x)= V1 V2 V3 V4 V5 V6 σ-(x)= V2 V3 V1 V5 V6 V4 σ+(x)= V3 V1 V2 V6 V4 V5 η(x)= V4 V5 V6 V1 V2 V3 ζ(x)= V5 V6 V4 V3 V1 V2 τ(x)= V6 V4 V5 V2 V3 V1
すなわち,S3の元は,L3={V1,V2,V3,V4,V5,V6 }に対する自己同型写像となっている。
Vj の性質 (証明略)
(1) L=Q(α,β,γ)=Q(V1)=Q(V2)=Q(V3)=Q(V4)=Q(V5)=Q(V6) [単項拡大]
(2) S3を作用させて得られる6つのVjからなる対称式t(V1,V2,V3,V4,V5,V6)はS3によって不変(Vj 上の自己同型写像)
⇒Q’に属する。()
(3) V3=V・Vω・Vω2=V1V2V3,および,W3=V4V5V6
(4) α,β,γはVj の整式で表される。
具体的には,
α= 1 (Vω2+Wω) 3
β= 1 (Wω2+Vω) 3
γ= 1 (V+W) 3
つまり,
Vがp,,qの加減乗除とそれらの冪根で表されれば,方程式の解の値もべき根で表される。
当初の3次方程式の解をべき根で表すという問題は,ωを導入したことで,「Vをべき根で表す」という問題に置き換えられたのだ。
そこで,Vj =V,Vω,Vω2,W,Wω,Wω2 を根とするQ(ω)上の6次方程式,
(x−V)(x−Vω)(x−Vω2)(x−W)(x−Wω)(x−Wω2)=0
を考える。これを展開すると,
=(x3−V3)(x3−W3)
=x6−(V3+W3)x3+V3W3 =0
ここで,X≡x3 とおくと,Xに関する2次方程式とみなせる。また,その2次方程式の係数である,
V3+W3,および,V3W3 は,α,β,γの置換を行っても不変 (V1,V2,V3,V4,V5,V6に置換を行っても不変) であるから,Q’の数である。⇒[#]
具体的には,V=γ+αω+βω2,W=γ+βω+αω2を代入して,
V3+W3 = 27αβγ =−27q
V3W3 =−27(αβ+βγ+γα)3 =−27p3
すなわち,V3+W3,および,V3W3 はQ’に属する。よって,XのQ’上(Q上でも同じ)の2次方程式を解いて,
X=V3または,W3 ←この解を係数体Q’に添加した拡大体が中間体になっている。
を解として求めることができる。
その補助方程式を具体的に書くと,
X2+27qX−27p3 =0
これを解くと,
V3,W3 =
− 27q ± 2
27q 2 +27p3 2
ここで,
B=− 27q 2
D≡ 27q 2 +27p3 [2次方程式の判別式] 2
とおき,および,複号はV3に対して+,W3に対して,−を与えることにする。(ガロア拡大においてはどちらかひとつ添加すればよい。)
さらに,それぞれの立方根をとれば,VとWが係数p,qを用いた形で求まる。
V=
B+
D , W=
B−
D
したがって,3次方程式の解はこれらを,
α= 1 (Vω2+Wω) 3
β= 1 (Wω2+Vω) 3
γ= 1 (V+W) 3
に代入すれば,本文中と同じ結果を得る。例えば,
γ= 1
− 27q + 2
27q 2 +27p3 2 +
− 27q − 2
27q 2 +27p3 2 3
=
−(q/2)+ (q/2)2+(p/3)3 +
−(q/2)− (q/2)2+(p/3)3
ガロア群の性質トリゾルベントについて追加説明:
固定部分群と中間体との対応を見るために自己同型写像として,S3の元がリゾルベントに働く様子を示す。
自己同型
写像中間体 Q(ω) Q(ω, V3) Q(ω, V3,V) x= V3+W3 V3W3 V3 W3 V W S3 A3 ε(x)= V3+W3 V3W3 V3 W3 V W σ-(x)= V3+W3 V3W3 V3 W3 V2 V5 σ+(x)= V3+W3 V3W3 V3 W3 V3 V6 η(x)= V3+W3 V3W3 W3 V3 V4 V1 ζ(x)= V3+W3 V3W3 W3 V3 V5 V3 τ(x)= V3+W3 V3W3 W3 V3 V6 V2
青い背景の部分は自己同型写像によって体の元が動かないことを示す。
Q(ω)を不変とするのは,S3である。
Q(ω,V3)を不変とするのはS3の部分群A3である。
Q(ω, V3,V)を不変とするのは単位元εだけからなる部分群Eである。
正規部分群A3の性質
| A3 | t(V1,V2,V3) | t(V4,V5,V6) | ||||||||||||||||||
| ε | V1→V1 V2→V2,V3→V3 |
V4→V4 V5→V5,V6→V6 |
||||||||||||||||||
| σ- |
|
|
||||||||||||||||||
| σ+ |
|
|
正規部分群C3による置換によって,V1,V2,V3の対称式,t(V1,V2,V3)と,V4,V5,V6の対称式,t(V4,V5,V6) は不変となっている。
(S3〜D3は同型。σ+とηとで生成される。)
[] 特に対称式,
V3=V1V2V3 および,W3=V4V5V6 はA3によって不変
V3=V13=V23=V33
W3=V43=V53=V63
一方,ηA3の置換によって,t(V1,V2,V3)とt(V4,V5,V6) とは交換される。
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| S3の軌道 | 剰余群表 |
一方,S3はV1,V2,V3,V4,V5,V6 の対称式を不変とする。
具体例はこれらを根に持つ多項式から作れる。
(x−V)(x−Vω)(x−Vω2)(x−W)(x−Wω)(x−Wω2)
の係数から出てくる対称式,
V3+W3,および,V3W3
はQ’上で不変であり,p,qで表せることはすでに示したとおり。
一つの図にまとめると次のとおり。