| 2 固有値の幾何学的意味 | ||
| f-denshi.com [目次] 最終更新日: 04/09/30 | ||
| サイト検索 | ||
ここでは線形代数において,固有値,固有ベクトルなるもの考える重要性を視覚的に理解するために,2次元ユークリド空間上のベクトルを例にとり,線形写像によってどのように変換されるのか具体的に見てみましょう。
結論を一言で言うと,”ほとんど” の線形写像はベクトルの”引き伸ばし(倍率が1以下ならば縮小)”と考えることができ,その引き伸ばしの方向を決めているのが固有ベクトルで倍率が固有値です。ただし,この様子は実数の世界で完全に捉えることは不可能で,複素数の世界において可能となります。
[1] まず,線形写像:
T(r ):r → v ( v =Tr )
を表す行列Tが対角行列で表せるとき,この写像が幾何学的にどのような意味をもつのか考えて見ましょう。
[ケース1] T(r)を表す行列を,
T = 2 0 0 3
としましょう。すると,標準基底:{ex,ey},
ex = 1 , ey = 0 0 1
をTの右からかけて,
Tex = 2 0 1 = 2 = 2ex 0 3 0 0
Tey = 2 0 0 = 0 = 3ey 0 3 1 3 ・・・・・・・ [*]
 なる関係があることがすぐに確かめられます。このとき,任意のベクトル,
なる関係があることがすぐに確かめられます。このとき,任意のベクトル,
r =xex+yey について
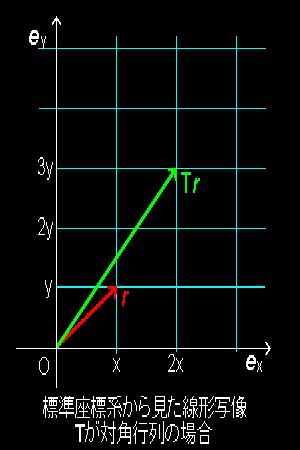
v =Tr =T(xex+yey)= xTex+yTey =(2x)ex+(3y)ey または,Tr = 2 0 x = 2x : 基底 {ex,ey} 0 3 y 3y
が成り立ちます。これからこの写像は,
x軸(ex )方向に2倍: ( x → 2x )
y軸(ey )方向に3倍: ( y → 3y )
に拡大する写像であることがわかります。つまり,線形写像:T(r):r → v を,
「ベクトルの各基底の方向への引き伸ばし」
として捉えることができます。この様子は右上図のように幾何学的に捉えることが可能です。
[ケース2]
[2] さて,今度は非対角成分が 0 でない値を持つ次のような線形写像の表現行列を考えて見ましょう。
T = 8 -2 3 1
今度は標準基底を使って写像の様子を計算をしみても [*] のような簡単な性質は見出せません。しかし,標準基底以外の基底:{u1,u2}をうまく探してやれば,[*] と同じように,
Tu1=λ1u1
Tu2=λ2u2
なる関係が成り立つかもしれません。 ←ケース1の Tex=2ex,Tey=3ey のような形に強引にもっていくわけです!
そこで,方程式:
Tu=λu ⇔ (T−λE)u = 0
成分で次のように書いて,
| 8 | -2 | x | = λ | x | ⇔ | λ−8 | 2 | x | = | 0 | ; u = | x | ||||||||||||||||
| 3 | 1 | y | y | -3 | λ−1 | y | 0 | y | ||||||||||||||||||||
を満たすように λ,u を求めてみましょう。これは連立1次方程式:
(λ−8)x+2y = 0
-3x+(λ−1)y = 0
の x=y=0 以外の解を求めることと同じです。その条件は,|T−λE|= 0,すなわち,
(λ−8)(λ−1)−2・(-3) = (λ−2)(λ−7) = 0
となります。したがって,λ= 2,7 であることが必要です。
λ=7 のとき,連立方程式は ← 連立1次方程式の話はこちらの講義で⇒ [#]
-x+2y=0,
-3x+6y=0
で,その解は任意実数を t として,
u1 = t 2 ,このとき,Tu1 = 7u1 ・・・ (1) 1
と求められます。
 |
| ( t=s=1 として, u1軸, u2軸を図示している。) |
λ=2 のとき連立方程式は
(2−8)x+2y = -6x+2y = 0
-3x+(2−1)y = -3x+y = 0
で,その解は任意実数を s として,
u2 = s 1 ,および,Tu2 = 2u2 ・・・ (2) 3
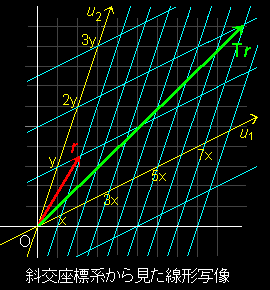
したがって,任意のベクトルをこの{u1,u2 }を基底に用いて,r = xu1+yu2 と表すことすれば,線形写像: T(r):r → v は,
v =Tr =T(xu1+yu2)=xTu1+yTu2 = 7xu1+2yu2
と計算できることになります。
[3] この様子は斜交座標として,{u1,u2 } を基底に用いれば,[ケース1]と同様に写像 T を,
u1軸(u1)方向に 7 倍: x → 7x
u2軸(u2)方向に 2 倍: y → 2y
「ベクトルの各基底の方向への引き伸ばしとして捉えることができる。」ことを意味しています。成分で表記すると,
Tr = 7 0 x = 7x :基底 {u1,u2 } 0 2 y 2y
と対角行列を使って書くことが可能です。ただし,ここでは,表現行列 T もベクトル r も基底 {u1,u2 } で表されていることに注意が必要です。
補足
上のちゃんとした計算は,(1),(2)は,
u1=t 2 = 2tex+tey 1
u2=s 1 = sex+3sey 3 より,基底変換の行列Pは,
P= 2t s ; P-1 = (1/5st) 3s -s t 3s -t 2t となります[#]。したがって,
T'= P-1TP = (1/5st) 3s -s 8 -2 2t s = 7 0 -t 2t 3 1 t 3s 0 2
このようにうまく基底を選び直して(=基底変換をおこなって),Tの行列表現を対角行列に変換することを対角化といいます。ここで,λの値(λ1,λ2) を行列 T の固有値,新しい基底ベクトルu1,u2 を固有ベクトルと言います。
(正確な定義は後で ⇒ [#] )
[ケース3]
[4] 次に回転行列と呼ばれる次のような行列要素で表される線形写像について考えて見ましょう。
T = cosθ -sinθ sinθ cosθ
この行列はよく知られているように2次元平面上のベクトルを回転させる行列です。[ケース2]の場合と同じように方程式:
Tu = λu ⇔ (T−λE)u=0 を満たすλ,u を求めると,
| cosθ | -sinθ | x | =λ | x | ⇔ | λ−cosθ | sinθ | x | =0 | ||||||||||
| sinθ | cosθ | y | y | −sinθ | λ−cosθ | y |
より, λ2−(2cosθ)λ+(cos2θ+sin2θ)=0 を解いて,
λ=cosθ±i sinθ (i は虚数単位)
固有ベクトルは,
u1 = t i で, Tu1 = (cosθ+i sinθ)u1 1
u2 = s 1 で, Tu2 = (cosθ−i sinθ)u2 i
と求められます。 r = xu1+yu2 とすれば,
Tr = T(xu1+yu2) = xTu1+yTu2 = (cosθ+i sinθ)xu1+(cosθ−i sinθ)yu2
と書けます。複素数が現れますが,そのみかけは[ケース2]と同じなので,写像 T は,基底{u1,u2 }を用いて,
u1軸(u1)方向に (cosθ+i sinθ) 倍: x → (cosθ+i sinθ)x
u2軸(u2)方向に (cosθ−i sinθ) 倍: y → (cosθ−i sinθ)y
と述べることができます。この結果は,「 ベクトルの各基底の方向への各倍率での引き伸ばし 」と形式的に述べることが可能です。ただし,斜交座標の基底であるu1,u2 は複素ベクトル空間 C2 上のベクトルで,[ケース1],[ケース2]と違って,この様子は残念ながら ”4次元空間” にしか描くことはできません。行列成分がすべて実数であっても固有値,固有ベクトル成分が実数とは限らないのでこのようなことがおこります。
[5] もう一つ注意を要するのは複素数の ”かけ算” の幾何学的な意味が実数のかけ算とは幾何学的に異なった見え方をするということです。複素数を成分とするベクトル空間を考えているときは,x を c =R(cosθ+i sinθ)倍するとは,ガウス平面に表した数 x を,
x の大きさを R 倍 して,
x の方向 を θ 回転させる
ことだからです。複素数,複素関数の基本的な性質はこちらにまとめてあります。 ⇒[#]
[ケース4]
[6] 最後の例は, ”これまで述べてきたようにすべてがうまくいくわけではない” という教訓のための問題です。
行列,
(1) T = 3 1 ; (固有多項式=0): (λ-3)(λ−1)+1=(λ−2)2=0 -1 1
の固有値は 2 で,固有値はこの1つしか存在しません。 固有ベクトルも
(2−3)x−y=0, x+(2−1)y=0 ⇒ : u = 1 -1
とひとつしか存在しません。 したがって,これまでのように対角化することはできないのです。
[7]この行列のみかけ(成分の並び方や正則性[#]など)はケース2や3に較べてあまり違いがありません。しかし,行列を対角化しようとすると,大きな違いが生じています。
正方行列はどのようなときに対角化可能で,どのようなときには対角化不可能なのでしょうか。次章から,しばらくこの問題の答えを探っていきましょう。