| 9-1 射影演算子 | ||
| f-denshi.com [目次] 最終更新日: 書き直し中 | ||
| サイト検索 | ||
ベクトルの内積,直交性を調べるためのツールを充実させておきましょう.
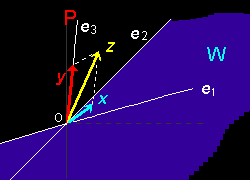
[1] 直和分解の特別な場合として直交分解というのがあります。ユニタリ空間 V の部分空間 W が与えられたとき,次の集合,
W⊥ = {y|内積(y,x )= 0, x ∈W ,y ∈V } [ 直交補空間 ]
を W の直交補空間といい,このW⊥もV の部分ベクトル空間[#]となっています。 また,このときユニタリ空間 V はW と W⊥の直和 [#],
V = W W⊥
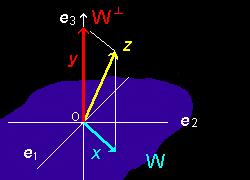
にもなっています。 すなわち,任意のベクトルz ∈V に対して,x ∈W ,y ∈W⊥ が存在し,
z =x +y
と一意的に表すことができます。
(直和分解の場合[#]は,x とy が一意的であることだけが必要で,これらが互いに直交している必要はありません。直交分解は直和分解の特別な場合です。)
 |
 |
||||
|
直交分解:V =W⊥W⊥ |
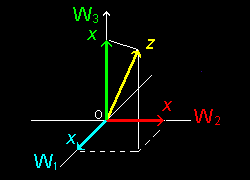
[2] このようなユニタリ空間 V の分割を部分空間に対して繰り返えしおこなうと,
V = W1 W2 ・・・・ Wm
というようにV はいくつかのお互いに直交する部分空間の直和で表すことができますが,これをユニタリ空間 V の直交分解と言いい,
V = W1⊥W2⊥・・・・・⊥Wm
という記号を用いて表します。このとき,V の任意のベクトルx について,
x =x1+x2+・・・+xm
ただし,
と表すことができます。もちろん,
n = dimV =dimW1+dimW2+・・・+dimWm
= s + t + ・・・ + u
が成り立っています。
|
補足: |
[1] ユニタリ空間 V が
V = W1⊥W2⊥・・・⊥Wm
と直交分解されているとき,V 上の任意のベクトルは,
x = x1+・・・xk+・・・+xm ( ただし,xk∈Wk )
と一意的に表されます。 このとき,x に作用して,ベクトルxk∈Wk を取り出す写像:
Pk: x → xk
を射影演算子(または,射影作用素)と言います。 射影演算子はV上の線形演算子であって,Wk の基底を { es+1,・・・,es+t }とすれば次のように内積( , )を用いて,
=xs+1es+1+・・・+xs+tes+t
=(x,es+1)es+1+・・・+(x,es+t)es+t [ 射影演算子 ]
と書くことができます[#]。
[2] この演算子について次の関係式が成り立ちます。
| 公式 射影演算子の基本的性質 (1) PjPk=O ( i≠j ) [ゼロ演算子≡O ] |
(証明)
(1) PjPkx =Pjxk =0 =Ox ( i≠j )
(2) Pj2x = Pj(Pjxj) = Pjxj = xj = Pjx
(3) (P1+・・・+Pk+・・・+Pm )x = P1x +・・・+Pkx +・・・+Pmx
= x1 +・・・ + xk +・・・+xm = x
=Ex
(4) P1 を次のような W1 への射影演算子として,
x = x1+x2, y = y1+y2, P1x = x1 ,P1y = y1
以下の内積を (xj,yk )=0, j ≠ k に注意して計算してみると,
(P1x,y ) = (x1,y1+y2 )=(x1,y1 )= (x1+x2,y1 ) = (x,y1 )
= (x,P1y )
ところが,(P1x,y ) = (x,P1*y ) でもある[#] ので,すぐ上の結果と比較すれば,P1*y =P1y ,すなわち,
P1*=P1 (終)
一般に,T = T* のような性質をもつ線形演算子をエミルート演算子と言い,後ほど詳しく説明します。