４　行列の対角化が可能な条件
f-denshi.com    ［目次へ］ 最終更新日:　21/08/30　　　図を追加
サイト検索

１．固有空間による直和

［１］　いよいよ，２．の懸案事項であった「行列が対角化可能であるための条件」を求めます。まず，「対角化可能」の厳密な定義から。

とします。ここで，Pはベクトル空間Vの基底変換の行列 [#]です。対角可能とは，「うまく基底を選びなおしてやる，つまり座標変換してやる[#]ことで，V上の線形写像の表現行列を対角行列にできる」ことを言うのです。

一般的に，基底の変換を相似変換といい，「T と D とは相似である」といいます。この用語は D が対角行列でない場合でも用いられます。

ここで，相似の意味は，「基底の取り方が違うだけ（＝成分を並べた表現行列が違って見えるだけ）で数学的な内容 (＝線形写像として) は同じだ」ということです。　　

［２］　いま，Tの固有多項式を，

Φ_T(λ)＝(λ−λ₁)^d₁(λ−λ₂)^d₂ ･･･ (λ−λ_m)^d_m　

とします。すなわち，異なる λ₁，λ₂，･･･，λ_m　の固有値をもち，それぞれの重複度は，d₁，d₂，･･･，d_m　であるとします。

この記号，用語のもとで，これから証明すべき定理を述べると，

つまり，各固有値に対して，その固有空間の次元とその固有値の重複度が等しいければよいのです。

特に，固有方程式:Φ_T(λ)＝0　が重根をもたなければ，つまり，相異なる固有値をVの次元と等しいn個持っている Tは対角化可能なことは直ちにわかります。では，定理の証明です。

［証明］　必要性:

［３］　 ステップ １　

ことを示します。

　Tが対角化可能ならば，ある基底変換の行列 (正則行列)，

P＝(p₁,p₂,･･･,p_n) [#] が存在して，P^-1TP ＝ D　
  ［ D: 対角行列で対角成分は，μ₁,μ₂,･･･,μ_n ］

とかけます[#]。この式の左から P をかけると，TP＝PD，これを成分で書くと，(P^-1はP の逆行列)

TP＝(Tp₁,Tp₂,･･･,Tp_n)

PD＝(p1,p2,･･,pn)		μ1	0･････0	0		＝(μ1p1,μ2p2,･･･,μnpn)
		0	μ2 0･･0	0
		0	･････0	μn

赤で示した行列の各列をおのおの比較すれば，

Tp_j＝μ_jp_j　　　(j＝1,2,･･･,n)

これは行列T の固有方程式であり，固有ベクトルがp_j，対応する固有値がμ_j( j＝1，2，･･･，n )であることを示しています。さらに，P が正則である[#]ことから，｜P｜≠0，すなわち，p₁，p₂，･･，p_n が１次独立であることもいえます[#]。したがって，このV上のn個のベクトルは，n次元ベクトル空間V を張ることができます。

(注意:　p₁，p₂，･･，p_n が１次独立でも固有値μ_kがすべて相異なるとは限りません。また，μ_kはλ₁，･･･λ_mのいずれかに相当しています。)

［４］　 ステップ ２　

ここで，n個の１次独立な固有ベクトルp₁，p₂，･･，p_n を固有値が等しいものどおし集め，次のように記号を改めます。

λ₁　:　　p(1)₁，･･･，p(1)_d1　　:　d₁個　(＝固有値λ₁の重複度)
λ₂　:　　p(2)₁，･･･，p(2)_d2　　:　d₂個　(＝固有値λ₂の重複度)

･････････

λ_m　:　　p(m)₁，･･･，p(m)_dm　 :　d_m個　(＝固有値λ_mの重複度)

(もちろん，すべての固有値が異なれば，d₁＝d₂＝･･･＝d_m＝1)
ここでの操作はn個の１次独立な固有ベクトルp_j を並び替えただけなので，ベクトル p(i)_j の全個数はn個 で，

n　＝d₁＋d₂＋･･･＋d_m　　　　　　　　　　･･･････････　　[*]

が成り立ち，基底:

｛p(1)₁,･･･,p(1)_d1,p(2)₁,，･･･,p(2)_d2　,･･･,p(m)₁,･･･,p(m)_dm ｝

で，n次元ベクトル空間 V を張ることができます。また，各固有空間E(λ_k)には少なくとも1次独立なd_k個のベクトル｛p(k)₁,･･･,p(k)_dk｝を含んでいるので，その次元について，

dimE(λ_k)≧d_k

でなければいけないことがわかります。ところが，前ページで示したように，dimE(λ_k)≦d_k なので　[#]，結局，

dimE(λk)＝dk

が成り立ちます。(必要性の証明終わり)

なお，[*] は次のように書き換えた方が便利。

dimV ＝ dimE(λ1)＋dimE(λ2)＋･･･＋dimE(λm)  ･･･　[**]

十分性：

［６］　十分性の証明です。さっそく上で定義した用語を使いましょう。[**]が成り立つということは，すなわち，

Tの固有空間:E(λ₁)，E(λ₂)，･･･，E(λ_m) によって，V が直和分解されていることです。このとき，各固有空間の基底を

E(λ₁)の基底:Σ₁＝｛ｅ₁,･･･,ｅ_s｝
E(λ₂)の基底:Σ₂＝｛ｅ_s+1,･･･,ｅ_s+t｝
　　　　････････
E(λ_m)の基底:Σ_m＝｛ｅ_v+1,･･･,ｅ_v+u｝　　

ただし，s＋t＋･･･＋u＝n であり，合計 n個のベクトル，

｛ｅ₁,･･･,ｅ_s ,ｅ_s+1,･･･,ｅ_s+t,･･･,ｅ_v+1,･･･,ｅ_v+u｝

は互いに１次独立であり，ベクトル空間V の基底になっているとします。

［８］　すると，このn個の基底ベクトル(縦ベクトル)をこの順に並べて作った行列，

Q ≡(ｅ₁,･･･,ｅ_s ,ｅ_s+1,･･･,ｅ_s+t,･･･,ｅ_v+1,･･･,ｅ_v+u )　　

は正則です。このとき，TQを計算すると，

TQ　＝(Tｅ₁,･･･,Tｅ_s,Tｅ_s+1,･･･,Tｅ_s+t,･･･,Tｅ_v+1,･･･,Tｅ_v+u )
　　＝(λ₁ｅ₁,･･･,λ₁ｅ_s,λ₂ｅ_s+1,･･･,λ₂ｅ_s+t,･･･,λ_mｅ_v+1,･･･,λ_mｅ_v+u )

＝(ｅ1,･･･,ｅs ,ｅs+1,･･･,ｅs+t,･･･,ｅv+1,･･･,ｅv+u )

λ1 O : λ1 λ2 O : λ2 : λm

＝ QD

となります。　ここで，Dは対角成分として，

E(λ₁)の固有値λ₁が　s個
E(λ₂)の固有値λ₂が　t個
　　　　････････
E(λ_m)の固有値λ_mが　u個

が左上から順に並んだ対角行列です。Q は正則行列なので，Q^-1を上式の左からかけて，

Q^-1TQ＝D

となり，これはQによりTが対角行列Dに変換できることを示しています。 つまり，[**]であるならば，T が対角化可能であること [十分性］ が示されました。

(証明終)

ここまでの議論はざっくりとした一般論，概念的な話で，次ページから具体的なテクニックも含んだ内容に切り込んでいきます。

↓　下図で全体像を掴んでいた方がモヤモヤしなくて済むかもしれません。

［目次へ］

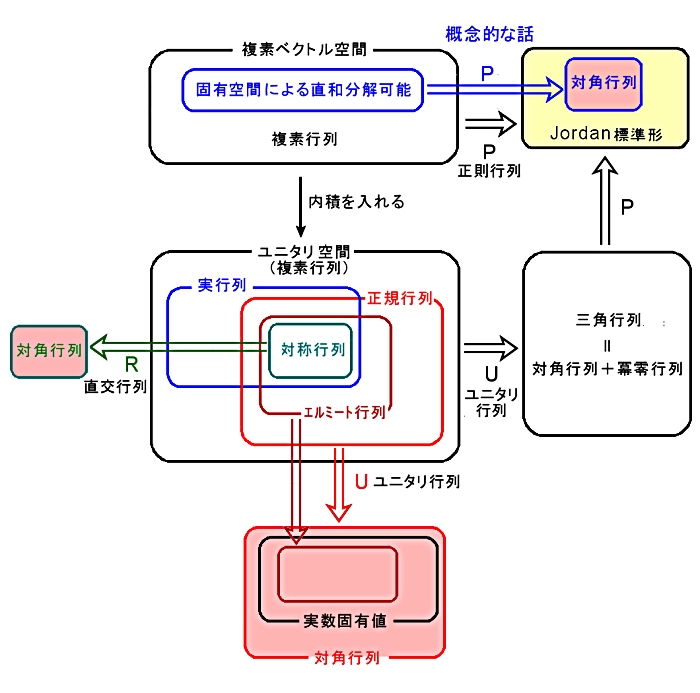
補足:

べクトル空間 V は固有空間によって直和分解される。 　　(次元については何も言えない･･。)

証明:

j ＝ 1,2,･･･,m に対して，

Tx_j＝λ_jx_j

なので，(h1)に T を左からかけて，

Tx₁＋Tx₂＋････＋Tx_m　
                        ＝λ₁x₁＋λ₂x₂＋････＋λ_mTx_m ＝0　

(h1)に λ₁を左からかけて，

λ₁x₁＋λ₁x₂＋････＋λ₁Tx_m ＝0　

辺々引くと，

0 ＋(λ₂−λ₁)x₂＋(λ₃−λ₁)x₃＋･･･＋(λ_m−λ₁)x_m ＝0　 　･･　(h2)

再び，T を左からかけて，

(λ₂−λ₁)Tx₂＋(λ₃−λ₁)Tx₃＋･･･＋(λ_m−λ₁)Tx_m 
　　　＝(λ₂−λ₁)λ₂x₂＋(λ₃−λ₁)λ₃x₃＋････＋(λ_m−λ₁)λ_mx_m ＝ 0

(h2)からλ₂を左からかけて，

＝(λ₂−λ₁)λ₂x₂＋(λ₃−λ₁)λ₂x₃＋･･･＋(λ_m−λ₁)λ₂x_m ＝ 0

辺々引いて，

　　0 ＋(λ₃−λ₁)(λ₃−λ₂)x₃＋･･･＋(λ_m−λ₁)(λ_m−λ₂)x_m ＝0　 ････　(h3)

これを繰り返すと，

(λ_m−λ₁)(λ_m−λ₂)･･･(λ_m−λ_m-1)x_m ＝0　

ここで，係数は0でないので，x_m ＝0　 であることがわかりました。　さらに，

x₁＋x₂＋･･･＋x_m-1＝0　  

について同じように繰り返せば，x_m-1＝0　が証明でき，これを繰り返せば，

x_m＝0，･･･，x₂＝0，x₁＝0

であることが証明できます。