|
t121 1次元イジングモデル |
| f-densHi.com 更新日: |
| サイト検索 |
| 目次へ |
1次元イジングモデルは相転移現象は示さないが,転送行列を用いて厳密解を導くことが可能であったり,厳密に繰り込み変換を行うことができるなど,相転移の研究における基本的な技法と概念を計算機を駆使することなく示すことができるという有用性を備えています。ここでは,これらのテクニックについて簡単に紹介します。
1.転送行列を用いた解法
[1] 1次元イジングモデルのハミルトニアンを
| H=-J |
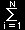 |
σiσi+1−H |
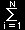 |
σi |
とします。σi はスピン変数で+1,または-1の値をとります。第1項は最近接スピンどおし間だけに存在する交換相互作用で大きさを係数Jで表します。第2項は各スピンと外部磁場Hとの相互作用を表していますが,スピン1つ当たりの磁気モーメントはここでは簡単のため1とします。また,周期境界条件,σN+1=σ1を適用します。
すると,この系の分配関数は,
| = |
|
exp |
 |
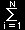 |
 |
Kσiσi+1+h |
σi+σi+1 |
  |
|
| 2 |
ただし,
で与えられます。
[2] 具体的に計算を進めるために次のようなスピン基底:{|+>,|−>} [#] に基づくブラケット記法を導入し,
| |σi>= |
 |
| |σi=+1>=|+>= |
 |
1 |
 |
[σi=+1のとき] |
| 0 |
|
|
| |σi=-1>=|−>= |
 |
0 |
 |
[σi=-1のとき] |
| 1 |
|
| <σi|= |
 |
<σi=+1|= <+|=( 1 0 ) [σi=+1のとき] |
|
| <σi=-1|=<−|= ( 0 1 ) [σi=-1のとき] |
この基底の下で,転送行列 T を成分が,
| <σi|T|σi+1>=exp |
 |
Kσiσi+1+h |
σi+σi+1 |
 |
|
| 2 |
|
であるように定義します。すなわち,
| T = |
 |
<σi=+1|exp(βH)|σi+1=+1> <σi=+1|exp(βH)|σi+1=-1> |
 |
| <σi=-1|exp(βH)|σi+1=+1> <σi=-1|exp(βH)|σi+1=-1> |
ここで,ブラは i 番目のスピン,ケットは i+1 番目のスピンの状態というように一つずらして対応させていることに注意してください。
これを計算すれば,
| T= |
 |
exp(K+h) |
exp(−K) |
 |
| exp(−K) |
exp(K−h) |
|
が得られます。
[3] このTを用いると分配関数Zは,
| Z= |
|
exp |
 |
Kσ1σ2+h |
σ1+σ2 |
 |
・exp |
 |
Kσ2σ3+h |
σ2+σ3 |
 |
・・・ |
|
|
| 2 |
2 |
| = |
|
<σ1|T|σ2><σ2|T|σ3>・・・・・<σN|T|σN+1> |
と書くことができます。さらに,ブラケットの完備性,
である[#]ことを利用して,計算を進めていくと,
=<+|TN|+> + <−|TN|−>
これは,行列 TN のトレース(対角和)に他なりません。
[4] トレースは基底の選び方によらない[#]ので,Tが対角行列となるように基底変換行列Uを用いて,Tの固有値,λ+,λ-が対角成分に並らぶように,
| U-1TU= |
 |
λ+ |
0 |
 |
| 0 |
λ- |
|
⇒ |
| U-1TNU= |
 |
λ+N |
0 |
 |
| 0 |
λ-N |
|
と変換すれば,分配関数はこのトレースから,
と表すことができます。また,この2つの固有値は固有多項式,
|T−λE|=0
を解けば,
| λ±=eKcosh(h) ± |
|
|
 |
e2Ksinh2(h)+e-2K |
|
と得られます(複合同順とする)。(これは2次方程式を解くだけ。)
さらに,λ+>λ- より,Nが大きいときは,Z=λ+N と近似できるので,結局,
| Z= |
 |
eKcosh(h)+ |
|
|
 |
e2Ksinh2(h)+e-2K |
|
 |
N |
・・・[*] |
|
が得られます。
[5] 分配関数が分かれば,様々な熱力学量は以下のような計算から導出することができます。
自由エネルギー
自由エネルギーは,F=−kT log Z より,
| F =−NkT log |
 |
eKcosh(h)+ |
|
|
 |
e2Ksinh2(h)+e-2K |
|
 |
| =−NJ−NkT log |
 |
cosh(h)+ |
|
|
 |
sinh2(h)+e-4βJ |
|
 |
|
磁場が0(h=0)のときの自由エネルギー
| F =−NkT log [ eK+ |
|
|
] |
 |
e-2K |
|
=−NkT log[2cosh K]
=−NkT log[2cosh βJ]
磁場が0(h=0)のときの内部エネルギー [#]
| <E>=− |
∂log Z |
= |
∂ |
Nlog[2cosh βJ ] |
|
|
| ∂β |
∂β |
=−NJ tanhβJ
=−NJ tanh[J/kT]
磁場が0(h=0)のときの比熱
| C=− |
∂E |
=Nk |
 |
J |
 |
2 |
sesh2[ J/kT] |
|
|
| ∂T |
kT |
これより,比熱は温度の関数として,T>0 では異常性を示さない(少なくとも1階微分可能な連続関数である)ことが分かります。 事実,これは単純な2準位系の比熱[#}と関数形が同じになっています。
|
参考: (単純な)2準位系の比熱
| Cv=Nk |
 |
ε |
 |
2 |
sech2 |
ε |
[等積比熱] |
|
|
|
| kT |
|
kT |
|
[6] イジングモデルが適用される代表的な描像として,磁化を考えます。
磁化率
まず,分配関数の定義,
に戻り,この対数をとって,hで微分すれば,
| ∂log Z |
= |
1 |
・ |
∂Z |
= |
|
|
(σ1+σ2+・・・+σN)exp |
 |
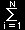 |
 |
Kσiσi+1+hσi |
  |
|
|
|
|
|
Z |
|
|
|
|
| ∂h |
Z |
∂h |
=N<σi> =M [(巨視的な)磁化]
したがって,磁化は上式に[*]を代入して,
| M= |
∂ |
| N log |
 |
eKcosh(h)+ |
|
|
 |
e2Ksinh2(h)+e-2K |
|
 |
|
|
| ∂h |
| = |
N |
・ |
 |
| eKsinh(h)+ |
e2Ksinh(h)・cosh(h) |
|
|
|
 |
e2Ksinh2(h)+e-2K |
|
|
 |
|
| eKcosh(h)+ |
|
|
 |
e2Ksinh2(h)+e-2K |
|
|
| = |
N |
・ |
| eKsinh(h) |
{ |
|
|
|
 |
e2Ksinh2(h)+e-2K |
+eKcosh(h) |
|
} |
|
|
|
 |
e2Ksinh2(h)+e-2K |
|
|
|
| eKcosh(h)+ |
|
|
 |
e2Ksinh2(h)+e-2K |
|
|
| = |
N sinh(h) |
|
|
|
|
 |
sinh2(h)+e-4K |
|
これより,このモデルの帯磁率は,
| χ= |
 |
∂M |
 |
H=0 |
|
| ∂H |
| = |
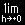 |
 |
N cos(h) |
− |
N sinh2(h)・cosh(h) |
 |
∂h |
|
|
|
|
|
|
 |
sinh2(h)+e-4K |
|
(sinh2(h)+e-4K)3/2 |
∂H |
=Ne2Kβ
| = |
N |
exp |
 |
2J |
 |
|
|
| kT |
kT |
と定義できます。特に高温においては,
となり,キュリーの法則(キュリー温度Tc=0K)が確認できます。
一方,絶対零度において,磁化率は+∞に発散することが分かります。つまり,交換相互作用をもつ1次元磁性体は絶対零度の極限において強磁性体へ転移すると考えることもできます。
結論として,1Dイジングモデルから導かれる強磁性-常磁性の転移温度は絶対零度であり,この系は有限温度T>0においていつも常磁性領域に相当する高温相にあるといえます。
[目次へ]
SUSTAINABLE TOKIWADAIGAK SINCE 2002
補
「トレース(対角和)は基底によらない。」
基底変換(相似変換行列をPとして),B=P-1AP であるとき,
trB=tr[P-1AP ]=tr[P-1(AP)]
=tr[(AP)P-1] ← 一般的にtr[PQ]=tr[QP]
=tr[(A(PP-1)]
=tr[(AE]=trA
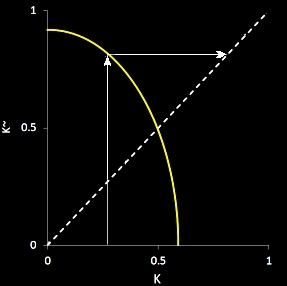
繰り込み群とならないような変換を例示しておけば,例えば,縦長の楕円を表すような関数だと繰り込み変換とはなりません。