| 8-1 ルジャンドル変換 | ||
| f-denshi.com [目次] 最終更新日: 21/08/30 図を付けました | ||
| サイト検索 | ||
全微分可能な2変数関数のもっとも重要な応用の一つを紹介します。物理や化学(解析力学,熱力学)において,そこで使われる未知数(変数)の数が独立な未知数より多いことがあります。そのような場合,あるいくつかの未知数の値が定まると残りの未知数の値も自動的に決まってしまいます。この未知数を相互に関係づける解析的な表現の一つがルジャンドル変換です。この章では熱力学諸関数間の変換で使われる4変数の場合を例にとり説明しましょう。
[1] 関数や方程式を扱うときしばしば,変数の置き換え(変数変換)が行われます。例えば,2つの独立変数に関する関数,
f(x,y) = 2x+2y+3xy
は,x+y =α,xy = β と置き換えることで,
f(x,y) ⇒ g0(α,β) = 2α+ 3β
となります。または部分的な置き換えによって,
f(x,y) ⇒ g1(α,y) = 2α+ 3(α−y)y
f(x,y) ⇒ g2(x,α) = 2α+ 3x (α−x)
f(x,y) ⇒ g3(x,β) = 2(x+β/x)+3β
f(x,y) ⇒ g4(β,y) = 2(β/y+y)+3β
などとも表すことができます。もちろん,これら6つの式の意味する内容はおなじであり,4つの変数,x,y,α,β が現れますが,この問題における独立変数は2つだけです。
[2] さて,以上の前置きを念頭に今度は全微分を利用した同様な変数の置き換えを行ってみましょう。
(1) 変数 x,y を独立変数とする全微分可能な関数をφ(x,y) とします。全微分は
dφ = ∂φ dx + ∂φ dy ∂x y ∂y x
ここで,
u = ∂φ , v = ∂φ ∂x y ∂y x
と変数を導入して置き換えれば,
dφ = udx + vdy
と書けます。そして,この式の u や v を独立変数とみなす関係式を見出そうというのがこれからの作業です。
(2) まず,φ(x,y) において変数変換 ( x → u ) を行いたいときは,
ψ = φ−xu
と関数ψを定義すれば,
dψ= dφ−d(xu)
= (udx+vdy)−(xdu+udx)
= −xdu + vdy
と,ψが u,y の関数として表せていることがわかります。これを u,y を独立変数とするψ(u,y)の全微分,
dψ= ∂ψ du + ∂ψ dy ∂u y ∂y u
と比較すれば,下のような関係が成り立っていなければなりません。
- x = ∂ψ , v = ∂ψ ∂u y ∂y u
(3) 次に,φ(x,y) の変数のうち (y → v) と換えたいときは,
λ = φ−yv
dλ = dφ−d(yv)
= (udx+vdy)−(ydv+vdy)
= udx − ydv
とすればよいことがわかります。これを全微分,
dλ= ∂λ dx+ ∂λ dv ∂x v ∂v x
と比較して,
u = ∂λ ,−y = ∂λ ∂x v ∂v x
(4) 同じような計算の繰り返しですが,ψ(u,y) の変数を (y → v) と換えるために,μ=ψ− yv と置くと,
dμ=dψ−d(yv)
=(−xdu+vdy)−(ydv+vdy)
=−xdu − ydv
これを全微分,
dμ = ∂μ du + ∂μ dv ∂u v ∂v u
と比較して,
−x = ∂μ , −y = ∂μ ∂u v ∂v u
が得られます。 以上が必要な関係式のすべてです。
[3]以下,蛇足ですが,
(4)' λ(x,v)の変数を(x→u)と換えるために μ'=λ−xu と置くこともできますが,
dμ'= dλ−d(xu)
= (udx−ydv)−(xdu+udx)
= −ydv−xdu
つまり,μ=μ'とすることができます。( つまり,上の置き換えから新しいことは何もでてこない! )
(4)'' また,φ(x,y)より一度に2つの変数を(x→u,y→v)と換えることもでき,
μ''= φ−xu−yv
と置いて,
dμ''= dφ−d(xu)−d(yv)
= (udx+vdy)−(xdu+udx)−(ydv+vdy)
= −ydv−xdu
つまり,μ''= μですが,これまでの計算をよく見ると,
μ''= φ−xu−yv = ψ−yv = λ−xu
などとなり,μ'' もさらに新しい関数を定義するものではありません。
[4] 以上,計算結果を一覧表にすると,下のように整理できます。
| φ(x,y) | ψ(u,y) | λ(x,v) | μ(u,v) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (φ=ψ+xu ) | ψ=φ−xu | λ=φ−yv | μ=ψ−yv | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (φ=λ+yv) | (ψ=μ+yv) | (λ=μ+xu) | μ=λ−xu | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (φ=μ+xu+yv) | (μ=φ−xu−yv) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (1) dφ=udx+vdy | (2) dψ=−xdu+vdy | (3) dλ=udx−ydv | (4) dμ=−xdu−ydv | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
例 下に凸な2変数関数 φ(x,y)=x2+y2 をルジャンドル変換していくと,上表に対応する下表を得ることができます。
| φ(x,y) = x2+y2 | ψ(u,y) = −u2/4+y2 | λ(x,v) =x2−v2/4 | μ(u,v)=−(u2+v2)/4 |
| (φ=ψ+xu ) | ψ=φ−xu | λ=φ−yv | μ=ψ−yv |
| (φ=λ+yv) | (ψ=μ+yv) | (λ=μ+xu) | μ=λ−xu |
| (1) dφ=udx+vdy | (2) dψ=−xdu+vdy | (3) dλ=udx−ydv | (4) dμ=−xdu−ydv |
| u=2x : v=2y | -x=−u/2 : v=2y | u=2x : -y=−v/2 | -x=−u/2 : -y=−v/2 |
φ(x,y)=x2+y2 ⇒ ψ(u,y) への計算方法を示しておくと,
u= ∂φ =2x ∂x y
ψ(u,y)=φ(x,y)−xu = (u/2)2+y2−(u/2)u
=−u2/4+y2
残りも同様です。
[6] 以上得られた4つの関数,φ(x,y),ψ(u,y),λ(x,v),μ(u,v) を図示すると下記のとおりです。
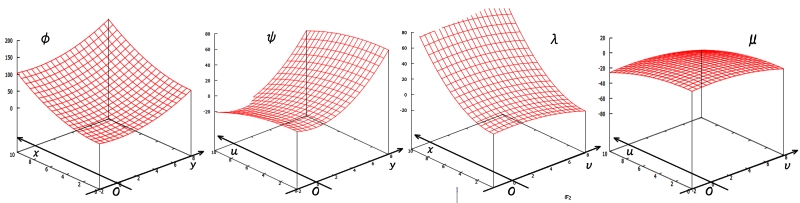
φは下に凸な関数,μは上に凸な関数です。また,ψ,λは各 座標成分=一定 の断面が成分ごとに上下反対方向に凸な関数となっており,全体として (0,0) に鞍点をもつ形状をしています。
[1] 熱力学への応用です。上の一覧表 [#] で,記号の置き換え,
φ → H [エンタルピー], x → S [エントロピー] ψ → G [ギブスの自由エネルギー] y → P [圧力] λ → U [内部エネルギー] u → T [温度] μ → F [ヘルムホルツの自由エネルギー] v → V [体積]
を行うと熱力学諸関数の相互変換の式がそっくり GET できるのです。
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
熱力学の教科書では結構,見通しの悪い計算と説明をだらだらとすることになるのですが,数学的なエッセンスを抽出してしまえば,意外とあっさりとしていること,理解していただけましたか? もちろん,これだけでは熱力学を理解したことにはなりませんが,・・・・
[1] 前半1.は私が学生時代に自己流にルジャンドル変換を解釈したもので,教科書にそのような説明を見かけることはないと思います。
そこで,正統なルジャンドル変換の話も付け加えたいと思います。
ルジャンドル変換は,
「凸関数 y=f(x) をその傾き p と y切片 g(p) で表す。」
ための変換操作と言うことができます。
変数変換というよりは,関数 f(x) から付随する別の関数 g(p) を作り出すという意味合いです。より一般化したものは,ルジャンドル・フェンシェル変換と呼ばれ,ウィキペディアにも簡単な説明があります。 ⇒ 凸共役性 (初学者が読むには少し難しいかも。)
関数形 g は凸関数 f が与えられると,一意的に定まります。凸関数でなくても形式的にルジャンドル変換はできますが,変換前後の関数に1対1対応がないので,そのまま全体には「共役性」が存在しません。
ルジャンドル変換が熱力学関数で有用なのはそれら関数が凸関数だからです [#]。
同じ定義には,sup,inf を使って行うものがあります。
g(p)=sup{xp−f(x)}
この変換は,2変数関数の場合は,各変数についてそれ素ぞれ別々に考えます。
[2] 次は解析力学における例です。ラグランジアンと(符号を反転した)ハミルトニアンの関係:
−H(q,p)=L(q,q')−q'p
| が ルジャンドル変換(q'→p) になっています。 ただし,q'= | dq |
| dt |
先の4変数のルジャンドル変換のうちで今必要なのは,第1列と3列だけです。抜き出すと,
φ(x,y) λ(x,v) φ=λ+yv λ=φ−yv, dφ=udx+vdy dλ=udx−ydv
u= ∂φ :v= ∂φ ∂x y ∂y x
u= ∂λ :−y= ∂λ ∂x v ∂v x
となります。上の表で,
x → q , y → q', v → p , φ → L , λ → −H
と置き換えると,
L(q,q') -H(q,p) L=-H+q'p −H=L−q'p dL=udq+pdq' −dH=udq−q'dp
u = ∂L : p = ∂L ∂q q' ∂q' q
u = ∂-H :-q'= ∂-H ∂q P ∂p q
がハミルトニアンとラグラジアンをつなぐルジャンドル変換のかかわる部分です。
[3] 赤枠内の2式と,オイラー・ラグランジュ(E - L)の方程式[#] ,(←この方程式は解析力学を参照してください。)
∂L = d ∂L ∂q dt ∂q'
から,
u = ∂L =
(E-L方程式)d ∂L = dp ∂q dt ∂q' dt
これと黄枠の2式を使えば,ハミルトンの正準方程式
|
が得られます。
以上は解析力学のところで詳細に説明しています。