| Appendix 3 熱平衡状態の安定性 | ||
| f-denshi.com 更新日: 09/04/26 | ||
| サイト検索 | ||
熱平衡状態の安定性というテーマは,どちらかと言えば平衡熱力学の中ではあまり重要ではありません。正確に言えば,このテーマをしっかり取り扱おうとすると,非平衡熱力学(非平衡統計力学)の分野に入っていかないといけなくなり,平衡熱力学の範囲で何かをしゃべることとなると,実につまらない結論ばかりとなる。
熱力学安定性と関連した話題としてルシャトリエ・ブラウンの法則 ⇒ [#] や不均一系(2相共存平衡)の安定性 ⇒ [#] などがありますが,それらは潜熱を考慮する必要があり,ここでの議論の対象ではありません。)
[1] 熱力学関数の極値として,様々な熱平衡条件が表現されることがわかりました[#]が,これを具体的に解くためには多変数関数の条件付極値問題に関する数学的な知識が必要となります。例えば,ときわ台学:「実数解析入門」,「変分原理と解析力学」中の次のような知識が必要となります。
(1) 多変数関数の極値問題 [#]
(2) 条件付極値問題 [#]
(3) 対称行列(〜ヘッセ行列) の固有値問題 [#]
これらをすべて復習するのが面倒だという方は次の囲みの中だけでも読んでから先へ進んでください。
|
考え方: δf≡f(a+δx)−f(a)<0 であり,逆も成り立つことがわかります。ここで,δx の項を第一変分,(δx)2の項を第二変分と呼びましょう。すると極大値である条件は, 「第一変分が 0,かつ第二変分が負」 という言い方ができます。 この流儀を多変数の場合に拡張した数学的な議論が(1)〜(3)ということです。 |
 [1] まず,熱だけをやり取りし,粒子は交換しない2つの相,相(α)と相βからなる容積一定の断熱容器に閉じ込められた孤立系を考えます。イメージしては右図のようにお互いに交じり合わないヘキサンと水が密閉容器のなかに閉じ込められている状況を考えるとよいでしょう。もっとも簡単な不均一系です。直感から相αと相βの温度が等しいことが平衡条件だとわかりますが,一般的な熱力学平衡条件からこれを導出してみましょう。この系の拘束条件は各相の体積変化が無視できる場合,
[1] まず,熱だけをやり取りし,粒子は交換しない2つの相,相(α)と相βからなる容積一定の断熱容器に閉じ込められた孤立系を考えます。イメージしては右図のようにお互いに交じり合わないヘキサンと水が密閉容器のなかに閉じ込められている状況を考えるとよいでしょう。もっとも簡単な不均一系です。直感から相αと相βの温度が等しいことが平衡条件だとわかりますが,一般的な熱力学平衡条件からこれを導出してみましょう。この系の拘束条件は各相の体積変化が無視できる場合,
δV(α)=δV(β)=0, ← V(α),V(β)=一定
δU(α)+δU(β)=0 ← U(α)+U(β) =一定
となります。この条件下で全エントロピー:
S=S(α)(U(α),V(α))+S(β)(U(β),V(β))
↑ 熱力学第1法則から,UはSとVとで決まる[#]が,その関係をSについて解いた式。
の極値条件,δS=0 (必要条件)は,δV(α)=δV(β)=0 なので,← 孤立系の熱力学平衡条件でした[#]。
δS= ∂S δU(α)+ ∂S δU(β)= 0 ∂U(α) V(α) ∂U(β) V(β)
さらに,前章の公式(9)’[#]を用い,δU(β)=−δU(α) を代入すると,
δS= 1 − 1 δU(α)= 0 T(α) T(β)
と変形できます。任意のδU(α)に対してこの等式が成立するためには,T(α)=T(β) でなければいけません。これがこの系が熱力学平衡にある必要条件です。
[2] 次に十分条件 δ2S<0 (エントロピーが極大) について考えて見ましょう。ここでも,δV(α)=δV(β)=0 に注意して,
δ2S=δ(δS)
| =δ | δU(α) | + | δU(β) | ||
| T(α) | T(β) |
| = | 1 | δ(δU(α))+ | 1 | δ(δU(β))+ | ∂T(α) -1 | (δU(α))2+ | ∂T(β) -1 | (δU(β))2 |
| T(α) | T(β) | ∂U(α) | ∂U(β) |
↓ δ(δU(α) +δU(β) )=0, T(α) =T(β) ≡Tより第1項+2項=0
= − 1 ・ ∂T (δU(α) )2− 1 ・ ∂T (δU(β) )2 T2 ∂U(α) T2 ∂U(β)
= − 1 ∂T + ∂T (δU(α) )2 T2 ∂U(α) ∂U(β)
↓ 各相の体積が一定のもとで考えているので,等積比熱[#]に直すことができて,
= − 1 1 + 1 (δU(α) )2 < 0 T2 Cv(α) Cv(β)
これが任意の(δU(α) )2について成り立つためには,CV(α),CV(β)が常に正でなければいけません。一般的に物質の等積比熱は正であるということができます。ここでの結論と CP > CV [#] より,
CP> CV > 0 [物質の比熱は正である] |
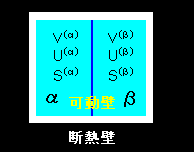 [1] 今度は系が2種類の気体,たとえば,炭酸ガス(α相),ヘリウムガス(β相)からなり,それらが混合しないように隔壁で仕切られているような場合を考えます。ただし,隔壁は熱を自由に通過させ,左右両相の圧力に応じてその位置が自由に動く可動壁ということにしておきます(右図参照)。また,これら全体は断熱壁で覆われている,すなわち,孤立系とします。その場合,体積に関係する拘束条件は,先ほどのヘキサン-水系で用いた
δV(α)=δV(β)=0 から,
[1] 今度は系が2種類の気体,たとえば,炭酸ガス(α相),ヘリウムガス(β相)からなり,それらが混合しないように隔壁で仕切られているような場合を考えます。ただし,隔壁は熱を自由に通過させ,左右両相の圧力に応じてその位置が自由に動く可動壁ということにしておきます(右図参照)。また,これら全体は断熱壁で覆われている,すなわち,孤立系とします。その場合,体積に関係する拘束条件は,先ほどのヘキサン-水系で用いた
δV(α)=δV(β)=0 から,
δV(α)+δV(β)=0
へと変更されます。また,全エントロピー,
S=S(α)(U(α),V(α))+S(β)(U(β),V(β))
の極値の必要条件,δS=0 は,
| δS= | ∂S | δU(α)+ | ∂S | δU(β)+ | ∂S | δV(α)+ | ∂S | δV(β)=0 | ||||||||||||
| ∂U(α) | V(α) | ∂U(β) | V(β) | ∂V(α) | U(α) | ∂V(β) | U(β) |
となります。このとき,内部エネルギーに関する変分の係数を0とするところからは,具体例(1)とまったく同じように,T(α)=T(β)が導かれます。一方,内部エネルギーとは独立に仮想変化させる体積部分の変分は, (TdS−PdV =dU に注意して)
↓ TdS−PdV =dU
δS'= ∂S δV(α)+ ∂S δV(β) ∂V(α) U(α) ∂V(β) U(β)
= P(α) − P(β) δV(α)= 0 T(α) T(β)
となり,これが新たな必要条件として追加されます。結局,
T(α)=T(β) かつ,P(α)=P(β) → δT(α)=δT(β)=0,δP(α)=δP(β)=0
が熱力学平衡条件となります。つまり,温度だけではなく,2つの相の圧力も等しくなくてはいけません。
[2] 次に,十分条件を求めるために第2変分 δ2S < 0 について考えましょう。早速,計算を始めると,
| δ2S=δ | δU(α) | + | δU(β) | + | P(α) | δV(α)+ | P(β) | δV(β) | |||||
| T(α) | T(β) | T(α) | T(β) | ||||||||||
| =− | δU(α)δT(α) | − | δU(β)δT(β) | + | δP(α) | δV(α)+ | δP(β) | δV(β)− | P(α) | δT(α)δV(α)− | P(β) | δT(β)δV(β) | |
| T(α)2 | T(β)2 | T(α) | T(β) | (T(α))2 | (T(β))2 |
| = | − | δU(α)+P(α)δV(α) | δT(α)− | δU(β)+P(β)δV(β) | δT(β)+ | δP(α) | δV(α)+ | δP(β) | δV(β) |
| T(α)2 | T(β)2 | T(α) | T(β) |
↓ δU(α)+P(α)δV(α)=T(α)δS(α) などより
| =− | δS(α) | δT(α)+ | δP(α) | δV(α)− | δS(β) | δT(β)+ | δP(β) | δV(β) | ・・・[*] |
| T(α) | T(α) | T(β) | T(β) |
一方で,変分量δS(α)は,公式(17),マックスェルの関係式(15)より,
δS(α)= ∂S(α) δT(α)+ ∂S(α) δV(α) ∂T(α) ∂V(α)
= Cv(α) δT(α)+ ∂P(α) δV(α) T(α) ∂T(α)
また,
δP(α)= ∂P(α) δT(α)+ ∂P(α) δV(α) ∂T(α) ∂V(α)
これらを[*]のα相の関わる第1項+第2項に代入すれば,(訂正09/10/09↓)
| − | δS(α) | δT(α)+ | δP(α) | δV(α)=− | Cv(α) | (δT(α))2− | 1 | ∂P(α) | δV(α)δT(α)+ | 1 | ∂P(α) | δT(α)δV(α)+ | 1 | ・ | ∂P(α) | (δV(α))2 | ||||
| T(α) | T(α) | T(α)2 | T(α) | ∂T(α) | T(α) | ∂T(α) | T(α) | ∂V(α) | ||||||||||||
β相の関わる第3項,第4項についても同様です。したがって,[*]は,
| δ2S=− | Cv(α) | (δT(α))2+ | 1 | ・ | ∂P(α) | (δV(α))2− | Cv(β) | (δT(β))2+ | 1 | ・ | ∂P(β) | (δV(β))2 | |||
| T(α)2 | T(α) | ∂V(α) | T(β)2 | T(β) | ∂V(β) | ||||||||||
=− Cv(α) + Cv(β) (δT(α))2+ 1 ・ ∂P(α) + 1 ・ ∂P(β) (δV(α))2 T(α)2 T(β)2 T(α) ∂V(α) T(β) ∂V(β)
これが任意のδT(α),δV(α) について負であるためには,T(α)=T(β)であることに注意して
Cv(α)+Cv(β)>0, ∂P(α) + ∂P(β) < 0 ∂V(α) ∂V(β)
となります。特に左右の気体が同一種類であるときは,
Cv>0, ∂P < 0 ∂V T
として構いません。またこの条件は等温圧縮率[#],κ>0 と言い直しておいた方がいいでしょう。この結果はファンデルワールス気体が熱力学的に安定な範囲を限定するために使いました[#]。
[1] 熱力学安定性を議論することで,ヘルムホルツ自由エネルギー,ギブス自由エネルギーの温度,圧力,体積依存性の概略を知ることができます。各座標の断面のようすをまとめると,
(1) G,H ともに温度に関して,上に凸である減少関数でなければならない。
(2) Gは圧力に関して,上に凸である増加関数でなければならない。
(3) Fは体積に関して,下に凸である減少関数でなければならない。
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
関数の特徴を決めている各方程式・不等式の導出は,「8.熱力学関数」 [#] をみてください。
「7.熱平衡の条件」で述べたように,自由エネルギーは,状態が変化する方向性を示唆するポテンシャル(可能性)の役割をもつことを考えると,上図の物理的な意味を理解を得ることができます。
[目次へ]
SUSTAINABLE TOKIWADAIGAK SINCE 2002
| κT = − | 1 | ∂V | 定温圧縮率 | |||
| V | ∂P | T |
| κS = − | 1 | ∂V | 断熱圧縮率 | |||
| V | ∂P | S |
κT ≧κS>0
| Cp | = | κT |
| Cv | κS |
ここでは,T,P の関数: G(T,P) が2階連続微分可能で,次のようにテーラー展開されることを前提として,話を進めましょう。
G(T+δT,P+δP) = G(T,P)
+ 1 δT ∂G(T,P) +δP ∂G(T,P) 1! ∂T ∂P
+ 1 (δT)2 ∂2G(T,P) +2(δT)(δP) ∂2G(T,P) +(δP)2 ∂2G(T,P) +高次の項 2! ∂T2 ∂T∂P ∂P2
安定であるというのは極小値をとる十分条件として2次の変分量が正であること。