ルシャトリエ・ブラウンの原理
|
13 質量作用の法則と ルシャトリエ・ブラウンの原理 |
|
| f-denshi.com ［目次へ］ 更新日： 21/09/04 | ||
| サイト検索 | ||
１． 質量作用の法則
［１］ 多成分系を構成する物質(分子) に化学反応が起こると，系の各成分は化学反応に伴う質量の増減が生じます。このとき，消滅する化学種の分子数と生成する化学種の分子数との関係は簡単な整数比で表すことができますが，これを化学量論比 (stoichiometric proportion) と呼びます。例えば，水素ガスと窒素ガスが反応してアンモニアガスが生成する化学反応式は気体状態を (g) として，次のように書かれます。
3H2 (g) + N2 (g)
⇔ 2NH3 (g) ［アンモニアの生成反応］ [反応系] [生成系]
この化学反応は，条件に応じて左右どちら向きに対しても速やかに進むことができる可逆反応です。右方向へ進む化学反応を正反応と呼び，系における水素，窒素の質量(分子数) が減少し，アンモニアの質量が増加します。その際，化学種の増減のモル比は 3 ： 1 ： 2 となります。逆の左方向へ向かう逆反応のときは正反対の質量の増減が起こります。
いま，水素，窒素，アンモニアをそれぞれ，100 モルずつ容器に投入し，温度500 ℃，圧力500atm という条件に固定したとしましょう。すると，時間経過とともに化学反応が進行し，組成が変化していきますが，最終的には左右両方向へ向かう反応が見かけ上つり合い，系の組成はある一定値のまま変化しなくなります。この状態を化学平衡状態といいます。この化学平衡に到達する過程は可逆な化学反応の下で実現しますが，熱力学的には不可逆過程です。
このときの最終状態は熱平衡状態でもあり，系の組成は熱力学的な知見，すなわち，「系のギブス自由エネルギーが極小値をとる」という条件に基づいて予測可能なはずです。その具体的な処方を示すのがこのページの目的です。
［２］ 化学平衡を定量的に記述するために必要な定義をいくつか示します。化学反応式は，
νj Xj ＝ 0 (1)
と表すことにします。ここで，νj はすべて整数で，必要であれば，あらかじめ約分しておきます。アンモニアの生成反応はこの表記法では，
− 3H2 − N2 ＋ 2NH3 ＝ 0 ［アンモニアの生成反応］
と書くことになります。このとき，化学反応 (1) に伴う各成分のモル数の増減には，
δn1：δn2： ･･･ ：δnr ＝ ν1：ν2： ･･･ ：νr
のような関係を見つけることができます。したがって，反応の進行度を示すためのパラメーターδξ を次のように定義することができます。
δnj ＝ νj δξ
(正反応が進行するとき，δξ ＞ 0 としてνj の符号を定める。) (2)
この表記法をアンモニアの生成反応に当てはめると，δξ ＝ 1 のときは，反応によって３モルの水素と１モルの窒素が減少し，２モルのアンモニアが増加することを意味します。一方，δξ＝ -1 のときはこれと全く逆の反応に対応します。
一つ注意しておくことは，ここでの議論は系が任意量，任意組成の混合物であることを念頭に行われており，δξ ＝ 1 は与えられた化学組成の下における化学式量分の化学反応の進行を意味しているだけで，決して正方向への化学反応が (1) 式にしたがい，100 ％完結したという意味ではないことです。
［２］ さて，化学反応によって系の組成がわずかだけ変化したとき，系の全ギブス自由エネルギーがどれほど変化するか計算してみましょう。ここでは，r 個の成分の化学ポテンシャル[#]がすべて各物質の純粋状態の標準化学ポテンシャル [#] とそのモル分率を用いて，
μj(T, P, xj) ＝ μj0 (T, P) + RT log xj (3)
μj0 (T, P)
： 純粋なｊ成分の化学ポテンシャル xj ： ｊ成分のモル分率
と表される ”理想系” と仮定します。すると，温度，圧力が一定の下での化学反応にともなう系の全ギブス自由エネルギー変化[#]は，(2)，(3) を用いて，
δG ＝ μjδnj
＝δξ 
νjμj
＝ δξ νj (μj0 + RT log xj )
これをT, P 一定の下で，δξ で除すと，[*]
ΔrG ≡ ∂G T,P ＝ νj μj0 + RT log xj νj ∂ξ
＝ ΔrG0 + RT log xj νj (4)
が得られます。ここで，
ΔrG0 ≡ νj μj0
を定義しました。
化学反応の進行度ξと全ギブス自由エネルギーG，
および，傾きΔrG との関係。
上図に示すように化学反応の進行度ξ に対して系の全ギブス自由エネルギーG をプロットしたときの，その曲線の傾きがΔrG となります。これは系が十分大きい ( ＞＞ 1mol ) として，ある組成において，dξ ＝ 1 だけ化学反応が進行したときのその組成における系の全ギブス自由エネルギー変化と考えてもよいでしょう。
すると，曲線の傾きが負，ΔrG < 0 であるξ に対応する組成範囲ならば，正反応が自発的に進行し，他方，傾きが正，ΔrG ＞ 0 であるならば，逆反応が自発的に進行すると判断できます。そして，ΔrG ＝ 0 となる組成においてG は極小となり，化学反応は見かけ上停止し，化学平衡に達していると考えることができます。したがって，系が熱平衡にある必要条件は(4) において，ΔrG ＝ 0 として，
ΔrG0 + RT log xjνj ＝ 0 [*]
のように与えられます。これが化学平衡状態にある系の組成に課される必要条件です。
ここで，[*]式の第１項は化学反応に伴う標準自由エネルギー変化 (standard free energy change) と呼ばれ，
ΔrG0 ＝ νj μj0
と定義されています。アンモニア生成反応であれば，
ΔrG0 ＝−3μH20(T, P) −μN20(T, P) + 2μNH30(T, P)
となります。これは正確に化学量論数だけ用意された純粋な水素(３モル)，窒素(１モル) が化学反応式にしたがい，等温，定圧下で純粋な生成物であるアンモニア(２モル) に100 ％変化したとする，言わば，「理想的なアンモニア生成反応」が起きたときのギブス自由エネルギー変化に相当します。
一方，[*] 式の第２項は各成分が混じり合うことによる混合エントロピーの寄与と考えることができます。
この第２項がなければ，ΔrG0 の符号に従って化学反応はいずれかの成分が消費し尽くされるまで正逆どちらかへ一方的に進行するはずです。例えば，ΔrG0 < 0 であるならば，反応は正方向に進むほどギブス自由エネルギーが低いため，反応物質が消費し尽されるまで反応は止まりません。
ところが第２項があるために [*]式を満たす組成において，ギブス自由エネルギーが極小値に到達し，熱平衡(＝化学平衡) 状態に達することができるのです。よって，化学平衡が実現する理由は混合エントロピー効果のおかげだと述べることができます。
ここで，慣用に従い，平衡定数 (equilibrium constant) として，
ΔrG0 (T, P) ＝−RT log K(T, P) ⇔ K(T, P) ≡ exp − ΔrG0 RT
を満足する K(T, P) を定義しましょう。すると，[*] 式は，
log K(T, P) ＝ log xj νj ⇔ K(T, P) ＝ xjνj
と書くことができます。
［３］ 以上の結果について，成分をあらかじめ反応物が前半，生成物が後半に並ぶように，j ≦ k のとき，νj ＜ 0，また，j ＞ k のとき，νj ＞ 0 と並べておけば，次のようにまとめられます。
| 質量作用の法則 ［ネルンストの分配の法則］ 可逆的な化学反応式が，
と表されるとき， をこの化学反応の平衡定数として定義すると， が熱平衡状態において成り立つ。これを質量作用の法則と呼ぶ。ただし， であって，ΔrG0 は化学反応にともなう標準自由エネルギー変化と呼ぶ。 |
||||||||||||||||||||||||||||||
ここで，μj0＝μj0(T,P) である[#]ことに注意すれば，平衡定数は定数と言いながらも温度，圧力の関数であることを忘れてはいけません。（ここで導出の際に T，P を一定としたではないかと疑問に思う人は，関数 f＝xyz2 を x,y 一定の下で，zで微分した偏導関数 f’＝2xyz が x,y,z の関数であることを思い出せばよい。）また，ΔG0を標準自由エネルギー変化と呼ぶのは，約束ごととして温度，圧力を 25℃，１atm など標準条件と定めて，平衡定数などを報告，編集するよう推奨されているからです。 ( ⇒ ヘスの法則[#] 参照 ) その物理的な意味は標準条件において，化学量論比だけ用意された純粋な各出発物質の化学ポテンシャルと，１００％化学反応した後の化学量論比にある生成物の化学ポテンシャルとの差と考えることができます。
［１］ 質量作用の法則のもっとも重要な役目は化学平衡状態の予測にありますが，平衡状態にある系に摂動が加えられたときの緩和挙動についてもルシャトリエ-ブラウンの原理(LeChatelier-Braun’s law) と呼ばれる半定量的な指針を与えます。
高校生の時にも天下り的に教わる法則ですが，熱力学の基本原理に基づいて理解することができます。
| ルシャトリエ-ブラウンの原理 化学平衡状態にある系の条件，すなわち，温度，圧力，（組成) を変えるとそれを打ち消す方向に化学反応が進行する。 |
少し補足説明をしておきますと，ここに述べられている結論はその方向に化学反応がずっと続くという意味ではありません。新しい化学平衡状態に向かって状態変化が引き起こされると述べた方がより正確でしょう。
そして十分時間をかければ新しい平衡状態に達するはずです。また，「原理」と呼ばれていますが，熱力学の基本法則から必然的結果としてに導出することができます。
［２］
-組成(分圧) の変化に対する応答-
まず，この原理の具体例を見ておきます。水素，窒素からアンモニア蒸気の生成反応，
3H2 ＋ N2 →
←2NH3
において，ある組成の下で化学平衡にあって，
K(T,P)＝ xNH32 xH23 xN2
が成り立っているとします。そこへ等温定圧の下でアンモニア分子が加えられると，その直後は平衡から外れた状態となります。ところが，負の方向への逆反応が引き起こされ, アンモニア分子の一部が消費されて減少する一方で，水素分子，窒素分子が増加し始めます。そして十分時間が経過すると，質量作用の法則を満たす平衡状態へ到達し，巨視的な変化が見られなくなります。（下図）つまり，アンモニア分子の増加を打ち消すような反応をともない系が新たな平衡状態へ移動することが観察されるのです。
このような緩和現象を一般化し，法則として述べたものがルシャトリエ-ブラウンの原理です。アンモニア分子(ガス) を新たに添加する場合は，平衡定数そのものが変化するわけではありません。
 |
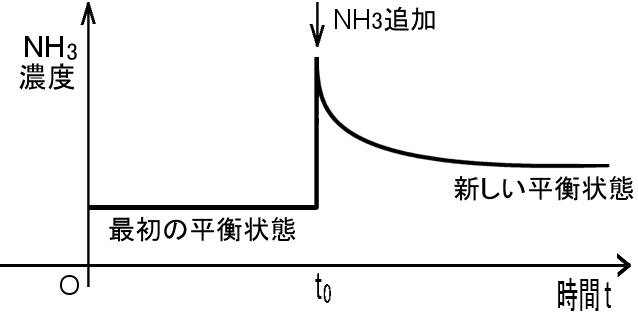| 窒素，水素，アンモニアからなる混合系にアンモニアを加えたときの アンモニアの緩和挙動。 |
［３］
-圧力(全圧) の変化に対する応答-
平衡定数 [#] は定数と言いながらもμj0＝μj0 (T, P) であることから，温度，圧力依存性があります。したがって，温度や圧力を変化させると平衡定数が変化し，その結果として，系の状態も新しい均衡点に向かって移動します。まず，その圧力依存性について調べてみます。
この場合の”圧力”とは系の全体にかかる圧力のことで，全圧と呼ばれることがあります。先程述べたような特定の成分を系に添加したときに見られる分圧 (〜組成) の変化とは違うことに注意してください。全圧の変化に対する系の応答を調べるために平衡定数 K(T, P) の圧力依存性について，その対数をとった，(計算が楽になります。)，
log K(T,P)＝− 1 νjμj0 RT
を次のように圧力に関して偏微分を行います。(理想気体として計算)
∂log K ＝− 1 νj ∂μj0 ∂P T RT ∂P T
↓ ∂μj0 T ＝ ∂ ∂G T,P T ＝ ∂ ∂G T T,P ＝ ∂V T,P ≡v~j0 ∂P ∂P ∂nj ∂nj ∂P ∂nj
＝− 1 νj･v~j0 RT
＝− ΔV0 [K-P曲線の傾き] ･･･[*] RT
ここで，ΔV 0 ≡
νj v~j0 は系が十分大きいとして，純物質の体積を基に計算される化学反応がδξ ＝
1 だけ正方向に進行したときの系の体積変化です。
したがって，この値がわかれば平衡定数の圧力依存性を求めることができるのです。定性的な議論に限れば，このΔV0 が正であれば，圧力の増加につれて平衡定数は減少することが[*] 式からわかります。
すなわち，生成物の量が減少する負方向への化学反応が引き起こされ，新たな化学平衡状態に向かうことがわかります。そして，負の方向へ化学反応が進んだ分だけ全体積は減少し，等温条件下では同時に圧力も減少するはずです。言い換えると，ΔV0 ＞ 0 である系に圧力を加えると，その加圧の効果が打ち消されるような方向に化学平衡点が移動すると述べることができます。
逆に系の圧力を減じれば，同様な推論から系の圧力を増加させるように化学平衡点が移動することも導かれます。この考察結果は，ルシャトリエ-ブラウンの原理と合致するものです。系がΔV0 ＜ 0 の場合も先程と全く逆のプロセスが引き起こされ，ルシャトリエ-ブラウンの原理が成り立つことを再び確認することができます。
［４］ 系の各成分が理想気体だけから構成されるならば，化学量論係数から系の圧力に対する応答を予測することもできます。理想気体の場合の標準化学ポテンシャルは純粋な j 成分にとることができて，v~j0 ＝V/nj＝ vj0 とできます。すると，
↓理想気体ならば，Pvj0 ＝RT
∂log K ＝− 1 νj･vj0 ∂P T RT
＝ − 1 νj [K-P曲線の傾き] P
ここで，右辺のνj は反応が正方向へ進行したときの系全体の粒子数の増減に対応しています。この符号を調べると平衡定数の圧力依存性(K−P
曲線の傾きの符号) がわかります。アンモニア蒸気生成反応に当てはめてみると，
Σνj＝ (−3−1＋2)＜0 であるため反応が正方向へ進むと全粒子数減少，つまり，K−P 曲線の傾きは正です。したがって，
[A] 圧力増加 ⇒ K(T,P)＝ ［NH3］2 が増加 ⇒ ［H2］2［N2］
［NH3］2が増加し，［H2］3［N2］が減少 ＝ 全粒子数減少 ⇒ 圧力減少
[B] 圧力減少 ⇒ K(T,P)＝ ［NH3］2 が減少 ⇒ ［H2］2［N2］
［H2］3［N2］が増加し，［NH3］2が減少 ＝ 全粒子数増加 ⇒ 圧力増加
すなわち，[A], [B] ともに，「圧力の変動の効果を打ち消す方向に平衡状態が移動する。」と述べることができ，ルシャトリエ-ブラウンの法則を確認できます。
(ここで，[A]＝xA という意味です)
すべての成分の化学ポテンシャルが理想系(理想気体) として振舞わない場合は，(3) 式が成立せず，ΔrG0 が使えません。そのときは直接ΔrG について，
∂ΔrG ＝ ∂ νjμj ∂P T ∂P T
＝ νj ∂μj ＝ νjv~j ･･･[**] ∂P T
| として，部分モル量を用いた ΔV~＝ | |
νjv~j の符号を評価することになります。 | |
ここで，ΔV~ は系が十分大きいとして，化学反応が正方向にδξ＝1 だけ進んだときの系の全体積変化を意味します。この符号の正負と圧力変化の方向によってどのような現象が引き起こされるか吟味を加えることで，理想系のときのνjvj 0 に対する議論と同様な結論を導くことができます。特に化学反応を伴う分子数の増減がゼロとなるケースでは[**] をそのまま用いた評価を行うことが必要です。
［５］
-温度の変化に対する応答-
最後に平衡定数K(T, P) の温度依存性を調べてみましょう。今度は，
| log K(T,P)＝− | 1 | |
νjμj0 |
| RT |
について圧力一定の下で温度に関する偏微分を計算します。
∂log K ＝− 1 νj ∂(μj0/T) ∂T P R ∂T P
↓ ∂(μj0/T) ＝−h~j0/T2＝−hj0/T2 なので，公式(19)を利用[#] ∂T P
＝ 1 νj･hj0 RT2
＝ ΔH0 RT2
ここで，
ΔH0 ＝ νj･hj0
は「ヘスの法則」で説明する標準 (反応) エンタルピー変化（＝反応熱）です[#]。ここで，ΔH 0 が負(系が受け取った熱量が負)，つまり，正反応が発熱反応である場合を考えてみると，今，導いた式から，K−T 曲線の傾きは負です。このときの温度変化に対する系の応答は，
|
温度増加 ⇒ K が減少 ⇒ 生成物減少＝逆反応(吸熱反応)進行 ⇒ 温度減少 |
すなわち，「温度の変動効果を打ち消す方向に平衡状態が移動する。」ことがわかります。
ΔH 0 が正の値を取る場合も同様の議論を経て同じ結論となり，そこでもルシャトリエ-ブラウンの法則が確かめられます。
化学ポテンシャルが理想系でない場合は，最後の"＝" で [#] 式 を用いて，
∂ΔG ＝ ∂ νjμj ＝ νj ∂μj ＝− νjs~j ∂T P ∂T P ∂T P
| として，ΔS~＝− | |
νjs~j を評価することになります。 | |
その結果，反応に伴うエントロピー変化が緩和を支配していることがわかります。
