| 2-1 複素1次関数 | ||
| f-denshi.com [目次へ]最終更新日:08/02/08 | ||
| サイト検索 | ||
[1] 複素関数とは,複素数zに複素数wを対応させる写像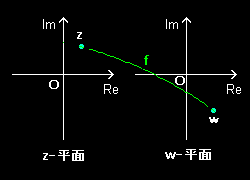
f: z → w=f(z)
です。成分で表示すると,
| z=x+i y → w=u(x,y)+i v(x,y) |
これは,複素数の1点zから複素数の1点wへの対応ですが,実質的には2つの実数の組(x,y)を2つの実数の組(u,v)を対応させる関数,
f:(x,y) → (u,v)
となっています。これは,複素関数は2次元ベクトルを2次元ベクトルに対応させる (=2次元ベクトル場 [#] ) 写像といってもよく,実際,ベクトル場と密接な関係を持っています[#]。この関数の振る舞いを一度に描こうとすると,定義域と値域に2本ずつ合計4本の座標軸が必要です。つまり,4次元の中にしか書くことができません。3次元ならば遠近法を使って2次元の紙面に書くことも可能ですが,4次元ではお手上げです。それでやむを得ず,上のように2枚の2次元平面 (z-複素平面=xy平面とw-複素平面=uv平面)を用いて関数の特徴を可視化することにしましょう。
[2] 何はともあれ,簡単な複素関数として1次関数と呼ばれるものをとりあげ,次の3タイプに分けて調べましょう。
(1) w=Az
(2) w=z+B
(3) w= 1 z
ここで,A,B は定数(∈複素数)です。複素関数は(ガウス)平面上の1点をもう一つの平面上の1点に移す写像と言いました。したがって,1点が1点に対応する様子を別々に図示しても点がただ2つあるだけでおしまいなので,ふつう,x-y平面内にある直線,円といった特徴のある図形が写像によって,u-v平面上でどのよう形に移されるのかを調べることで複素関数の基本的な特徴を把握します。
[3] w=Az の場合: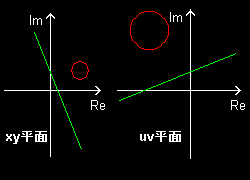
極座標で,A=Reiα,z=reiθとすれば,
⇒ w=Rrei (θ+α)
これは,ガウス平面内の回転と原点を源とする相似拡大(縮小)です。円は円,直線は直線に移ります。
[4] w=z+B の場合:
これは簡単で,タダの平行移動です。円は円,直線は直線に移ります。
| [5] w= | 1 | の場合: |
| z |
この写像を調べるには少し計算が必要です。最初にガウス平面上の直線と円の方程式を求めておきます。まず,xy平面内の直線の方程式は,
ax+by+c=0 a,b,c∈実数
ですが,ガウス平面上では,
実数成分 : x=(z+z*)/2
虚数成分 : y=i (−z+z*)/2
と対応するので,xy平面上の直線の方程式に代入してx,y を消去すれば,
[a/2−i b/2]z+[a/2+i b/2]z*+c=0
⇔
Az+A*z*+c=0 ・・・[*] : ただし,A=a/2−i b/2, A*=a/2+i b/2
という式になります。 一方,xy平面内の円の方程式は,
(x−p)2+(y−q)2−r2
=x2+y2−2px−2qy+p2+q2−r2=0, ただし,r≠0; p,q,r∈実数
ここで,zz*=x2+y2 に注意して,直線の方程式の導出と同様にx,y を消去すると円の方程式は,
zz*−Bz−B*z*+BB*−r2=0 ・・・[**] : ただし,B=p−iq,r≠0, ( BB*=p2+q2 )
と書くことができます。つまり,この関係を満たす複素数 zの集合はガウス平面上で半径r の円を描きます。以上で準備は終わり。
[6] [直線の像] そこで,直線[*]は写像 w=1/z によって,
A/w+A*/w*+c=0
に移されることがわかります。書き換えると,
cww*+A*w+Aw*=0
これを満たすwの集合が,z平面上の直線[*]に対応するのw-平面上の像となります。なお,この式の意味は場合分けして吟味する必要があります。
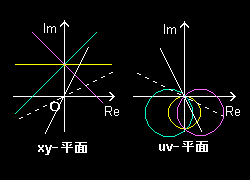 ケース1 c=0 のとき ←直線が原点通るとき
ケース1 c=0 のとき ←直線が原点通るとき
A*w+Aw*=0
これを uv-平面の成分で表すと, ← w=u+iv ですね
(a/2+ib/2)(u+i v)+(a/2−ib/2)(u−iv)=0
⇔
au−bv=0 [原点を通る直線]
ケース2 c≠0のとき, ←原点通らない直線のとき
cww*+A*w+Aw*=0
uv平面では,
c(u2+v2)+[a/2+i b/2](u+i v)+[a/2−i b/2」(u−iv)
=c(u2+v2)+au−bv=0
⇔
(u+a/2c)2+(v−b/2c)2=(a2+b2)/4c2 [原点通る円]
すなわち,z平面上で直線となる複素数の集合は,写像w=1/zによって,
(1) 原点を通る直線は,原点を通る直線へ
(2) 原点を通らない直線は,原点を通る円へ
写されることが分かりました。
[7] [円の像] 次に円は写像:w=1/zによって,
(1/w)(1/w)*−B(1/w)−B*(1/w)*+BB*−r2=0
すなわち,
1−Bw*−B*w+(BB*−r2)ww*=0
この方程式も場合分けして調べます。
ケース1 BB*−r2=p2+q2−r2=0のとき,←原点通る円のとき
1−Bw*−B*w
=1−(p−i q)(u−i v)−(p+i q)(u+i v)
=1−2pu+2qv=0 [直線]
ケース2 BB*−r2=p2+q2−r2≠0のとき,←原点通らない円のとき
1−Bw*−B*w+(BB*−r2)ww*
=1−2pu+2qv+(p2+q2−r2)(u2+v2)=0
⇔
[u−p/(p2+q2−r2)]2+[v+q/(p2+q2−r2)]2−r2/(p2+q2−r2)2=0 [円]
[8] 以上まとめると
|
|||||||
| z-(x,y)平面 | w-(u,v)平面 | ||||||
| 直線 | 原点通る直線 ax+by=0 |
f ⇒ |
原点通る直線 au−bv=0 |
||||
| 原点通らない直線 ax+by+c=0 [c≠0] |
原点通る円 (u+a/2c)2+(v−b/2c)2=(a2+b2)/4c2 |
||||||
| Az+A*z*+c=0; ( A=a/2−i b/2 ) |
cww*+A*w+Aw* | ||||||
| 円 | 原点通る円 x2+y2−2px−2qy=0 |
f ⇒ |
原点通らない直線 1−2pu+2qv=0 |
||||
| 原点通らない円 (x−p)2+(y−q)2−r2=0 [p2+q2−r2≠0] |
円 [u−p/(p2+q2−r2)]2+[v+q/(p2+q2−r2)]2 =r2/(p2+q2−r2)2 |
||||||
| zz*−Bz−B*z*+BB*−r2=0; ( B=p−i q, r≠0 ) |
1−Bw*−B*w+(BB*−r2)ww*=0 ( BB*−r2=p2+q2−r2 ) |
||||||
[9] ここでの考察を一つにまとめた次式で一般化される関数,
| w= | Az+B |
| Cz+D |
を1次関数(または,1次分数関数)と呼びます。この関数は先の3つの要素的な関数の合成関数として表せることに注意して下さい。 以上の具体的な計算を念頭において,円円対応,リーマン球面,等角写像などの複素関数の特徴について書かれた教科書を読めば理解が得られるのではないのでしょうか。本講義のAppendix [#] にも簡単に説明しておきました。