
 |
10 留数定理 | |
| f-denshi.com [目次へ] 最終更新日: | ||
| サイト検索 | ||
[1] 領域D の一点a を除いた領域Daで正則な関数 f(z)を 特異点a のまわりでローラン展開,
| f(z)=・・・+ | c-n | +・・・+ | c-2 | + | c-1 | +c0+c1(z−a)+c2(z−a)2+・・・+cn(z−a)n+・・・ |
| (z−a)n | (z−a)2 | z−a |
したときの(z−a)-1項の係数c-1,すなわち,
c-1= 1 f(z)dz (留数) 2πi
を留数と呼んで,Res[f(z),a] と表します。
c-1 に留数という特別な呼び名がついているのは,関数をaのまわりでローラン展開してから項別に単一閉曲線C に沿って積分すると,値が0とならない項は (z−a)-1 の項だけだからです。つまり,
留数を求めることは,複素関数 f(z)の積分値を求めることに等しい。
のです。具体的に書くと,複素関数 f(z)の積分は留数を用いて,
f(z)dz=2πi c-1
となります。
[2] これは,容易に単一閉曲線C に囲まれた領域に有限個の孤立特異が存在する場合に拡張され,次の定理となります。
| [ 留数定理 ]
単一閉曲線C に囲まれた領域において複素関数f(z)が有限個の孤立特異点 a1,a2,・・・,an を除いて正則であるならば,
が成り立つ。ただし,Res[f(z),ak] は孤立特異点 ak の留数。 |
[3] 具体的に留数を求める方法を考えます。
(1) a が除去可能な特異点の場合,Res[f(z),a] = 0 です。
(2) a が真性特異点の場合は,f(z) のローラン展開を求めて,c-1 を算出する。
(3) a がm位の極であるときは, ←この場合が取り合えず重要です。
f(z)= c-m ・・・+ c-2 + c-1 +c0+c1(z−a)+c2(z−a)2+・・・ (z−a)m (z−a)2 z−a
と展開されるので,f(z) に (z−a)m をかけると,
(z−a)mf(z)=c-m+c-m+1(z−a)+・・・+c-1(z−a)m-1+c0(z−a)m+・・・
[4] これを m−1 回微分すると,
| dm-1 | (z−a)mf(z) | =(m−1)!c-1 +m(m-1) ・・・ 2c0(z−a) +(m+1)m ・・・ 3c1(z−a)2 +・・・ |
| dzm-1 |
両辺 (m−1)!で割って, z→a とすれば,(z−a)のベキ項(右辺の第2項以下)は → 0 となるので,
1 dm-1 (z−a)mf(z) =c-1 (m−1)! dzm-1
[5] まとめると
| 留数の値 (計算方法) Res[f(z),a] = (1) 0 [ a は除去可能な特異点 ] |
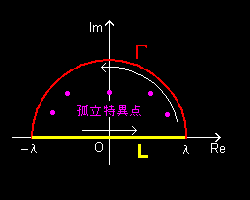 [1] 単一閉曲線C(=L+Γ)の経路の一部分(L)が右図のように実数軸上にある場合,その内部に有限個の孤立特異点 a1,a2,・・・,an だけしか含まないならば,留数定理[#]から,
[1] 単一閉曲線C(=L+Γ)の経路の一部分(L)が右図のように実数軸上にある場合,その内部に有限個の孤立特異点 a1,a2,・・・,an だけしか含まないならば,留数定理[#]から,
f(z)dz=2πi Res[f(z),ak]
が成り立ちます。積分経路を図のように L と Γ の二つに分けて考え,L 上の積分は普通の実数関数の積分と違いがないことに注意すれば,上の式は,
f(x)dx=− f(z)dz+2πi Res[f(z),ak]
と書くことができます。左辺の変数記号は実数上の積分であることを示すために x と書き換えてます。
[2] ここで,λ→∞ のときを考察します。もし,右辺の第一項が 0 に収束する,すなわち,
f(z)dz=0
ならば,実数上の広義積分が,
f(x)dx=2πi Res[f(z),ak]
として留数を用いて表せることがわかります。
[3] では,具体的にこの方法で広義積分が求められる例をみてみましょう。求めるべき積分は,
1 dx x2+1
です。被積分関数は前章でローラン展開の例 [#] に用いた関数と同型で,x→z とし,複素関数とみなせば,一位の極を±i にもっており,特に孤立特異点(+i ) のまわりで,
f(z)= 1 = 1 − 1 + (z−i) −・・・ z2+1 2i (z−i) (2i )2 (2i )3
のように展開できるということでした。したがって,Res[f(z),+i ]=1/2i です。ここで,λとして1より大きくとれば,この孤立特異点だけを含む右図のような単一閉曲線(L+Γ)を複素平面上で考えることが可能です。
[4] そして,「f(z)のΓ上の積分が0である」ならば,
1 dx=2πi Res[f(z),+i ] =2πi /2i =π ・・・[答え] x2+1
と求められるのです。
[5] さて,半円周:Γ上の積分の見積もり(=0)ですが,次の命題を利用します。
|
関数f(z)について,複素平面上で原点を中心とする半径λ,(0≦θ≦π)の半円周:Γ上で,ある正数 M が存在して, |f(z)|≦Mλ−P ( P>1 ) ならば,
|
[証明]
dz = i λeiθdθ と変数変換して次の積分を考えると,
| f(z)dz|≦ |f(z)||dz| ≦ Mλ1-P | eiθ | dθ=π Mλ1-P
したがって,λ→∞ とすれば,1−P < 0 よりλ1-P→ 0 なので,
f (z) dz = 0
証明終
[6] この命題を用いるために f(z) を λ2 >> 2 で、次のような不等式が成り立つことを示します。
|f(z)|= 1 ≦ 1 = 1 < 2 |z2+1| |z|2−1 λ2−1 λ2
この結果,f(z)のΓ上の積分は,λ→∞ で 0 であることが言え,[答え]が最終的に確認されました。
[7] この問題では半円周上の積分が0であることから留数を利用して簡単に広義積分が求められましたが,半円周上の積分値が 0 とならない場合でも次のように積分値を求められる場合があります。
|
関数f(z)について,複素平面上で原点を中心とする半径λ,(0≦θ≦π)の半円周:Γ上である正数 M が存在して, |f(z)|≦Mλ−P ( P>0 ) ← Pが 1 ではなく 0 より大きいことに注意! ならば, で,コーシーの主値を用いて,
|