
 |
9 ローラン展開 | |
| f-denshi.com [目次へ]最終更新日: 05/07/18 | ||
| サイト検索 | ||
[1] 孤立特異点
f(z)が領域D 上では正則でないが,D の一点a を除いた領域 Da で正則なとき,「a を f(z)の孤立特異点」といいます。例えば,
f(z)= 1 , n=1,2,・・・ (z−a)n
は,a では値を持ちませんがこの点を除く複素平面上のすべての点では正則なので孤立特異点となります。この関数はa でテーラー展開できません。しかし,よくみると,f(z)=(z−a)-n はテーラー展開を拡張してマイナスのベキまで許した場合の整級数展開の -n 番目の項とみることもできるではありませんか。
[2] 孤立特異点のまわりのローラン展開
孤立特異点のまわりではテーラー展開はできませんがマイナスのベキ級数も用いるとテーラー展開モドキの表現が可能なのです。この表示方法をローラン展開と言います。マイナスのベキまで駆使して展開するのはテーラーの展開の拡張という意味合いもありますが,このように展開する本当のメリット(関数f(z)の積分に役立つ)は次ページに進むと判明します。とりあえず,ここではローラン展開とは何か説明しましょう。
ローラン展開
特に,n=-1のときは,
|
積分経路 C を右図のようにPを始点とし,C = C1+L−C2-L ( L=P→Q ) に取れば,C の囲む領域 D で f(z) は正則です。そこで,この領域についてコーシーの積分公式を用いれば,(
線分 PQ 上の積分はキャンセルされて0 )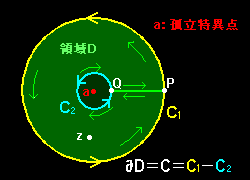
| f(z)= | 1 | f(t) | dt | |
| 2πi | t−z |
| = | 1 | f(t) | dt+ | 1 | f(t) | dt | ||
| 2πi | t−z | 2πi | t−z |
= g+(z) + g-(z)
と2つの積分を計算することになります。積分の中はテーラー展開を考えたときと同じように[#]
f(t) = f(t) dt t-z (t−a)−(z−a)
と変形しておき,
(1) C1上を動くとき
r ≡ z−a <1 なので, t−a
g+(z) = 1 f(t) dt 2πi (t−a)(1−r) 積分と極限の順番を変えて,(←とりあえずここでは認めることにします。)
= 1 f(t) (1 + r + r2 + ・・・ )dt 2πi (t−a)
= 1 f(t) dt ・(z−a)n 2πi (t−a)n+1
(2) C2上を負の方向動くとき,
r' ≡ t−a <1 として, ←こんどは先程と分母・分子を入換えてます。 z−a
g-(z) = 1 - f(t) dt 2πi (1−r')(z−a)
= 1 - f(t) (1 + r' + r'2 + ・・・ )dt 2πi (z−a)
= 1 f(t) t−a n dt 2πi (z−a) z−a ↓ n を 0 からでなく 1 からに付け替えて
= 1 f(t)(t−a)ndt 1 2πi (z−a)n+1
= 1 f(t)(t−a)n-1dt 1 2πi (z−a)n
となり,マイナスのベキの項を与えます。
[3] f(z) = g+(z)+g-(z) を表記するとき n の和に関して,共通のn,つまり,マイナスのベキ項の和は n = -1,-2,-3,・・・とすることにすれば,
| f(z) = | cn(z−a)n | |
| =・・・+ | c-n | +・・・+ | c-2 | + | c-1 | +c0+c1(z−a)+c2(z−a)2+・・・+cn(z−a)n+・・・ |
| (z−a)n | (z−a)2 | z−a |
cn = 1 f(z) dz (n=・・・-2,-1,0,1,2,・・・) 2πi (z−a)n+1
と書くことができます。
| [1] 例として, f(z)= | 1 | を考えて見ましょう。 |
| z2+1 |
この関数は後ほど留数の計算例 [#] としても利用します。まず,次のように変形すると,
f(z)= 1 1 (z−i) (z+i)
1位の極を +i と -i にもっていることが分かります。一般論で述べたように複素平面上のある点を中心とするいくつかの円によって正則な領域を閉曲線として囲み出せる(ただし,閉曲線には向きがあることに注意)ことがその点でローラン展開ができる条件となります。この関数の場合,2つの極 ±i を含まないような領域を囲み出す必要があるのです。すると, +i の周りの展開を考える場合,右下の図のような2通りA,B (正則な領域は緑色で示しています)が考えられます。
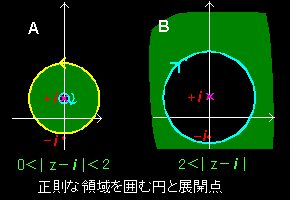 [2] 特異点 +i の周りの展開は半径がε,r (0<ε<r<2なる2つの円はさまれた領域が正則であることから,
[2] 特異点 +i の周りの展開は半径がε,r (0<ε<r<2なる2つの円はさまれた領域が正則であることから,
A : f(z), 0<|z−i|<2 は z=+i の周りに展開できる。
ことがわかります。展開したときには,閉曲線の正方向のループ線積分(黄色)から正のべき項の存在,負方向のループ線積分(水色)からマイナスのべき項の存在が予想できます。
[3] 展開項の係数は定義式にしたがって計算することもできますが,実践的には式を適切に変形して直接求めます。そのときに重宝するのが次の公式です。
| 公式: | 1 | =1+r+r2+・・・+rn+・・・・, |r|<1 ←この公式は非常に重要! |
| 1−r |
早速,これを用いて計算してみましょう。
f(z)= 1 1 = 1 1 (z−i) (z−i+2i) (z−i) 2i {1+(z−i)/2i }
0<|z−i|<2 のとき,公式 で r =−(z−i )/2i を適用して,
f(z)= 1 [ 1−(z−i)/2i +{(z−i)/2i }2−{(z−i)/2i }3 ・・・・ ] 2i (z−i)
すなわち,ローラン展開は,
| 1 | = | 1 | − | 1 | + | (z−i) | − | (z−i)2 | + ・・・・ [答A] |
| z2+1 | 2i (z−i) | (2i )2 | (2i )3 | (2i )4 |
[4] +i の周りでは,半径 r = 2 のときに円周上にもうひとつの極 -i があるために展開を行なうことはできません。しかし,r >2 であるならば,その円周の外側ではf(z)は正則なので,
B: f(z),|z−i|> 2 はz=+i の周りに展開できる。
ことがわかります。ただし,この領域を囲むためには閉曲線を負の方向に回る必要があるので,この領域における展開項にはマイナスのべき項だけが存在するはずです。実際に,
f(z)= 1 1 = 1 1 (z−i) (z−i+2i) (z−i) (z−i){1+2i /(z−i)}
2<|z−i|のとき,公式 で r =−2i /(z−i ) を適用して,
= 1 [ 1−2i /(z−i)+{2i /(z−i)}2−{2i /(z−i)}3 ・・・・ ] (z−i)2
= 1 − (2i ) + (2i )2 − (2i )3 + ・・・・ [答B] (z−i)2 (z−i)3 (z−i)4 (z−i)5
となり,負のべき項で展開されています。
[5] たいていローラン展開は極の周りで行なうものですが,必ずしも極だけでしか展開できないというわけではありません。次に極でない点として,+2i でのローラン展開を考えて見ましょう。この場合,右図を参照すればれば,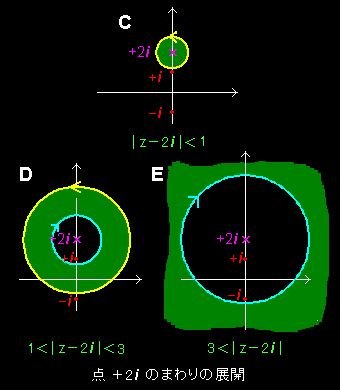
(C) 0<|z−2i|<1
(D) 1<|z−2i|<3
(E) 3<|z−2i|
の3つの領域でも展開可能なことがわかります。そして,
(C)は正のべき項だけ(テーラー展開可能ということ),
(D)は正負両方のべき項,
(E)は負のべき項だけ
から展開式が構成されるだろうことが予想されます。
[6] ここでは(D)の場合について計算してみましょう。
D : f(z),1<|z−2i|<3 は z=+2i の周りに展開できる。
| f(z)= | 1 | 1 | − | 1 | ||
| 2i | (z−i) | (z+i) |
= 1 1 − 1 2i (z−2i+i) (z−2i+3i)
= 1 1 − 1 2i (z−2i){1+i /(z−2i)} 3i{1+(z−2i)/3i}
ここで,Dの領域では,|i /(z−2i)|<1,および,|(z−2i )/3i|<1 なので,先の公式 を用いて,
= 1 1 [1−i /(z−2i)+{i /(z−2i)}2−{i /(z−2i)}3+ ・・・・] 2i (z−2i)
− 1 [1−(z−2i)/3i +{(z−2i)/3i }2−{(z−2i)/3i }3 +・・・・] 3i
| = ・・・+ | i 2 | − | i | + | 1 | ||
| 2i (z−2i)3 | 2i (z−2i)2 | 2i (z−2i) | |||||
| − | 1 | + | (z−2i) | − | (z−2i)2 | + | (z−2i)3 | − ・・・ |
| 2i ・3i | 2i (3i )2 | 2i (3i )3 | 2i (3i )4 |
・・・ [答D]
[1] ローラン展開のようすに基づいて孤立特異点を分類します。次の3種類あります。
| (1) 除去可能な特異点 |
|
|||
| (2) m位の極となる特異点 |
|
|||
| (3) 真性特異点 |
|
ここで,m,n自然数です。言い換えるとf(z)をaでローラン展開したときに,
(1) マイナスベキの項をまったく含まない
(2) マイナスベキの項を有限個だけ含む
(3) マイナスベキの項を無限個含む
(1)の場合,孤立特異点aにおけるf(z)の値を適当に定めてやる,すなわち,f(a)=b とおくことで,領域Da 上の正則関数をD上の正則関数に拡張することが可能です。また,有限の領域に極以外の特異点をもたない関数を有理型関数といいます。
追加
|
定理 (1) f(z)が単一閉曲線Cに囲まれた領域Dの一点aにおけるp位の極を除いて正則とする。また,領域Dの一点bにおいてn位の零点を持つがC上では零点を持たないとする。このとき,
が成り立つ。 この結果は極,零点が複数個ある場合に拡張することができ, (2) f(z)が領域Dにおいて,位数が,p1,p2,・・・,pj であるj個の極,a1,a2,・・・,aj をもち,また,k個の位数が,n1,n2,・・・,nkである零点,b1,b2,・・・,bkをもち,C上に零点を持たないとする。このとき, N=n1+n2+・・・+nk とすれば, が成り立つ。 |