
 |
8 複素関数のテイラー展開 | |
| f-denshi.com [目次へ]最終更新日:21/09/08 極限と積分の交換に証明を与えた | ||
| サイト検索 | ||
複素関数は,1回微分できれば何回でも微分ができ,テーラー展開もできる。正則関数と呼ばれる所以である。
[1] 複素関数も実数の場合と同じようにテイラー展開ができます。
| 定理 点a を中心とする半径R の円C の内部(=領域D )で正則な関数f(z)は,D内の点z において,a の周りに次のようにテイラー展開できる。
|
[証明]
(1) 証明のポイントは,|r|<1 のときに成り立つ次の整級数公式,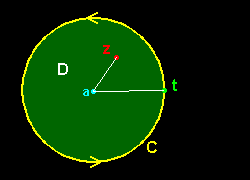
1 = 1+r+r2+・・・+rn+ ・・・・ = rn 1−r
および,
(2) コーシーの積分公式 [#] です。これを,
f(z)= 1 f(t) dt 2πi t−z
= 1 f(t) dt 2πi (t−a)−(z−a)
= 1 f(t) dt 2πi (t−a)(1−r)
と変形します。 ただし,
r = z−a t−a
です。
[2] ここで,|r|<1 なので(1)を用いて,
f(z)= 1 f(t) ・rn dt 2πi (t−a)
= 1 f(t) z−a n dt 2πi (t−a) t−a
さらに,積分と極限の順番を変えて,( ⇒ Appendix3 に証明があります。)
↓ n階微分の積分表示 [#] より,
= 1 ・ n! f(t) dt (z−a)n n! 2πi (t−a)n+1
= 1 f(n)(a) (z−a)n n!
が得られます。
[3] 結果だけみると,複素数のテイラー展開の式は見かけ上,実数のテイラー展開の場合と比べて実数で使う記号 x をただ、 x ⇒ z と置き換えただけです! しかし、実数のテイラー展開[#] と違うことは,関数f(x) に関して無限階微分可能をあらかじめ仮定していないということです。ここでの仮定は、複素関数f(x) の正則性です。つまり、複素関数f(x) の場合,考えている領域で一回微分可能という条件からf(x) が整級数展開できるということが導かれているのです。これは,
複素関数は、1回微分できれば何回でも微分ができ,テーラー展開もできる。
ということを意味しています。実数関数の場合はこんなことは言えませんでしたね⇒[#] 。実数は1回微分ができても数回目に微分ができなかったり,無限回微分ができてもテーラー展開可能とは限らないのでした[#]。
これも複素関数と実関数に関する見かけ上は同じ定理でも,その中身はまったく違うという例[#] です。
最後,用語だけの問題ですが,解析関数という用語もしばしば使われます。解析的という言い方もしますが,ある領域(ある点のε近傍)で解析関数であるとは,その領域でその関数が収束ベキ級数で表せることをいいます。したがって,複素関数では,「解析関数=正則関数」と考えて問題ありません。しかし,実数関数では,1回どころか無限回微分可能でも解析関数でないことがある [#] ので,「解析関数」とは非常に強い制限と考えられます。