 |
203 フーリエ変換 |
|
| f-denshi.com 更新日: |
1.フーリエ変換
[1] 周期2Lを持つ関数の複素関数形式のフーリエ級数展開は,
| f(x)= |
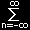 |
cnexp(i nπx/L), ・・・・ [*] |
| cn = |
1 |
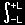 |
f(x)exp(−i nπx/L )dx ・・・・ [**] |
|
| 2L |
となります[#]。ここで,[**] は,
| cn = |
π |
・ |
1 |
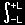 |
f(x)exp(−i nπx/L )dx |
|
|
|
|
|
 |
2π |
L |
|
|
|
 |
2π |
|
と書き表せることに注意して,変数変換,
および,関数の定義,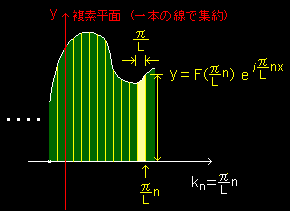
| F(kn) ≡ |
1 |
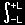 |
f(x)exp(−i knx )dx ・・・・(1) |
|
|
|
 |
2π |
|
を行なうと,
| cn = |
π |
・F(kn) |
|
|
|
|
 |
2π |
L |
|
| f(x)= |
1 |
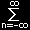 |
π |
・F(kn)exp(i knx) ・・・(2) |
|
|
|
|
 |
2π |
|
L |
と書き改められます。
[2] ここで,L → ∞ を考えると,(2)の級数和は関数:F(k)exp(i kx)の刻み幅を (π/L)とした(広義の)リーマン積分の定義[#]そのものズバリであることに気がつきます(右上図)。
(もし,わかりにくければ,F(kn)exp(i knx)=F(kn)cosknx+i F(kn)sinknx として,F(kn)cosknx,+i F(kn)sinknx とばらしてから積分を考えよ。)
すなわち,積分記号を用いて,
| f(x)= |
1 |
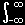 |
F(k)exp(i kx)dk ・・・・・ (2)’ |
|
|
|
 |
2π |
|
と書くことができます。さらに(1)は, L→∞ の極限における kn を連続な実数とみなし,k と簡単に記述すれば,
| F(k)= |
1 |
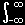 |
f(x)exp(-i kx )dx ・・・・・ (1)’ |
|
|
|
 |
2π |
|
この(1)’をフーリエ変換 F : f(x) ⇒ F(k) ,(2)’を逆フーリエ逆変換 F -1: F(k) ⇒ f(x) といいます。
以上の説明からわかるように,
フーリエ変換 F とは,
⇒ 与えられた関数f(x)から,フーリエ係数を求めること。
逆フーリエ変換 F -1 とは,
⇒ 与えられたフーリエ係数から関数f(x)を求めること。 |
に対応しています。
以上,大雑把ですがフーリエ級数展開とフーリエ変換がどのような関係になっているか示しました。
以上の議論は容易に3次元に拡張でき,
2.フーリエ変換の基本公式
[1] f(x),f1(x),f2(x)のフーリエ変換をそれぞれ,F(k),F1(k),F2(k)とし,a,b を定数とすれば,
|
元の関数f(x) |
関数のフーリエ変換F(k) |
| (1) |
f(-x) |
F(-k) |
| (2) |
af1(x)+bf2(x) |
aF1(k)+bF2(k) |
| (3) |
f(x−a) |
e-iak・F(k) |
| (4) |
f(ax) |
|a|-1・F(k/a) |
| (5) |
eiak・f(x) |
F(k−a) |
| (6) |
xn・f(x) |
 |
i |
d |
 |
n |
F(k) |
|
|
| dk |
|
|
| (7) |
f(n)(x) [n階微分] |
(ik)nF(k) |
| (8) |
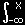 |
f(x) dx |
|
|
|
|
が成り立ちます。
3.フーリエ変換の計算例
|
元の関数 f(x) |
フーリエ変換 F(k) |
| (1) |
|
| exp |
 |
−π2k2r2 |
 |
|
| (2) |
|
| exp |
 |
−2π|k|r |
 |
|
| (3) |
|
|
exp |
 |
|
 |
|
|
| (4) |
|
|
| (5) |
|
|
[目次へ]
