 |
251 ラプラス変換 |
| f-denshi.com 更新日: |
1.ラプラス変換
[1] f(x) の次の積分(広義積分)をラプラス変換と言います。
 |
e-st・f(t)dt |
= F(s) |
|
積分結果を変数 s の関数とみなせば、これは、関数、f(t)を関数 F(s) に対応させる汎関数で、
L : f(t) ⇒ F(s)≡L[f(t)]
と考えることができます。
[2] 具体的にいくつか計算してみましょう。
(1) f(t)=A [定数]の場合
 |
e-st・A dt |
= A/s =F(s) |
(2) f(t)=e-at の場合、
 |
e-st・e-atdt |
= |
 |
e-(s+a)tdt |
| = |
 |
-e-(s+a)t |
 |
∞ |
= |
1 |
|
|
|
| s+a |
0 |
s+a |
[3] その他、よく使うラプラス変換をいくつかを下にまとめておきます。
| f(t) |
L[f(t)]=F(s) |
| c (定数) |
|
| t |
|
|
|
|
| 1 |
|
|
|
 |
πt |
|
|
| 1 |
|
|
|
 |
s |
|
|
|
|
| 1 |
|
|
|
 |
s3 |
|
|
|
|
1/sn (n>0) |
| exp{-at} |
1/(s+a) |
|
a |
・exp |
|
|
|
|
 |
4πt3 |
|
|
|
|
|
| exp{-a |
 |
s |
} |
|
| 1 |
|
|
|
|
 |
πt |
|
|
|
|
|
| exp{-a |
 |
s |
|
|
|
|
 |
s |
|
|
| erfc{ |
a |
} |
|
|
|
 |
4t |
|
|
|
|
|
| exp{-a |
 |
s |
} |
|
| s |
|
| δ(t-a): デルタ関数 |
exp{-as} |
| H(t-a): ヘビサイド関数 |
|
2.公式
[1]ラプラス変換を用いた微分方程式の解法に役立つ公式をいくつか述べておきましょう。
証明:
| L[f'(t)]= |
 |
e-st・f'(t)dt |
=[e-st・f(t)] |
∞ |
− |
 |
(-s)e-st・f(t)dt |
| 0 |
| −f(0)+s |
 |
e-st・f(t)dt |
=−f(0)+sF(s) |
|
[2] f''(t)についても部分積分を2回繰り返して、
| L[f''(t)]=s2F(s)−sf(0)−f'(0) |
を示すこともできます。
[3] その他の重要な公式をまとめておきましょう。
| g(x) |
L[g(x)] |
| f'(t) |
sF(s)−f(0) |
| f''(t) |
s2F(s)−sf(0)−f'(0) |
| af(at) |
F(s/a) |
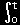 |
f(t)dt |
|
|
F(s)/s |
| f(t)・exp{at} |
F(s-a) |
| Uヘビサイド(t-a)= |
 |
f(t-a) t>a |
| 0 t<a |
|
exp{-as}f(s) |
ラプラス変換がなぜ微分方程式の解法に役立つかと言えば、上の公式たちを用いて変数を
t から s に変換すると、微分・積分記号が消えて、未知数 s に関する代数方程式を解くことに問題を置き換えられるからです。その代数方程式の解を逆ラプラス変換で変数
t の関数に戻してやればそれが解くべき微分方程式の解となるわけです。具体的な効用は後ほど拡散方程式の解法[#]の中で示します。
[目次へ]