| 252 ラプラス変換のたたみ込み | |
| f-denshi.com 更新日: 執筆中 | |
| 畳に込み(コンボリューション)の定理
定義: 関数 f(t)と g(t)が与えられたとき、合成積 f*g を、
と定義すると、それぞれの関数のラプラス変換を、 L[f(t)]=F(s)、 L[g(t)]=G(s) とすれば、 L[f*g(t)]=F(s)G(s)が成り立つ。 |
証明: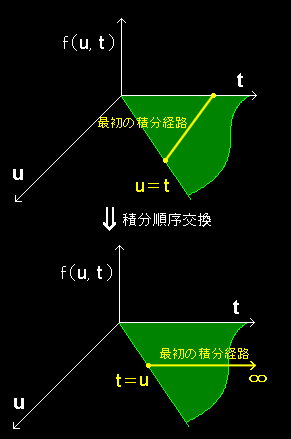
L[f*g(t)]= e-st・f*g(t)dt
= e-st・ f(t−u)g(u)dudt
ここで、積分の順番を入れ換えれば、
= e-st・f(t−u)g(u)dt du
さらに、t-u = w と置換すれば、( 変数 t → w に変換 )
= e-s(w+u)・f(w)g(u)dw du
= e-sw・f(w)dw e-su・g(u)du =F(s)・G(s)
「たたみ込み」の考え方を,「離散的なたたみ込み」の例で説明します。
各時期に原発から放出された放射能が,
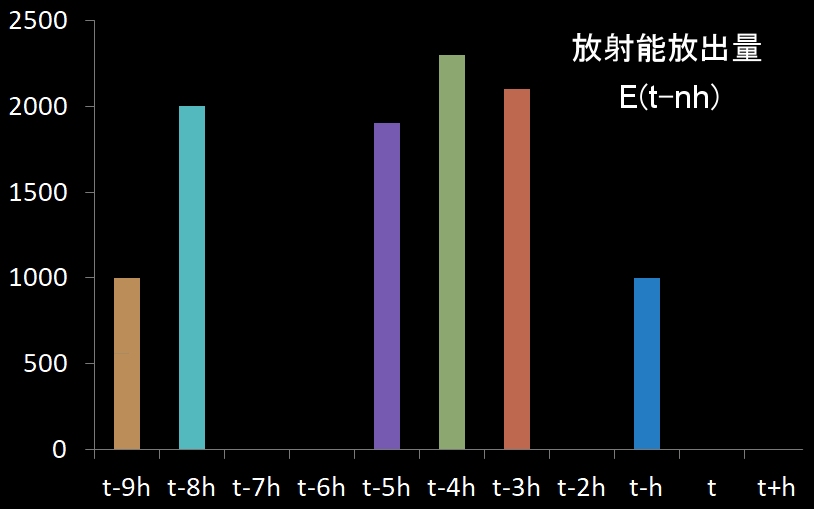
であることが分かっているとします。横軸は年代です。そして,放射能の半減期が h であるとする,すなわち,下図,
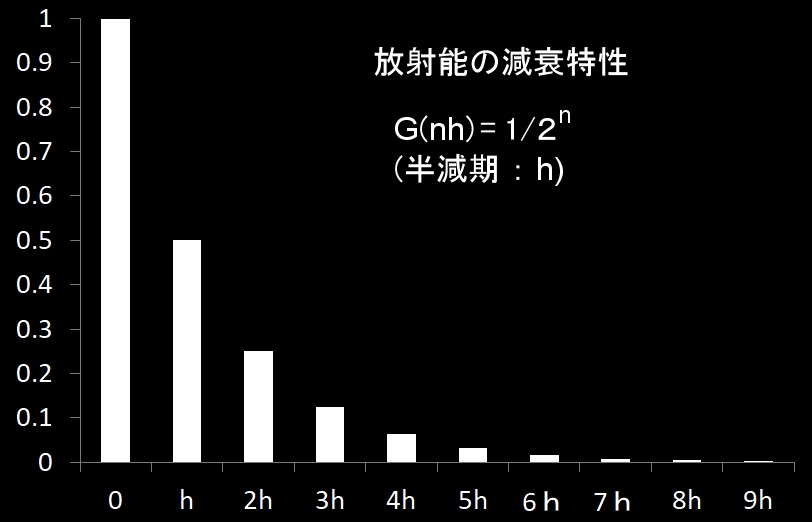
で放射能の減衰特性(応答関数)が与えられるとします。
このとき,t 年に存在する放射能は,下図の赤い囲みの中の放射能量を加算すればよいのですが,
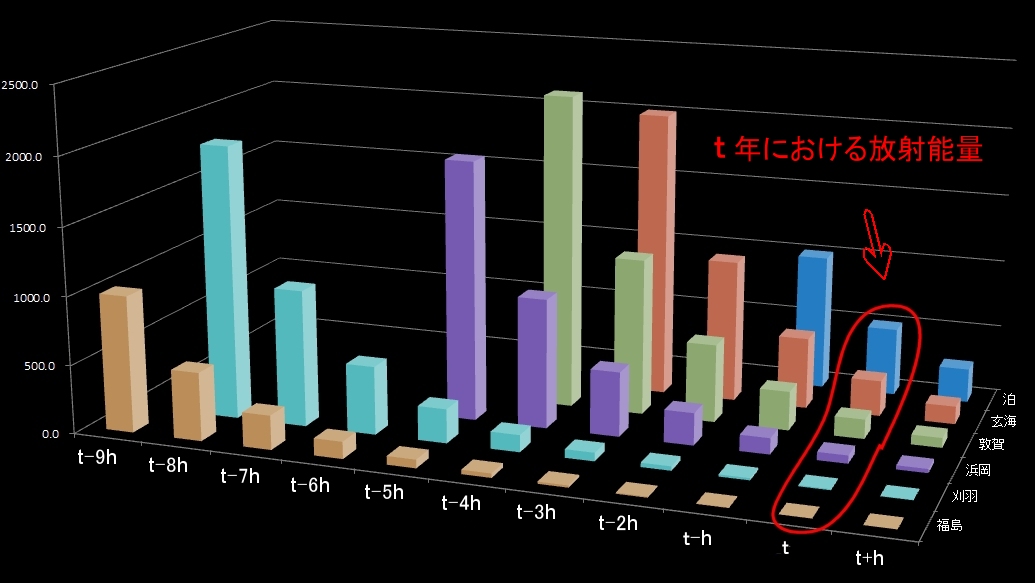
その放射能P(t)の計算式は,
P(t)=E(t−9h)G(9h)+E(t−8h)G(8h)+E(t−5h)G(5h)
+E(t−4h)G(4h)+E(t−3h)G(3h)+E(t−h)G(h)
= E(t−nh)G(nh)
と表記することができます。( n>10のとき,E(tーnh)=0 )
この離散的な関係式の連続的な極限を考えたものが,たたみ込み積分であって,
P (t) = E ( t−τ)G(τ)dτ
と書き表すことができます。G(τ)は各イベント(事象)が起きてからの減衰を表すので,τ<0 ではゼロの値をとる関数です。また,積分区間が-∞<τ<∞ となっていますが,これはフーリエ変換も利用できるように,形式的に積分範囲を広げただけでそれ以上の意味はありません。