461   デルタ関数とステップ関数
f-denshi.com  更新日：

　１．δ関数いろいろ

［１］　デルタ関数の定義からです。次の２つの条件を満たすような関数を(ディラックの)デルタ関数，δ(x)と書きます。

(１)　δ(x) ＝ ∞　　(x＝0) 0　　  (x≠0) 　(２)　 δ(x)dx ＝ 1

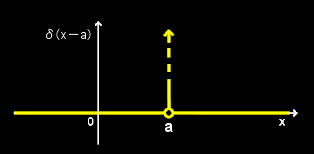δ(x-a)，またはδ(x=a)と書くこともありますが，この場合，x-a＝0　においてδ(x-a)＝∞となります。

厳密には，超関数として定義します。　　⇒[#]

［２］   これを満たす具体的な関数形を示しておきます。

［３］　指数関数型２に対するコメントを少し付け加えておきます。

δ(x−x’)＝		1		exp［i k(x−x’)］dk
		2π

これは、フーリエ変換、逆フーリエ変換の公式：

F(k) 　＝	1		f(x)・exp ［−i kx ] dx   ［フーリエ変換］
	2π

f(x) ＝	1		F(k)・exp ［i kx ] dk   ［逆フーリエ変換 ］
	2π

において、

F(k)＝		1	exp［-i kx’］　(平面波)：　および， f(x) ＝ δ(x−x’)
		2π

としたものです。　　物理的な意味はこちら　⇒　[#]

とくに，x’＝0 のとき，

δ(x)＝ 1 exp［i kx］dk 2π

および，

F(k)＝		1	フーリエ変換を上のように定義した場合
		2π

［４］

［５］　３次元での性質：

Δ		1	＝ −4πδ(r −r ’)＝−4πδ(x−x’)δ(x−x’)δ(x−x’)
		｜r −r ’｜

２次元のδ関数：回転対称
３次元のδ関数：球対称

両辺を全空間で積分すると、

a＝β　⇒	a	＝	β	＋cδ(x)
	x		x

*****

	d(logx)	＝	1	−iπδ(x)
	dx		x

ブラケット

＜x｜x’＞＝δ(x−x’)
＜x｜f(x)｜x’＞＝f(x)δ(x−x’)

２．（単位）階段関数（ヘビサイド関数）

［１］

定義：

η(x−a) ≡		δ(x’−a)dx’ ＝		0      x　＜ a
				1　　 x　 ≧ a

これを微分して、(説明はルベーグ積分のところで⇒[#])

d	η(x−a) ＝ δ(x−a)
dx

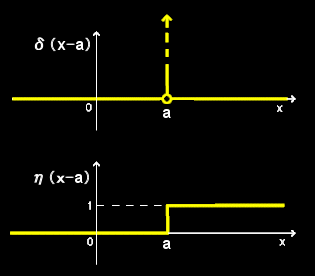
η(a)＝1/2とすることもある。記号として，ηではなく，Hを使うことも多い。

３．フーリエ変換　(可測関数)

f(t)	F(ω) ＝  f(t)・exp ［−i ωt ] dｔ　≡F [f]
1	2πδ(ω)
δ(t)	1
δ(t−τ)	exp(-iωτ)
η(t)	πδ(ω)＋PV 1 iω
δ(n)(t) = dnδ(t) dtn	(iω)n
tn	2π (-i)n dnδ(ω) dωn
exp(-iω0τ)	2πδ(ω-ω0)
cosω0t	π{δ(ω-ω0)＋δ(ω＋ω0)}
sinω0t	-iπ{δ(ω-ω0)−δ(ω＋ω0)}
η(t)cosω0t	π {δ(ω-ω0)＋δ(ω＋ω0)}＋ iω 2 (ω-ω0)2

この公式は，t→x，　ω→k　とした方がなじみある人も多いかもしれません。

公式として記憶しても用はなしますが，きちんと理解するには，超関数を「汎関数」と認識（理解）したうえで，テスト関数として急減少関数を仮定していることも心に留めておく必要があります。

例として，上の中から，階段関数ηのフーリエ変換を計算してみます。

η(t)のフーリエ変換

η(t)に小さな正数εを用いた，η（t）e^-εt　をフーリエ変換してからε→0　とする戦略をとります。まず，

F [η(t)e-εt ]＝		η(t)e-εt e-iωt dt＝			e-(ε+iω)tdt＝	1
						ε＋iω

までは問題なく計算できるはずですが，さらに超関数の極限の意味で，

F [η(t)]　＝		F [η(t)e-εt ]＝		1		＝PV	1	−iπ δ(x)
				ε＋iω			x

とできればいいのですが，この極限が正当化されるためには，

f_n　→　f　　のとき，　F [f_n ]　→　F [f ]

が成り立つ必要があります。すなわち，（次の内積について）

＜F [f_n ]，φ＞　→　＜F [f ]，φ＞

　　　　　　　　　　　　↓↑　　

＜ f_n ，F [φ]＞　→　＜ f ，F [φ]＞　　　←超関数のフーリエ変換の定義

この２行目の式では，テスト関数のフーリエ変換が再びテスト関数である必要がありますが，この要件を満たすためには，

φ∈S　［急減少関数］

にとる（制限する）必要があります。急減少関数とは，|t|→∞で，φ(t)とこのすべての導関数が|t|のマイナスのベキより速く０に近づくC^∞級関数のことです。

このS上の連続線形汎関数を緩増加超関数といい，ざっくりと，「フーリエ変換が可能な関数の集合」　となります。

よって，η（t）e^-εt　が緩増加超関数であることを示すことで，先の「＝」は正しいことになり，公式の証明は完成します。

他の公式の導出など詳細な説明は，「ルベーグ積分」の応用編で述べます。

［目次へ］

以下，追加項目のメモ

関数f(x)，g(x)に対して内積＜f，ｇ＞が定義できるとき，その一方　(普通は左側に書くf ) 　を一つ固定すると，それは汎関数Fを定義します。

変数に相当する関数をφ(x)∈D　，固定した関数をf(x)とすれば，

φ(x)	→	<f，φ＞
関数	F	スカラー

F：　　F_f(φ)＝<f，φ＞

超関数とは，Dを定義域とする（連続な線形）汎関数　F_f(φ)　のことを言います。　←連続の条件ははずすこともできる。

ベクトル空間で双対空間を考えたとき[#]と同様に，F_f(φ)∈D’　とするとき，D とD’は同型対応があり，F_f(φ)∈D’とf(x）∈D を同一視する[#]こともできます。

したがって，f(x)を超関数と呼ぶ場合もあります（あまり推奨はできない）が，このf(x)は記号とみなすべきものでいわゆる関数ではありません。

応用上重要な例では，内積は，積分，

＜f(x),φ(x)＞＝		f(x)φ(x)dx

によって定義されます。D はこの積分の値が定まる範囲内で定めます。また，積分はルベーグ積分として考えます。（そうしないと前述の同型対応とならない。）

上記の積分で内積を導入した場合，もっとも簡単な超関数は，f(x)＝1 としてえられる汎関数，

F1(φ）＝		φ(x)dx

です。（　f(x)＝1　が超関数だど主張しているのではなく，f(x)＝1によって定められる上の汎関数 F₁(φ） が超関数です。）

この場合，φ(x)の定義域Dは（-∞，∞）での積分が収束するように選ばれてなければいけません。しかし，f(x)＝1は（-∞，∞）で積分が発散してもかまいません。

一般的に，f(x)の方は局所可積分な関数であれはいいのです。テスト関数φ(x)は±∞では0です。

一方，δ関数は，φ(x)∈D　において，

＜δ，φ＞＝φ(0)

を満足する線形汎関数として定義したものです。

-------------------------------------------------------------------------------

超関数の微分の定義

一般に，f(x)がC¹級の関数，φ(x)∈D　がテスト関数であるならば，

		f ’(x)φ(x)dx　＝[f(x)φ(x)]	+∞	−		f(x)φ’(x)dx
			-∞

　　　　　　　　　　　　　　　↓　　φ(±∞)＝0

＝−		f(x)φ’(x)dx

そこで，超関数に対しても，

Ff ’(φ)　＝＜f ’(x),φ(x)＞　＝−		f(x)φ’(x)dx　＝−＜f(x),φ’(x)＞

と定義します。

さらに，φ⁽ⁿ⁾(x)∈D　となるようにφを定めておけば，n階微分も定義ができて，

n階微分

f(n)(x)φ(x)dx＝＜f(n)(x),φ(x)＞＝　(-1)n＜f(x),φ(n)(x)＞

となります。これより，

デルタ関数のｎ階微分は，

δ(n)(x−a)φ(x)dx＝(-1)nφ(n)(a)

のような性質をもつ。

超関数の極限の定義

超関数の列を　f₁，f₂，････，∈D’　とするとき，任意のφ∈D，に対して，

＜fn,φ(x)＞ ＝＜f，φ＞

⇔

fn＝ f

であるとき，超関数の列　f_n　は f に （超関数の意味で） 収束するといいます。

収束条件：関数Fn(x)，f(x)が局所可積分関数であり，収束は一様収束，平均収束すること。

例　超関数の意味で，

		1	＝PV	1	−iπ δ(x)　　　　　　　PV：コーシーの主値積分
		x＋ih		x

ヒント，

1	＝	x	−i	h	として項別にテスト関数と積を積分して極限を取れ。
x＋ih		x2＋h2		x2＋h2

デルタ列の定義

関数列f_n(x)が定める超関数の列がデルタ関数に（超関数の意味で）収束するとき，すなわち，

fn(x)＝δ(x)

であるとき，関数列をδ列（デルタ列）という。

例

δ(x)＝			n π		exp(−nx2)
			δ列

-------------------------------------------------------------------------------------------

階段関数の微分

		η’(x−a)φ(x)dx	＝［・・・］−		η(x−a)φ’(x)dx

＝−		φ’(t)dt＝−(0−φ(a))

                                 ＝φ(a)　　　　　　←η’(x−a)はδ関数と同じ働き

すなわち，

d η(x−a) ＝η’(x−a)＝ δ(x−a) dx

であることがわかります。

SUSTAINABLE　TOKIWADAIGAK　SINCE　2002