| A4 拡散方程式の導出 |
||
| f-denshi.com 更新日: | ||
[1] 水中に一滴のインクを静かに落とせば,インクは時間とともに水中全体に広がって,やがて均一に薄まります。このような現象は拡散現象と呼ばれます。これはインクに含まれている微小粒子が水(溶媒)や微小粒子どおし衝突を繰り返しながら,ランダムに熱運動し,水中全体に広がっていくためです。この現象を巨視的に記述する数学的方法(=微分方程式)を見つけましょう。
これを1次元の問題として扱います。
x軸の原点に落とされた非常に多数の粒子(←インクと思ってください)が時間とともに消滅も生成もすることなく正負両方向にx軸に沿ってランダムな運動によって広がっていく様子を考えます。ある時刻 t に形成されている x 軸に沿っての粒子の濃度分布をC(x,t)としましょう。そして,その時刻からごく短い時間Δt 経過したときに粒子の濃度分布が C(x,t+Δt) に変化したとします。まず,この2つの時刻における濃度分布の関係を導きます。
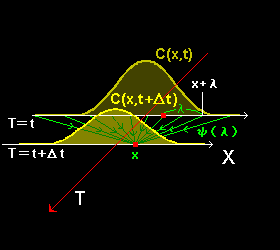 [2] 時刻 t+Δt に,位置 X=x にいる粒子は,Δt前の時刻 t にも x
軸上のどこかにいたはずです。その位置を,x+λ と書くと,λが−∞から+∞までの各位置から位置
x へ粒子はやってきたはずで,その総和が時刻 t+Δt に位置 x にいる粒子の数を与えるはずです。
[2] 時刻 t+Δt に,位置 X=x にいる粒子は,Δt前の時刻 t にも x
軸上のどこかにいたはずです。その位置を,x+λ と書くと,λが−∞から+∞までの各位置から位置
x へ粒子はやってきたはずで,その総和が時刻 t+Δt に位置 x にいる粒子の数を与えるはずです。
そこで,ある時刻に位置 x+λにいた粒子が,Δt後に位置xにいる確率をψ(λ)とすると,
| C(x,t+Δt)= | C(x+λ,t)ψ(λ)dλ ・・・・ (1) |
なる関係が成り立ちます。ψ(λ)についてもう少し説明を加えると,ψ(λ)は時刻 t によらない,(Δtには依存する)この系に固有の関数で,つぎの性質:
(1) ψ(λ)=ψ(−λ) (拡散の空間対称性:隅関数) (2) ψ(∞)=ψ(−∞)=0 (無限遠から到達する確率は0) (3)
ψ(λ)dλ=1 (確率としての規格化条件)
をψ(λ)に要求することは妥当だと考えられます。
[3] さて,次に(1)式の左辺を t のまわりにテーラー展開すると,
左辺 ≒ C(x,t)+ ∂C(x,t) Δt ∂t
一方,(1)の右辺を x のまわりに2次の項までテーラー展開して,
| 右辺 ≒ | C(x,t)+ | ∂C(x,t) | λ+ | ∂2C(x,t) | (λ2/2) | ψ(λ)dλ | |||
| ∂x | ∂x2 |
| =C(x,t) | ψ(λ)dλ+ | ∂C(x,t) | λψ(λ)dλ+ | ∂2C(x,t) | (λ2/2) | ψ(λ)dλ | |||
| ∂x | ∂x2 |
↓ (1),(3)を用いて,
| =C(x,t)+ | (λ2/2) | ψ(λ)dλ・ | ∂2C(x,t) | |
| ∂x2 |
[4] したがって,この右辺,左辺の展開式を等しいとして,
∂C(x,t) Δt = (λ2/2) ψ(λ)dλ・ ∂2C(x,t) ∂t ∂x2
を得ます。ここで,
D = 1 λ2・ψ(λ)dλ 2Δt
とおけば,
∂C(x,t) = D・ ∂2C(x,t) ∂t ∂x2
が得られますが,これを拡散方程式といいます。また,D を拡散係数と言います。
 [1] 物質が生成・消滅をしない系の濃度分布の時間変化について成り立つ重要な性質に連続の方程式(または連続の式)と呼ばれるものがあります。これは,ある時間経過したのちの微小体積中の粒子数の増加はその経過時間中にそこに入り込んだ粒子数から出て行った粒子数を差し引いた数であるという事実を方程式で表したものです。
[1] 物質が生成・消滅をしない系の濃度分布の時間変化について成り立つ重要な性質に連続の方程式(または連続の式)と呼ばれるものがあります。これは,ある時間経過したのちの微小体積中の粒子数の増加はその経過時間中にそこに入り込んだ粒子数から出て行った粒子数を差し引いた数であるという事実を方程式で表したものです。
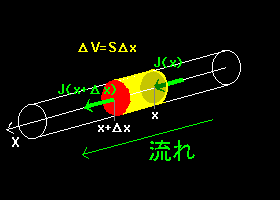
[2] 図の微小体積中の時刻tとt+Δtとの粒子数の変化量(増加分)を2通りの方法で計算します。粒子はx軸方向だけ移動可能とします。
第一の方法は,直接的な
C(x,t+Δt)SΔx−C(x,t)SΔx= ∂C(x,t) Δt・SΔx ∂t
[3] もうひとつの方法は,流入,流出量の差で,時刻tにおける位置xの流束(単位時間に単位面積をxの正方向に横切る正味の粒子数)をJ(x,t)とすれば,
微小体積への流入量 = J(x,t)SΔt
微小体積からの流出量 = J(x+Δx,t)SΔt
なので,
J(x,t)SΔt−J(x+Δx,t)SΔt=− ∂J(x,t) Δx・SΔt ∂x
[4] この2結果が等しいとおいて SΔx・Δt で割れば,連続の方程式と呼ばれる,
∂C(x,t) =− ∂J(x,t) ∂t ∂x
が成り立ちます。
[5] 拡散方程式と連続の式からフィックの法則が導かれます。
Fickの第一法則
−J(x,t)= D・ ∂C(x,t) [ Fickの第一法則 ] ∂x