 |
9 カイ二乗分布 |
| f-denshi.com 最終更新日: 11/08/25 (仮) |
| サイト検索 |
1.カイ二乗分布
[1] これまでに母集団から無作為に復元抽出した標本平均値は,標本の大きさが十分大きければ正規分布に従って分布すると考えてよいことを述べた。では,標本分散値はどのような分布に従うのであろうか。確率変数を標準化して取り扱うならば,それはカイ二乗分布と呼ばれる次の分布に従うことが示される。
|
カイ二乗分布 (χ2分布)
X1,・・・,Xnが独立に標準正規分布N(0,1)に従うとき,Z=X12+・・・+Xn2が従う分布を自由度nのカイ二乗分布という。
カイ二乗分布の確率密度関数は,
| f(z)= |
1 |
zn/2-1e−z/2 ・・・ [*] |
|
| 2n/2Γ(n/2) |
とガンマ関数[#]を用いて与えられる。
|
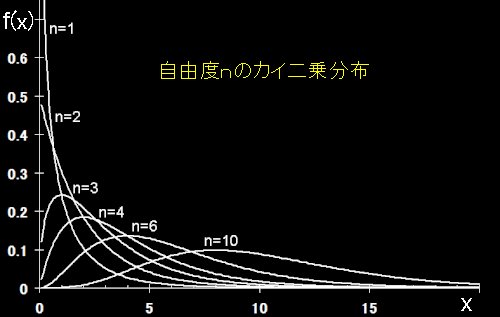
標準正規分布に独立に従うn個の確率変数をそれぞれ二乗して足し合わせて作られる確率変数,Z=X12+・・・+Xn2 の従う分布を自由度nのカイ二乗分布という。これは標本分散値の分布,すなわち,標本分散値が「標本値のバラツキ」を示す量と考えれば,「標本値のバラツキ」がいろいろな標本ごとにどのようにバラツくかを示している”理想極限的”分布ということができる。
たとえば,人口1億人の中から全日本経済新聞社がある1000人のグループを選び出し,この大きさ1000の標本についての身長を調べ,その標本の標本平均値,標本分散値を計算することができるだろう。一方,フジエダ電子出版社も負けずに無作為に別途,1000人のグループを選び出し,同様な計算を行うこともできる(ホントか?)が,その標本平均値,標本分散値は先のものとは一般的には異なる。さらに別のシンクタンクも大きさ1000の標本を選び出し,統計値を同様に算出することができるであろう。そのとき,様々な調査機関が算出した標本平均値,および,標本分散値はいずれも変数を標準化[#]してプロットしていけば,標準正規分布,および,カイ二乗分布が現われるのである。そのような意味で,カイ二乗分布は正規分布と並ぶ重要な統計分布ということができる。
[2] 前者(=標準正規分布)はすでに中心極限定理として説明済みなので,ここではカイ二乗分布について解説する。まず,題意の確率密度関数が[*]で与えられることを示したいが,n=2の場合から調べていこう。
Xが標準正規分布にしたがうとき,その2乗,すなわち,Y=X2 が従う分布を求める。最初にXの従う確率密度関数は,
| f(x)=N(0,1)≡ |
1 |
exp |
 |
−x2 |
 |
|
|
|
|
|
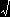 |
2π |
|
|
2 |
であることを思い出さなければならない。Y=X2 であるとき,Y≦y となる確率は,
|
|
|
|
|
|
|
| P(Y≦y)=P(− |
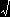 |
y |
≦X≦ |
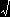 |
y |
) |
に対応することに注意すると,Yの確率分布関数は,
| F(y)= |
 |
|
|
|
| + |
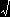 |
y |
|
f(x)dx = 2 |
 |
|
|
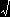 |
y |
|
f(x)dx |
|
|
|
|
|
| - |
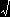 |
y |
|
0 |
|
|
|
|
| で与えられる。さらに,変数変換:y=x2,dy=2xdx=2 |
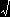 |
y |
dx をおこなって, |
| F(y)= |
 |
y |
| 1 |
|
|
|
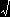 |
2πy |
|
|
exp |
 |
−y |
 |
dy |
|
|
| 0 |
2 |
したがって,Yの従うべき確率密度関数はこの被積分関数,
である。
[2] 次に2つの確率変数 X1,X2 が独立に標準正規分布に従い,Y1=X12,Y2=X22 とおいたとき,Z=Y1+Y2 の従う確率密度関数を求める。そのためには確率変数の和がそれらが従う分布のたたみ込みで与えられることを思い出す必要がある[#]。
すると, 確率変数Y1,Y2 双方とも確率密度関数 h1(y)に従うときは,z=y1+y2 ,y1,y2≧0,z≧0 に注意して,たたみ込み,
| h2(z)= |
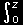 |
h1(y)h1(z-y)dy |
|
|
を計算すれば,確率変数,Z=Y1+Y2 (=X12+X22) の従う確率分布が求まるはずである。以下計算を進めると,
| h2(z)= |
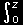 |
1 |
exp |
 |
−y |
 |
・ |
1 |
exp |
 |
−(z−y) |
 |
dy |
|
|
|
|
|
|
|
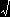 |
2πy |
|
|
2 |
|
|
|
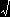 |
2π(z−y) |
|
|
2 |
y=uzと変数変換して, dy=zdu
| = |
1 |
exp |
 |
−z |
 |
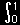 |
1 |
du |
|
|
|
| 2π |
2 |
|
|
|
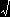 |
u(1−u) |
|
|
ここで,uに関する積分値=π(u→sin2θと変数変換して計算せよ)なので,
| h2(z)= |
1 |
exp |
 |
−z |
 |
|
|
| 2 |
2 |
|
でなければならないことがわかる。
[3] 次に一般化して,n個の独立に標準正規分布に従う確率変数Xiの和から作られる確率変数,Z=X12+・・・+Xn2の従う確率密度関数hn(z)を求めたいのであるが,n=1,2の場合の結果を参考にして,適当な係数cnを用いて,
| hn(z)=cnzn/2-1・ |
exp |
 |
−z |
 |
・・・・ [1] |
|
| 2 |
と仮定して,具体的にcnを定めてやることを考える。それは,n-1のとき成り立っている仮定して,h1からh2を求めたときと同様のたたみ込みの積分を実行してみると,
| hn(z)= |
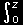 |
hn-1(y)h1(z-y)dy |
|
|
| hn(z)= |
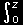 |
cn-1y(n-1)/2-1・exp |
 |
-y |
 |
・ |
c1(z−y)1/2-1exp |
 |
−(z−y) |
 |
dy |
|
|
| 2 |
2 |
| =cn-1c1 |
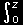 |
y(n-3)/2(z−y)-1/2dy |
・exp |
 |
−z |
 |
|
| 2 |
↓ y=uzと変数変換して, dy=zdu
| = |
 |
cn-1c1 |
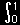 |
u(n-3)/2 |
du |
 |
zn/2-1・exp |
 |
−z |
 |
・・・[2] |
|
|
|
|
|
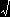 |
(1−u) |
|
|
2 |
となる。ここで,[1]と[2]とを比較すると,
| cn= |
 |
cn-1c1 |
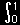 |
u(n-3)/2 |
du |
 |
|
|
|
|
|
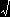 |
(1−u) |
|
|
とおけば,hn(z)は[1]の形で表される。すでに示したように,n=1,2のときhn(z)は[1]の形で表されるので,数学的帰納法により任意のnに対して[1]と書けることがわかった。
[4] 一方,hn(z)は確率密度の意味を持つので,cnは
 |
hn(z)dz=1 |
を満たしているはず。したがって,
| cn |
 |
zn/2-1・e-z/2dz=1 |
|
|
z=2tとおくと,
| 2n/2cn |
 |
tn/2-1・e-tdt=1 |
|
|
| ∴ cn= |
1 |
|
| 2n/2 |
 |
tn/2-1・e-tdt |
|
|
|
とcnを表すことも可能である。さらに,ガンマ関数[#],
| Γ(s)= |
 |
ts-1・e-tdt |
|
|
であることを思い出すと,
となる。
[5] 以上で,独立に標準正規分布に従う確率変数,X1,X2,・・・,Xn から作られる確率変数,Z=X12+X22+・・・+Xn2 が従う確率密度関数は,
| hn(z)= |
zn/2-1 |
exp |
 |
−z |
 |
|
|
| 2n/2Γ(n/2) |
2 |
|
で与えられることが証明された。この確率密度関数をもつ確率分布を「自由度nのカイ2乗分布(χ2分布)」という。
この1階微分から,n≧3のとき,z=n-2においてhn(z)は最大値をとることがわかる。また,
平均(期待)値: n,
分散: 2n
である(演習)。
2.標本分散の自由度
標本分散をカイ二乗分布に帰着させる種々の統計解析において,次の定理は大変重要である。
|
定理
Xiが独立に正規分布にしたがうとき,標本平均と標本分散 (または不偏分散),
| X~= |
 |
Xi |
|
| n |
| S2= |
 |
(Xi−X~)2 |
または, |
s2= |
 |
(Xi−X~)2 |
|
|
| n |
n−1 |
は互いに独立であり,nS2/σ2 (または(n-1)s2/σ2) は自由度n−1のカイ二乗分布に従う。
|
証明
[1] まず,次の確率変数変換を行う。
ここで,Xiが独立に正規分布(μ,σ)にしたがうならば,Yiは独立に標準正規分布N(0,1)に従う。さらに,Yiを成分とするベクトルは正規直交基底を正規直交基底に移す直交行列を用いて次のような基底変換を行うと,
| Y = |
 |
Y1 |
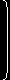 |
Z=UY
⇒ |
Z = |
 |
Z1 |
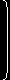 |
| Y2 |
Z2 |
| : |
: |
| Yn |
Zn |
この変換(=広義の座標軸の回転に相当する)後のベクトルZの成分Ziも独立に標準正規分布N(0,1)に従う[#]。また,ベクトルの大きさは不変に保たれ,その成分については,
Y12+Y22+・・・+Yn2 = Z12+Z22+・・・+Zn2
が成り立つ。このとき,横ベクトルuiを用いて直交行列を,
| U = |
 |
u1 |
 |
|
| u2 |
| : |
| un |
と書くとき,1行目を
| u1= |
1 |
(1,1,・・・,1) |
|
|
|
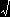 |
n |
|
と選び,引き続き,{u1・・・,un}が正規直交基底となるようu2,・・・,unを順に選んでいけば,直交行列Uを定めることができる[#]。そのとき,第1番目(1行目)の成分は,
| Z1=u1・Y = |
1 |
(Y1+Y2+・・・+Yn) |
|
|
|
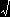 |
n |
|
| = |
1 |
・ |
1 |
(X1+X2+・・・+Xn−nμ) |
= |
|
|
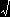 |
n |
|
(X~−μ) |
|
|
|
|
|
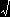 |
n |
|
σ |
σ |
と変形することができる。(Z1は正規分布N(μ,σ2/n)に従う。) よって,
| ∴ Z12= |
n |
(X~−μ)2 ・・・・(3) |
|
| σ2 |
と書ける。すると,
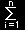 |
Yi2= |
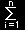 |
(Xi−μ)2 |
|
| σ2 |
| = |
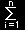 |
{(Xi−X~)+((X~−μ)}2 |
|
| σ2 |
| = |
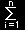 |
(Xi−X~)2 |
+2(X~−μ) |
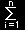 |
Xi−X~ |
+ |
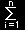 |
(X~−μ)2 |
|
|
|
| σ2 |
σ2 |
σ2 |
最後の=のところでは,標本分散S2の定義と(3)を用いた。
| ここで, |
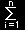 |
Yi2 |
は Z12+Z22+・・・+Zn2 と等しいことを思い出せば,最後の式は, |
|
|
であることを示している。結局,適当な基底変換Uによって,確率変数,
「 X~は,Z1のみ,nS2/σ2はZ22+・・・+Zn2に従う。 」
ようにすることができると述べることができ,また,Ziが独立にN(0,1)に従うことから,Z12とZ22+・・・+Zn2も独立。つまり,「X~とnS2/σ2は独立で,X~は正規分布N(μ,σ2/n),そして,nS2/σ2は自由度n-1のカイ二乗分布に従う」と述べることが可能である。
3.カイ二乗分布の積率母関数
計算:
確率密度関数が
| f(x)= |
1 |
xn/2-1e−x/2 |
|
| 2n/2Γ(n/2) |
であることから,
| M(t)= |
 |
etx |
| 1 |
xn/2-1e−x/2 dx |
|
| 2n/2Γ(n/2) |
|
|
|
| = |
|
 |
xn/2-1e-{(1−2t)/2}x dx |
|
|
| = |
1 |
・ |
Γ(n/2) |
|
|
| 2n/2Γ(n/2) |
{(1−2t)/2}n/2 |
途中で公式,(a=n/2として)
 |
xs-1e−ax dx= |
Γ(s) |
|
| as |
を用いた。
つづく,・・・たぶん。
[目次]
