4　多様体上の微分
f-denshi.com   ［目次へ］　 最終更新日：22/09/19　　　　校正中　
サイト検索


１．Cr級写像 f ： M → N の微分

［１］　Cr級の m次元多様体 M から n次元多様体 N  への写像，

f ： M → N　　　　　

を Cr級写像とします。

M上のCr級曲線 c(t)：（-ε,ε）→ M，および，写像 f  によって写された N上の曲線

fοc(t) ： （-ε,ε）→ N，

ただし，

c(t)　　＝( x1(t)，x2(t)，…xm(t) )
fοc(t) ＝（ y1(t)，y2(t)，…yn(t) ）
　　　　＝( f1(x1(t)，x2(t)，…xm(t))， f2(x1(t)，x2(t)，…xm(t))，
　　　　　　　　　　　　　　　　　・・・　　，fn(x1(t)，x2(t)，…xm(t)) )

は  t＝tp において，

c(tp)　 ＝p　　　　
fοc(tp)＝q

を満たすとします。

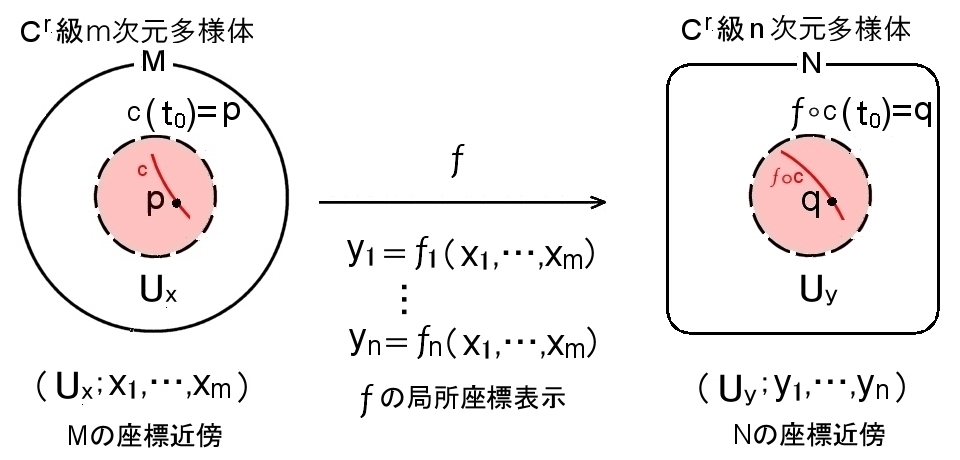
ここで，p を含む座標近傍は （Ux，x1,x2,…,xm) ，q を含む座標近傍を（Uy，y1,y2,…,ym) とし，写像 f の局所座標表示は，

y1 ＝f1(x1,x2,…,xm)
y2 ＝f2(x1,x2,…,xm)
   …  
yn ＝fn (x1,x2,…,xm)		 　　　　　　　　　　　･･･　(3)

としています。

［２］　この表記の下で次の命題です。

命題　　速度ベクトル [#] 間の写像　

対応する M上，N上の速度ベクトルをそれぞれ，　( q＝f(p) として )

dc(t) tp ＝u1 ∂ p ＋u2 ∂ p …＋um ∂ p ∈Tp(M)
d t ∂x1 ∂x2 ∂xm
　 d(fοc(t)) tp ＝w1 ∂ q ＋w2 ∂ q …＋wn ∂ q ∈Tq(N)
d t ∂y1 ∂y2 ∂yn

と係数の組，u1，u2，…，um　および，w1，w2，…，wn　を用いて書くとき，これら係数の間には，

wj＝ ∂fj (p) uk    ・・・　[*]　
∂xk

という関係がある。行列を用いて書くと，

w1
：
：
：
：
wn
＝
∂f1 (p) ∂f1 (p) … ∂f1 (p)
∂x1 ∂x2 ∂xm
u1
：
：
：
：
um
 　… [*] ’
：
：
∂fn (p) ∂fn (p) … ∂fn (p)
∂x1 ∂x2 ∂xm

なお，この行列を写像 f のヤコビ行列といい，(Ｊf)p と書く。
(初等解析学の積分変数の変換の式 [#] と同形，
教科書によっては行と列を入れ換えて記述することもある。)
uk⇔ dxk (tp) ，　wk⇔ dyk (tp) 　　と対応している。
dt dt

[*] の証明　　　　　

wj ∂ q 　　　　　　　＝ d( fοc(t)) tp [N上の速度ベクトル]
∂yj d t
↓　　　前ページの速度ベクトル［☆☆］式同様　[#]
＝ dyj (tp) ∂ q
dt ∂yj
　　↓　　　(3)　式より
＝ d fj (x1(t),x2(t),…,xm(t)) (tp) ∂ q
dt ∂yj
＝ ∂fj (p) dxk (tp) ∂ q
∂xk d t ∂yj
 　↓　　　前ページの［☆☆］式　[#]
＝ ∂fj (p) uk ∂ q
∂xk ∂yj
wj

この式と最初と最後を比較して，

wj＝ ∂fj (p) uk    ・・・　[*]　
∂xk

［３］

命題

多様体M上の接ベクトル空間 Tp(M) に属する任意のベクトルu に対して，p を通る Cr級曲線
c(t)： （-ε，ε）→ M　　；　c(tp)＝p

が存在して，

dc(t) tp ＝u
d t
となる。言い換えると，M上の任意の点 p における任意の接線ベクトルに等しくなるような，速度ベクトルをもつ曲線 c が必ず存在する。

具体的には，任意のベクトルが，

u＝u1 ∂ p ＋u2 ∂ p …＋um ∂ p ∈Tp(M)
∂x1 ∂x2 ∂xm

および，p の局所座標を (p1，p2，…，pm) であれば，

c(t)＝ (p1＋u1t，p2＋u2t，…，pm＋umt)

とすればよいことが分かります。

［４］　これらの２つの命題から次のように微分を定義することができます。

定義  微分

接ベクトル空間 Tp(M) の元を接ベクトル空間 Tf(p)(N) の元に対応させる線形写像を，
(df)p： 　u ＝ dc(t) tp →　w ＝ d( fοc(t)) tp
d t d t
↑ ↑
∈Tp(M) ∈Tf(p)(N)

と書いて，p における写像 f ： M → N の微分と呼び，(df)p と書く。

(df)p の行列表現が [*] ’で示したヤコビアン(Ｊf)p である。

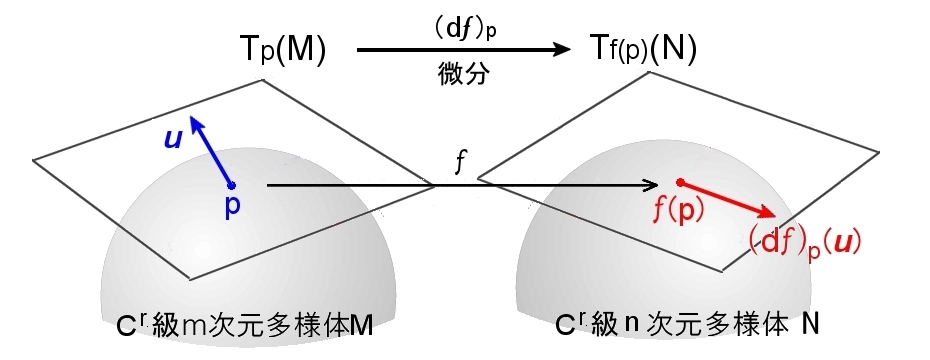
すると，[*]’ 式を用いて，

w ＝ (df)p(u ) ⇔
w1
：
：
：
：
wn
 ＝ (Jf)p
u1
：
：
：
：
um
ヤコビ行列で表記

と成分で記述することができます。

特に，u が Tp(M) の基底をなす r 番目のベクトル ∂ p であるとき，
∂xr
wj＝ ∂fj (p)  
∂xr

であるから，( [*]’で，uk＝1 (k＝r)，uk＝0 (k≠r)　とする。）

w ＝ w1 ∂ q ＋w2 ∂ q …＋wn ∂ q
∂y1 ∂y2 ∂yn
　　＝ ∂fj (p) ∂ q
∂xr ∂yj

［５］　したがって，次の公式が得られます。

公式１

Cr級多様体 M から Cr級多様体 N への写像 f の局所座標表示が

y1 ＝f1(x1,x2,…,xm)
   …  
yn ＝fn (x1,x2,…,xm)
であるとき，
(df)p ∂ p ＝ ∂fj (p) ∂ q 　　　　　　・・・　(4)　　
∂xr ∂xr ∂yj

が成り立つ。

このように表記すれば，(df)p が f の微分と呼ばれる理由に納得がいきますね。



［６］　いくつか公式を列挙します。

公式２

Cr級多様体 M から Cr級多様体 N への写像を f とする。p∈M　における任意の接ベクトル u ∈Tp(M) と f(p) ∈N の周りで定義された Cr級関数 h について，

u (hοf)＝[(df)p(u)] (h)

が成り立つ。

この公式の意味は下図を参考にしてください。



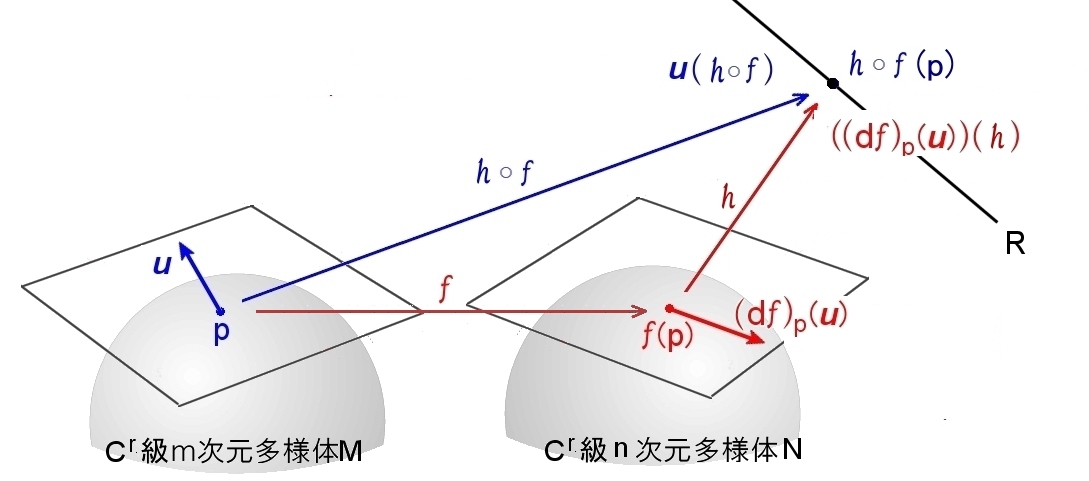
（u ，および，(df)p(u) を汎関数(方向微分作用素(演算子))とみなして，
左辺は，hοf に，右辺は h に作用させている。）

証明

dc(t) tp ＝u　とすると　[#]　，
d t

微分の定義 [#] から

(df)p (u)＝　 d(f οc(t)) tp
d t

一方，前ページの速度ベクトルの定義 [**]より [#]，

u (h)＝ d h(c(t)) tp ≡ d c(t) tp (h)　　(2)
d t dt

と表せる。この２式を用いて，

[(df)p (u)](h)　＝　 d (f ο c(t)) tp (h)
d t
＝ d h(fοc(t)) tp ＝ d (hοfοc(t)) tp
dt dt
＝ d (h οf) (c(t)) tp
dt
＝　 d c(t) tp (h οf)
d t
　　↓　(2)
＝u (hοf)　　　　　　　　　終


［７］　多様体 M，N のいずれかが１次元の場合の公式は次のとおりです。

公式３

（１）　f ： Rm→R　；　Tp(Rm)→Tf(p)(R)　　（Rの局所座標を y とする）

(df)p(u)＝u (f) d f(p)
dy

（２）　c ： R→Rm ；　Tt(R)→Tc(t)(Rm)　　　
　　　　c(t)　＝( x1(t)，x2(t)，…xm(t) )　　（Rの局所座標を t とする）

(dc)t d t ＝ dxk (t) ・ ∂ c(t)
dt dt ∂xk

が成り立つ。

証明

（１）　N が1次元の場合です。

u ＝ uk ∂ p
∂xk

とすると，このベクトルが前ページ [#]，

vc( f ) ＝ dxk (tp) ∂f ( p )　　　　・・・　　　［☆］　
dt ∂xk

と同様な関係が成り立つことをから，

u (f) ＝ dxk (tp) ∂f ( p ) ＝ uk ∂f ( p )
dt ∂xk ∂xk

が成り立っている。これらを用いると，

(df)p(u) ＝ (df)p uk ∂ p
∂xk
　　　　↓　線形性
　　　＝ uk (df)p ∂ p
∂xk
　　　　↓　公式１ で，Σの和を j =1のみ(1次元)とし，
           　　　 fj→f　，yj→y ，q→f(p) と書く
　　　＝ uk ∂f (p) d f(p)
∂xk dy
　　　＝ uk ∂f (p) d f(p)
∂xk dy
　　　＝ u (f) d f(p) 　　　←Rの局所座標が t　　
dy
f の方向微分 基底

と変形することができる。

左辺のu ＝点 p の接ベクトル
　　　↓　の微分 (df) をとったものは，　
右辺のu ＝fの方向微分×（Rの基底）に等しい。

という意味になっています。

（２）　　M が１次元の場合です。　←関数 c は N 上に曲線を与えています。

c ： R→Rm ；　Tt(R)→Tc(t)(Rm)，c(t)＝( x1(t)，x2(t)，…xm(t) )

ということで，公式１，

(df)p ∂ p ＝ ∂fj (p) ∂ q 　　　・・・　(4)　　
∂xr ∂xr ∂yj

において，xr → t (=p点に相当)， yj ＝ fj (x1,x2,…,xm)　→　xk ＝ xk (t)，q = f(p) → c(t)　と置き換えると，

(dc)t d t ＝ dxk (t) ・ ∂ c(t) 　( ＝vc  [#] )
dt dt ∂xk

この式の意味は，微分 (dc)t によって，

Rの速度ベクトル (基底) を， Rm の曲線 c上の速度ベクトル [#] に写している

ことが分かります。

［８］

公式４　　合成写像の微分

M，N，Q を Cr級多様体とする。また，f ： M → N， g ： N → Q を Cr級写像とするとき，

(d(g οf))p＝ (dg)f(p) ο (df)p

が成り立つ。行列で表すと，

J(g οf)p＝(Jg)f(p) (Jf)p


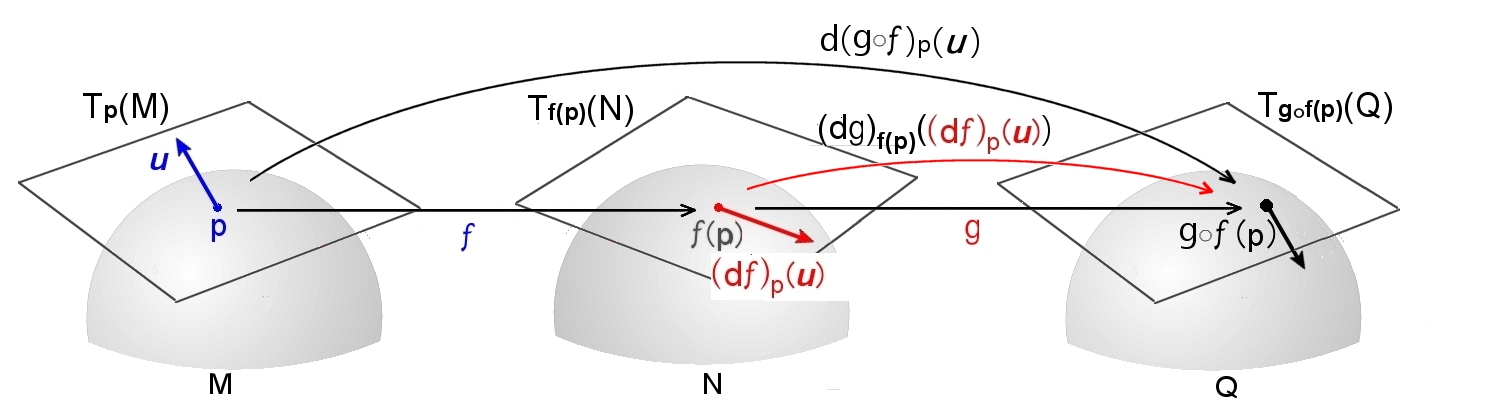
上図を参考にして，

(d(g οf))p(u)＝ (dg)f(p) [(df)p(u)]

を示せばよい。



２．　微分同相写像の性質

［１］　微分同相写像 f の定義はすでに述べています [#] が，多様体の一点 p の近傍についてだけであれば，次の条件を満たせば，微分同相写像であることが分かります。

命題　　微分同相写像

（１）　f が全単射　　　　　　　　　　　　　　　同相写像

（２）　(Jf)p が正則行列 　；  　U 〜 f(U)　微分同相

のとき，p の近傍で局所的に微分同相写像である。

(1)

［２］

補題：

(1)　多様体 M において，M，Tp(M) の恒等写像をそれぞれ IM，ITp(M) とするとき，

（d (IM))p＝ITp(M)

が成り立つ。

証明

(1)　f が恒等写像ならば，f(p)=p　であり，局所座標表示で，yj＝fj(x1,x2,…,x)＝xj　が(4)式

(df)p ∂ p ＝ ∂fj (p) ∂ q 　　　・・・　(4)　　
∂xr ∂xr ∂yj

で成り立つ。すなわち，

(d IM)p ∂ p ＝ ∂xj (p) ∂ f(p) 　　　　　
∂xr ∂xr ∂xj
　　　　　　　　　　　　　　＝ ∂ p 　　　　　
∂xr

これより，∀X ∈Tp(M)に対して，

（d (IM))p(X)＝X＝ITp(M)(X)

［３］

命題：　f： M → N がCr級微分同相写像ならば，任意の p∈M について，
(df)p： Tp(M) → Tf(p)(N)
は同型写像であって，
(df)p-1＝(df-1)f(p)
ここで，左辺は同型写像 (df)p：Tp(M)→Tf(p)(N) の逆写像。右辺は f の逆写像 f-1：N→M の f(p) における微分

証明

合成写像の微分に関する公式 [#] より

(df-1)f(p)ο(df)p＝d(f-1οf)p＝d(IM)p＝ITp(M)
(df)pο (df-1)f(p)＝d(fοf-1)f(p)＝ITf(p)(N)

を (df-1)f(p) が (df)p の逆写像 (df)p-1 であることを確かめることができる。


［５］　結局，次の命題が重要です。

命題：　微分同相による次元の不変性

Cr級微分同相写像 f ： M → N が存在すれば，

dim M＝dim N

である。



［目次へ］





命題：

(1)　m次元多様体Mの局所座標系を固定して，写像f：M→Mを考えるとき，

J(iM)＝Em　［m次正方行列］

である。

(2)　f：M → N がCr級微分同相写像，p∈M，f(p)∈N の周りの局所座標系を固定すれば，(Jf)pの逆行列は，
(Jf)p-1＝(Jf-1)f(p)